Покупка и продажа векселя с использованием простой учетной ставки

Доходность этой финансовой операции связана с разностью цен купли-продажи, которая зависит от сроков погашения векселя и уровнем учетных ставок в момент купли-продажи векселя. Обозначим S – номинал векселя, d₁ – учетная ставка, по которой его учел банк за время t₁ до его погашения. Тогда цена покупки P₁ банком равна P₁ = S (1- d₁ t₁).

Банк продал вексель за время t₂ до его погашения по ставке d₂. Цена продажи P₂ равна P₂ = S (1- d₂ t₂).

Таким образом, вексель куплен по цене P₁ и продан по цене P₂ через срок (t₁-t₂) дней. Доход от купли-продажи векселя равен P₂ - P_1.

Эффективность операции за срок (t₁-t₂) выражается в виде процентной ставки i:

i = .

Подставляя в эту формулу соответствующие значения для P₁ и P₂ получаем доходность за срок t₁-t₂

i = .

Зная доходность за (t₁-t₂) дней можно рассчитать годовую эффективную ставку простых или сложных процентов.

Пример 33.

Вексель куплен за 167 дней до его погашения, при покупке использована учетная ставка 6%. Через 40 дней его реализовали по учетной ставке 5,75%. Определить эффективность операции купли-продажи. (К=360 дней).

Решение.

Вексель куплен за 167 дней по цене P₁ .

P₁ =

За 127 дней до его погашения вексель продан по цене

P₂ =

Доходность операции за 40 дней составила

i = %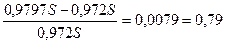

Доходность операции, выраженная годовой ставкой простых процентов равна:

i_эф = %

Доходность операции, выраженная годовой ставкой сложных процентов равна:

i_эф.сл. = %

Эти процентные ставки эквивалентны и показывают равную доходность финансовой операции.

Покупка и продажа финансового инструмента,

Приносящие проценты

При покупке-продаже финансового инструмента доход образуется за счет разницы цен купли-продажи, которые зависят от процентных ставок в момент купли-продажи. Для оценки доходности также используется эффективная процентная ставка.

Цена покупки Р₁ определяется на основе дисконтирования по процентной ставке i₁:

Р₁=S/(1+i₁t₁)

Цена продажи Р₂ определяется дисконтированием по процентной ставке i₂:

Р₂=S /(1+i₂t₂)

Доходность операции купли-продажи за срок t₁ - t₂ равна:

i = .

Зная доходность за срок (t₁ - t₂) дней можно определить годовую процентную ставку.

Пример 34.

Депозитный сертификат номиналом 100 тыс.руб., выпущенный на год с начислением простых процентов по ставке 20% годовых, куплен за 180 дней до его погашения и продан через 30 дней. Ставки простых процентов в моменты покупки и продажи составляли 12% и 10% соответственно. Определить доходность операции купли-продажи в виде эффективной ставки простых и сложных процентов

Решение.

К концу срока цена сертификата составит 100000 (1 + 0,2 · 1) = 120000 (руб.). Поскольку сертификат куплен за 180 дней до его погашения, то его цена покупки Р₁ = 120000 / (1 + 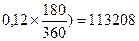(руб.)

Цена продажи равна Р₂ = 120000 / (1 + (руб.)

Доходность за 30 дней равна: i = %

Годовая ставка простых процентов i_эф. = %.

Годовая ставка сложных процентов i_эф.сл. = %.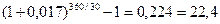

Контрольные вопросы

1. Какие виды доходов может получать банк от ссудных и учетных операций?

2. Дайте определение эффективной ставки процентов.

3. Как рассчитать годовую эффективную ставку, если известна доходность за срок финансовой операции?

4. От каких факторов зависит доходность купли-продажи финансовых инструментов?