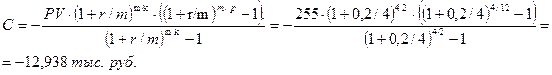ВЫПЛАТЫ p РАЗ В ГОДУ, А НАЧИСЛЕНИЕ процентов m РАЗ В ГОДУ
Определим теперь абсолютное значение наращенной суммы для наиболее общего случая: р - срочная рента с начислением процентов m раз в году.
Пусть С - это постоянная рента, начисляемая р раз в году. Число выплат ренты за k лет равно k·p. Количество начислений процентов в году равно m.
За период m/p года на каждую выплату С нарастают проценты в размере (1+  )m/p.
)m/p.
1) Если выплаты идут пренумерандо, то к концу k·p-ого периода сумма выплат составит
FV=C·(1+r/m)m/p+ C· (1+r/m)2m/p+···+ C· (1+r/m)k·p·m/p=
=C· (1+r/m)m/p· [1+ (1+r/m)m/p+···+ (1+r/m)(kp-1)·m/p].
Это сумма геометрической прогрессии с первым членом
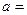 C·(1+r/m)m/p и частным q= (1+r/m)m/p.
C·(1+r/m)m/p и частным q= (1+r/m)m/p.
Она равна [7]
FV=C· (1+r/m)m/p· 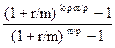 .
.
При p=m эта формула плавно переходит в (2.1).
2) Если выплаты поступают постнумерандо, то к концу k-ого года сумма выплат составит
FV=C+ C(1+r/m)m/p+···+ C(1+r/m)(kp-1)··m/p
В этом случае
FV=C 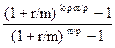 .
.
При p=m эта формула переходит в (2.2).
Обе формулы объединим в одну
FV=C 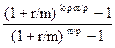 ·(1+r/m·тип)m/p. (2.15)
·(1+r/m·тип)m/p. (2.15)
тип=1 для выплат пренумерандо и тип=0 для выплат постнумерандо.
Уравнение эквивалентности приобретает вид
| |
FV+PV(1+r/m)m·k + C 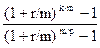 ·(1+r/m·тип)m/p =0 (2.16)
·(1+r/m·тип)m/p =0 (2.16)
Из него можно определить любые из восьми величин FV, PV, c, r, k, m, p через остальные семь.

Пример 2.9
Создается страховой фонд фирмы общей суммой 10 млн. руб. Фонд должен быть создан в течение 5 лет. Взносы в фонд производятся ежемесячно пренумерандо. Проценты начисляются ежеквартально по процентной ставке 18% годовых. Определите размер платежа и сумму, накопленную через 3 года.
|
 PV=0
PV=0
FV=10 млн. руб.
k=5
p=12
m=4
r=0,18
 |
С=? FV(k=3) =?
Через 3 года сумма фонда составит
FV3= 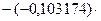
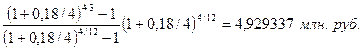
Динамика наращивания суммы фонда, рассчитанная в Excel, представлена таблицей (2.3) и графиком pис.(2.1)
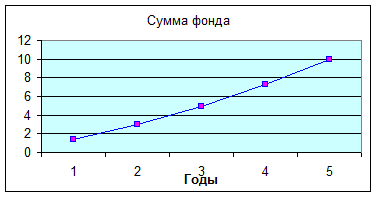
Таблица (2.3)
| Год | Сумма фонда |
| 1,363722 | |
| 2,989987 | |
| 4,929337 | |
| 7,242049 | |
Рис. 2.1
К сожалению, при p¹m для расчета величин из уравнения (2.16) не применимы финансовые функции Excel. В частности, нельзя рассчитать номинальную процентную ставку r с помощью функции НОРМА. Однако, в Пакете анализа Excel есть средство для решения нелинейного уравнения (2.16).

Пример 2.10
Фирма дала дочерней фирме в кредит 3 млн. руб. с условием возвращения долга в течение 5 лет равномерными платежами по 0,2 млн. руб. ежеквартально постнумерандо при условии начисления процентов раз в полгода. Какова эффективность этой сделки?
 Решение(с точки зрения дочерней фирме)
Решение(с точки зрения дочерней фирме)
|
FV=0
k=5
m=2
p=4
С=-0,2 млн. руб.
 r=?
r=?
Выполнение
1) Вызываем Excel.
2) В ячейку А1 помещаем число 0,1 – это первоначальное значение r.
3) В ячейке А2 набираем функцию цели:
=3*(1+A1/2)^10-0,2*((1+A1/2)^10-1)/(КОРЕНЬ(1+A1/2)-1)
Получаем величину – 0,2066
4) Сервис – Поиск решения
5) В появившемся окне Поиск решения задаем:
5.1 Установить целевую ячейку $A$2 равной ¤ значению 0, изменяя ячейки: А1
5.2 Выполнить.
Результат
В ячейке А1 появляется корень уравнения (2.17) r=0,118, в ячейке А2 – значение функции
f (r)=3,85*10-7 @ 0 - машинный нуль.
Итак, в результате решения примера выяснилось, что эффективность подобной сделки
rэфф=11,8%. Если банк может обеспечить больший процент по вкладу, то с точки зрения головной фирмы сделка не выгодна, а с точки зрения дочерней – наоборот.
ВЫБОР ИПОТЕЧНОЙ ССУДЫ
Пример 2.11 [2, 3.5] Строительная фирма предлагает клиентам в новом доме квартиры стоимостью 300 тыс. руб. с разными условиями продажи.
1) Для молодых семей – 15%-ый первый взнос авансом, а остаток стоимости выплачивается по льготному государственному кредиту в течение 20-ти лет по 5% годовых. Платежи осуществляются равными годовыми суммами в конце каждого года.
2) Аванс – 15%. Остальная сумма выплачивается в кредит сроком на 2 года по номинальной процентной ставке 20% годовых. Проценты начисляются 4 раза в год, а платежи происходят ежемесячно.
3) Аванс – 10%. Предусмотрена отсрочка платежей на один год. Оставшаяся сумма выплачивается в течение трех лет равными месячными платежами с ежемесячным начислением процентов. Номинальная процентная ставка кредита 18%.
Требуется рассчитать периодические выплаты и общую сумму выплат во всех трех случаях.
Условия и финансовые последствия вариантов 1 - 3 приведены в таблице 2.4.
Принятые обозначения:
Р – стоимость квартир;
q% - проценты от стоимости квартиры, отчисляемые в качестве аванса;
r – номинальная процентная ставка;
k – срок кредита;
t – продолжительность отсрочки;
m – число периодов начисления процентов;
p – число периодов начисления платежей;
C– величина годового платежа;
FV – общая наращенная стоимость финансовой ренты;
S - общая сумма выплат по ипотечной ссуде, включая аванс.
FVк – будущая сумма кредита к концу срока кредита во всех трех случаях равна 0.
Таблица 2.4
| № варианта | P тыс. руб. | q % | k лет | t лет | m | p | r % | C тыс. руб. | PV тыс. руб | FV тыс. руб. | S тыс. руб. |
| 20,462 | 676,591 | 721,591 | |||||||||
| 155,257 | 375,751 | 421,751 | |||||||||
| 140,047 | 551,739 | 581,739 |
Вариант1
Стоимость кредита PV=P(1 – 0,15)=255 тыс. руб.

|
r=0,05
t=0
m=1
p=1
тип=0
Сколько же выплатят наши молодожены в течение 20 лет (считаем, что выплачивать они начинают с нуля, PVв=0)? Наращенная стоимость всех платежей по формуле (2.4)
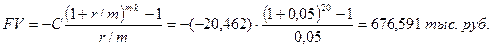
Будущее значения всех выплат по кредиту можно получить и с помощью финансовой функции
=БЗ(0,05;20;-20,462)=676,591 тыс. руб.
С учетом аванса молодожены в течение 20-ти лет должны будут выплатить сумму
S=676,591+45=721,591 тыс. руб.,
что на 421,591 тыс. руб. превышает первоначальную стоимость их квартиры.
Вариант 2

|
k=2
m=4
p=12
r=0,2
тип=0
Величина годового платежа
С= - 12,938·12= - 155,257 тыс. руб.
Наращенная стоимость финансовой ренты по формуле (2.15)


C учетом аванса владельцы квартиры должны будут вернуть строительной фирме сумму
S=367,751+45=421,751 тыс. руб.
Вариант 3
Стоимость кредита PV=P·(1-q)=300·(1-0,1)=270 тыс. руб.

|
t=1
m=12
p=12
r=0,18
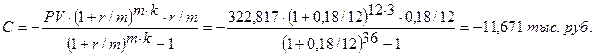
Выплаты за год
С=-11,671·12= - 140,047 тыс. руб.
Наращенная стоимость финансовой ренты за три года

С учетом аванса владельцам квартиры придется выплатить строительной фирме
S=551,739+30=581,739 тыс. руб.
Анализ вариантов показывает, чем больше срок кредита, тем большую сумму придется выплачивать владельцам квартир даже при более низкой процентной ставке.
Задачи
2.1 На счет в банке вносится ежегодно постнумерандо сумма в 5000 долларов под 5% годовых. Какая сумма окажется на счете через 10 лет?
2.2 Рассматриваются две схемы вложения денег на 5 лет: в начале каждого года под 14% годовых или в конце каждого года под 18% годовых. Какая схема выгоднее?
2.3 Рассматриваются два варианта покупки квартиры: заплатить сразу 250 тыс. руб. или платить ежемесячно по 800 руб. в течение 10 лет при ставке 8% годовых?
2.4 За какой срок сумма в 50 тыс. руб. достигнет 100 тыс. руб. при начислении процентов два раза в году по годовой процентной ставке16%?
2.5 Ссуда 60 тыс. долларов, выданная под 6% годовых погашается ежеквартальными платежами по 8 тыс. долларов. Рассчитайте срок погашения ссуды.
2.6 Пенсионер накопил в банке к моменту выхода на пенсию 30000 рублей. В конце каждого месяца ему начисляют пенсию в размере 2000 руб. Банк обеспечивает по пенсионному вкладу 14% годовых. Сколько лет пенсионер сможет снимать со своего вклада в конце каждого месяца по 3000 рублей?
2.7 Вы берете в банке ипотечную ссуду на покупку квартиры 350000 рублей. Первый взнос составляет 15% от стоимости квартиры. Годовая ставка банка 6%. Срок погашения 10 лет. Каковы должны быть ежемесячные взносы в банк, общая сумма, которую Вам придется заплатить, и Ваша переплата банку?
2.8 Пенсия начисляется пенсионеру в начале каждого месяца в размере 1300 рублей на его р/с в банке. Какая сумма накопится через 5 лет, если банк обеспечивает14,5% годовых? Какая сумма накопилась бы у пенсионера, если бы он копил пенсию в укромном уголке?
2.9 Сколько денег нужно положить в банк сегодня, чтобы при ежемесячных вложениях по 500 рублей и процентной ставке 12% в год через 5 лет накопить сумму 50000 рублей?
2.10 Ваша фирма собирается дать кредит в размере 1 000 000 рублей сроком на 5 лет с ежегодным погашением по 200 000 руб. Под какой процент следует дать кредит, чтобы в конце срока получить обратно в общей сложности 1 500 000 рублей?
2.11 Родители оставили Вам наследство 50 000 рублей. Вы решили через 3 года накопить на автомашину 100 000 рублей. Вы вложили деньги в банк под 12% годовых. Какую сумму Вам необходимо вносит ежемесячно? Сколько лет Вам бы пришлось копить эти деньги дома?
2.12 Вы решили накопить в банке 300 000 рублей на квартиру. Вначале Вы внесли 50 000 рублей и можете вкладывать в банк ежемесячно по 8000 рублей. Банк имеет годовую процентную ставку 11%. Сколько времени Вам придется копить эти деньги? Сколько времени Вы копили бы деньги дома?
2.13 Фирма собирается взять кредит в размере $100 000 сроком на 7 лет на приобретение сырья. Требуется выбрать наиболее выгодный (эффективный) банк по минимальной величине отношения выплачено/получено из трех банков, имеющих следующие характеристики.
| Банк | Выдача | Плата за оформление | Ставка (%) |
| Альфа | 0,96 | $350 | |
| Орион | 0,955 | $280 | 7,2 |
| Стройбанк | 0,95 | $350 |
Какова переплата банку по возвращении кредита?
2.14 Фирма взяла в банке кредит в размере $200 000 сроком на 7 лет под 7,2% годовых. Определить ежегодные выплаты и составить таблицу погашения основного долга, выплат по процентам и остатка долга по годам. Построить график.
2.15 Для обеспечения будущих расходов создается фонд, средства в который поступают в виде постоянной годовой ренты в течение 3 лет. Размер ренты 2 млн. руб. На поступившие взносы начисляются проценты по ставке 15% годовых. Определите наращенную сумму.
2.16 Для обеспечения будущих расходов создается фонд, средства в который поступают в виде постоянной годовой ренты в течение 5 лет. Размер разового платежа 1,5 млн. руб. На поступившие взносы начисляются проценты по ставке16% годовых. Определите полученную сумму, пересчитанную к началу платежей.
2.17 Создается страховой фонд фирмы общей суммой10 млн. руб. Фонд должен быть создан в течение3 лет. Ежегодные платежи пренумерандо. Проценты начисляются 2 раза в год. Определите размер платежа и текущую стоимость суммы.
2.18 Пенсионер собирает деньги на покупку телевизора стоимостью 7000 руб. Для этого он вкладывает в банк ежемесячно в конце месяца по 200 руб. Номинальная процентная ставка банка - 16%. Начисление процентов ежемесячное. Сколько времени ему придется копить деньги? Сколько времени пенсионеру пришлось бы копить деньги, складывая их в банку из-под кофе?
2.19 В конце каждого месяца семья вкладывает в банк по 5000 руб. под номинальную процентную ставку 20%. Начисление процентов ежемесячное. Какой срок необходим для того, чтобы сумма сбережения стала достаточной для покупки легкового автомобиля стоимостью 250 тыс. руб.?
2.20 Какую сумму фирма должна ежемесячно переводить в банк постнумерандо, чтобы на ее счете через 2 года накопилась сумма 3 млн. руб.? Номинальная процентная ставка банка - 12% при ежеквартальном начислении процентов.
2.21 Продается здание сметной стоимостью 2,6 млн. руб. Продавец предлагает оплату равными месячными платежами в течение 2 лет. Начисление процентов ежемесячное, годовая процентная ставка 18%. Покупатель предлагает следующие условия: оплата равными квартальными платежами в течение 3 лет. Начисление процентов 2 раза в год под номинальную процентную ставку 16% годовых. Определите величину годовых платежей и общую наращенную сумму для обоих вариантов.
2.22 Фирма реализует автомобиль стоимостью 350 тыс. руб. Возможны следующие варианты оплаты:
1) аванс - 15%. Остаток стоимости - в кредит сроком на год под номинальную процентную ставку 20% годовых. Начисление процентов ежемесячное. Равные платежи по кредиту производятся поквартально;
2) аванс - 20% стоимости. Возможна отсрочка платежей на 3 месяца. Кредит начисляется и выплачивается ежемесячно равными суммами в течение года. Годовая процентная ставка 22%;
3) аванс - 20% стоимости кредита. Кредит начисляется и выплачивается немедленно в течение 2 лет ежеквартально равными суммами. Годовая процентная ставка 24%; начисление процентов раз в полгода.
Рассчитайте финансовые последствия трех вариантов: аванс, разовые платежи, годовые платежи, общую сумму выплат.
2.23 Стоимость квартиры 250 000 руб. Начальный взнос составляет 25% от стоимости квартиры. Ипотечная ссуда выдана на 12 лет под процентную ставку 8%. Определите ежегодные выплаты по ссуде и сумму переплаты банку.
2.24 Продается складское помещение сметной стоимостью 350 тыс.. руб. Продавец предлагает оплату равными квартальными платежами в течение 1 года. Начисление процентов ежемесячное, годовая процентная ставка 15%. Покупатель предлагает следующие условия: оплата равными полугодовыми платежами в течение 2 лет. Начисление процентов 4 раза в год под номинальную процентную ставку 12% годовых. Определите величину годовых платежей и общую наращенную сумму для обоих вариантов.
2.25 Фирма реализует автомобиль стоимостью 500 тыс. руб. Возможны следующие варианты оплаты:
1) аванс - 25%. Остаток стоимости - в кредит сроком на 2 года под номинальную процентную ставку 15% годовых. Начисление процентов ежеквартальное. Равные платежи по кредиту производятся ежемесячно;
2) аванс - 20% стоимости. Возможна отсрочка платежей на 3 месяца. Кредит начисляется и выплачивается ежеквартально равными суммами в течение 3 лет. Годовая процентная ставка 12%.
Глава 3
ОБЩИЙ ПОТОК ПЛАТЕЖЕЙ

 С=
С=  Такую сумму фирме следует начислять ежемесячно в страховой фонд.
Такую сумму фирме следует начислять ежемесячно в страховой фонд.  (2.17) Назовем f(r) функцией цели.
(2.17) Назовем f(r) функцией цели. 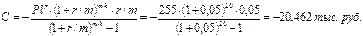 Эту же величину можно рассчитать с помощью функции ППЛАТ(0,05; 20; 255)= - 20,462 тыс. руб.
Эту же величину можно рассчитать с помощью функции ППЛАТ(0,05; 20; 255)= - 20,462 тыс. руб.