Ортогональная система двух и трех плоскостей проекций.

Лекция 1

1. Точка, прямая и плоскость.Ортогональная система двух и трех плоскостей проекций. Точка. Прямая линия. Взаимное положение прямых. Плоскость, прямые и точки, лежащие в плоскости. Взаимное положение двух плоскостей. Взаимное положение линии и плоскости. Первая позиционная задача. Виды метрических задач.

Ортогональная система двух и трех плоскостей проекций.

Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Г. Монжем.

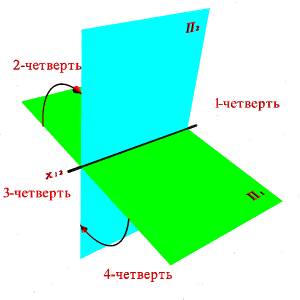
Рис. 1. Пространственная модель двух плоскостей проекций

Изложенный Монжем метод - метод ортогонального проецирования, причем берутся две проекции на две взаимно перпендикулярные плоскости проекций, - обеспечивая выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остается основным методом составления технических чертежей.

В соответствии с методом предложенным Г. Монжем рассмотрим в пространстве две взаимно перпендикулярные плоскости проекций (рис.1). Одну из плоскостей проекций П1 располагают горизонтально, а вторую П2 - вертикально. П1 - горизонтальная плоскость проекций, П2- фронтальная. Плоскости бесконечны и непрозрачны.

Плоскости проекций делят пространство на четыре двугранных угла – четверти. Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций.

Линия пересечения плоскостей проекций называется осью координат и обозначается х1,2.

Так как эти плоскости непрозрачны, то видимыми для наблюдателя будут только те геометрические объекты, которые располагаются в пределах той же первой четверти.

Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость П1 совмещают вращением вокруг оси x12 с плоскостью П2 (рис.1.6). Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещенные определенным образом одна с другой, называется эпюром (франц. Epure – чертеж.). Эпюр часто называют эпюром Монжа.

Геометрические объекты делятся на: линейные (точка, прямая, плоскость), нелинейные (кривая линия, поверхность) и составные (многогранники, одномерные и двумерные обводы).

ТОЧКА

Взаимное расположение точек

Можно выделить три основных варианта взаимного расположения точек:

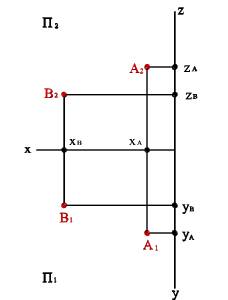
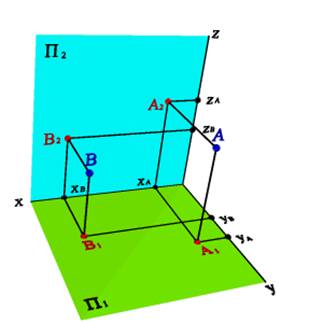
Рис. 4.Взаимное расположение точек

1.Пусть точки А и В (рис.4) расположены в первой четверти так, что:

- YА>YВ. Тогда точка А расположена дальше от плоскости П2 и ближе к наблюдателю, чем точка В

- ZА>ZВ. Тогда точка А расположена дальше от плоскости П1 и ближе к наблюдателю, чем точка В;

- XА<XВ. Тогда точка В расположена дальше от плоскости П3 и ближе к наблюдателю, чем (при взгляде слева) точка А;

2. – YА=YВ, то точки А и В равноудалены от плоскости П2 и их горизонтальные проекции расположатся на прямой А1В1//x12. Геометрическим местом таких точек служит плоскость, параллельная П2.

– ZА=ZВ, то точки А и В равноудалены от плоскости П1 и их фронтальные проекции расположатся на прямой А2В2//x12. Геометрическим местом таких точек служит плоскость, параллельная П1.

– XА=XВ, то точки А и В равноудалены от плоскости П3 и их горизонтальные и фронтальные проекции расположатся, соответственно, на прямых А1В1//y и А2В2//z . Геометрическим местом таких точек служит плоскость, параллельная П3.

3. Если у точек равны две одноименные координаты, то они называются конкурирующими. Конкурирующие точки расположены на одной проецирующей прямой. На рис. 5 даны три пары таких точек, у которых:

XА=XD;YА=YD;ZА>ZD; XA=XC;ZA=ZC;YA>YC; YA=YB;ZA=ZB;XA>XB;

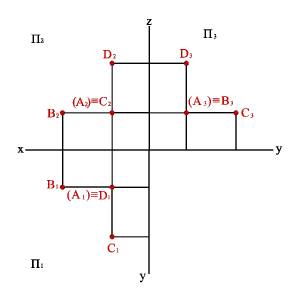
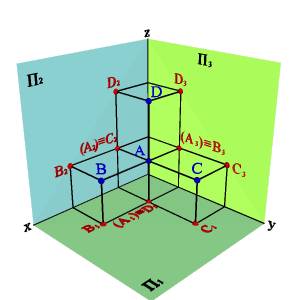
Рис. 5. Конкурирующие точки

Различают: горизонтально конкурирующие точки А и D, расположенные на горизонтально проецирующей прямой АD; фронтально конкурирующие точки A и C расположенные на фронтально проецирующей прямой AC; профильно конкурирующие точки A и B, расположенные на профильно проецирующей прямой AB.

При проецировании на соответствующую плоскость проекций одна точка «закроет» другую точку, конкурирующую с ней, соответствующая проекция которой окажется невидимой.

Прямая линия

Способы графического задания прямой линии

Для определения положения прямой в пространстве существуют следующие методы:

1.Двумя точками (А и В).

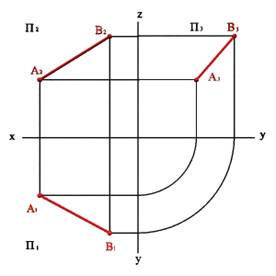
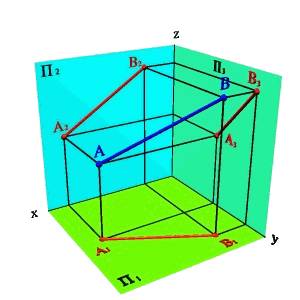
Рис. 6. Определение положения прямой по двум точкам

Рассмотрим две точки в пространстве А и В (рис.6). Через эти точки можно провести прямую линию получим отрезок [AB]. Для того чтобы найти проекции этого отрезка на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка: [A1B1]<[AB]; [A2B2]<[AB]; [A3B3]<[AB].

2. Двумя плоскостями (a; b).

Этот способ задания определяется тем, что две непараллельные плоскости пересекаются в пространстве по прямой линии.

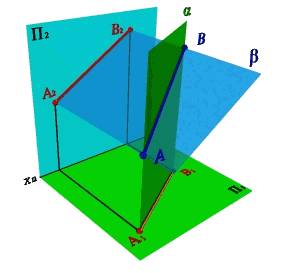
Рис. 7. Определение положения прямой в пространстве по двум проекциям отрезка

3. Двумя проекциями.

Пусть в плоскостях П1 и П2 даны проекции прямых заданных отрезками [А1В1] и [A2B2]. Проведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис.7), линией их пересечения будет прямая заданная отрезком [АВ], проекциями которой являются отрезки [А1В1] и [А2В2].

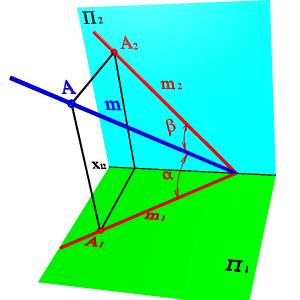
Рисунок 8. Определение положения прямой по точке и углам наклона к плоскостям проекций

4. Точкой и углами наклона к плоскостям проекций.

Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве (рис.8).

Следы прямой линии.

Следом прямой линии называется точка (рис.17), в которой прямая пересекается с плоскостью проекций (так как след принадлежит одной из плоскостей проекций то его одна координата должна быть равна нулю).

Горизонтальный след - М (zM=0)-точка пересечения прямой с горизонтальной плоскостью проекций.

Фронтальный след - N (yN=0)- точка пересечения прямой с фронтальной плоскостью проекций.

Профильный след - Т (xТ=0)- точка пересечения прямой с профильной плоскостью проекций.

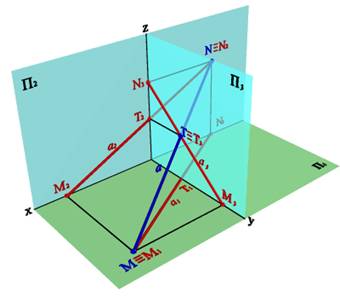
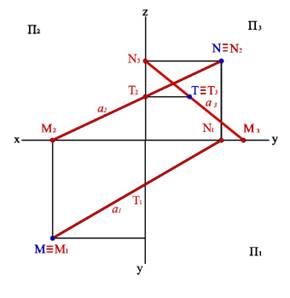
Рис. 17. Следы прямой линии в системе трех плоскостей проекций

Следы прямой являются точками частного положения. Одноименные проекции следа прямой совпадают с самим следом, а другие проекции лежат на осях. Например, фронтальный след прямой N2ºN, а N1 лежит на оси x, N3 - на оси z. Отмеченные особенности в расположении следов проекций позволяет сформулировать следующие правила:

1. Для построения горизонтального следа М прямой необходимо продолжить ее фронтальную проекцию до пересечения с осью 0x и в этой точке восстановить перпендикуляр к оси до пересечения с горизонтальной проекцией прямой.

2. Для построения фронтального следа N прямой нужно из точки пересечения горизонтальной проекции её с осью 0x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой.

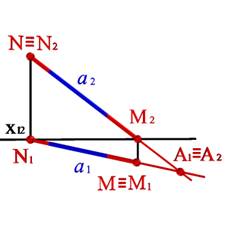
Рис. 18. Нахождение горизонтального и фронтального следов прямой линии

С помощью этих правил найдены на эпюре следы прямой а (рис.18) . Здесь же показаны совпавшие проекции точки А принадлежащей рассматриваемой прямой.

Следы прямой, являются точками, в которых прямая переходит из одного октанта в другой, позволяют отмечать её видимость. Видимой частью прямой будет та, которая расположена в пределах первого октанта.

Параллельные прямые линии.

Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.

Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны.

Это свойство параллельного проецирования остается справедливым и для ортогональных проекций, то есть если AB//CD то A1B1//C1D1; A2B2//C2D2; A3B3//C3D3 (рис.23). В общем случае справедливо и обратное утверждение.

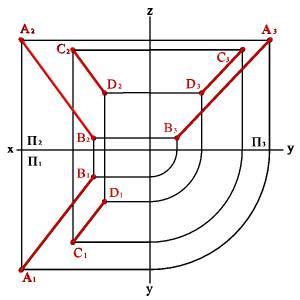
Рисунок 23. Параллельные прямые

Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых параллельны, но для оценки их взаимного положения необходимо сделать проекцию на профильную плоскость проекций (рис. 24). В рассмотренном случае проекции отрезков на плоскость П3 пересекаются, следовательно, они не параллельны.

Решение этого вопроса можно получить сравнением двух соотношений если:

А2В2/ А1В1= С2Д2/ С1 Д1Þ АВ//СД

А2В2/ А1В1¹ С2Д2/ С1Д1Þ АВ#СД

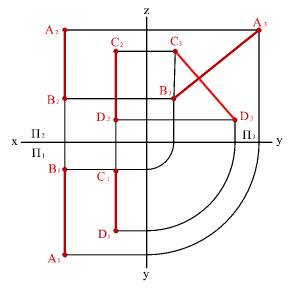
Рисунок 24. Прямые параллельные профильной плоскости проекций

2. Пересекающиеся прямые.

Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку.

Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи (рис. 25).

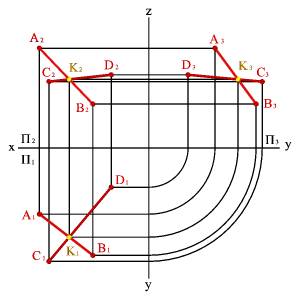
Рис. 25. Пересекающиеся прямые

В общем случае справедливо и обратное утверждение, но есть два частных случая:

1. Если одна из прямых параллельна какой-либо из плоскостей проекций, например профильной плоскости проекций (рис. 26), по двум проекциям невозможно судить об их взаимном расположении. Так горизонтальная и фронтальная проекции отрезков АВ и СД пересекаются, причем точка пересечения проекций лежит на одной линии связи, профильные проекции этих отрезков тоже пересекаются, однако точка их пересечения не лежит на одной линии связи с точками пересечения горизонтальной и фронтальной проекций отрезков, следовательно, не пересекаются и сами отрезки.

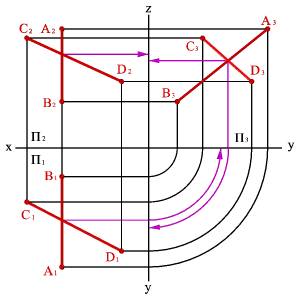
Рис. 26.Одна из прямых параллельна профильной плоскости проекций

2. Пересекающие прямые расположены в общей для них проекционной плоскости, например перпендикулярной фронтальной плоскости проекций (рис. 27). О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной проекции, например, на горизонтальную плоскость проекций (А1В1∩С1D1ÞАВ∩СD)

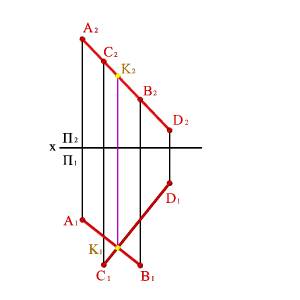
Рис. 27. Пересекающиеся прямые расположены в фронтально проецирующей плоскости

Скрещивающиеся прямые

Скрещивающимися называются две прямые не лежащие в одной плоскости.

Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи.

Точке пересечения фронтальных проекций прямых (рис. 28) соответствуют две точки А и В, из которых одна принадлежит прямой а, другая в . Их фронтальные проекции совпадают лишь потому, что в пространстве обе точки А и В находятся на общем перпендикуляре к фронтальной плоскости проекций. Горизонтальная проекция этого перпендикуляра, обозначенная стрелкой, позволяет установить, какая из двух точек ближе к наблюдателю. На предложенном примере ближе точка В лежащая на прямой в, следовательно, прямая в проходит в этом месте ближе прямой а и фронтальная проекция точки В закрывает проекцию точки А. (Для точек С и Д решение аналогично).

Этот способ определения видимости по конкурентным точкам. В данном случае точки А и В- фронтально конкурирующие, а С и Д -горизонтально конкурирующие.

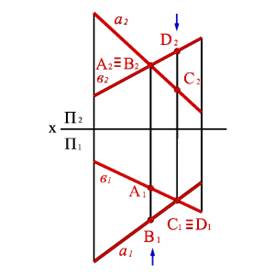
Рисунок 28. Скрещивающиеся прямые

Проекции плоских углов

Угол - геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Углом между прямыми называется меньший из двух углов между лучами, параллельными этим прямым. Углом между плоскостью и не перпендикулярной ей прямой называется угол между прямой и её проекцией на данную плоскость.

Рассмотрим ряд свойств ортогональных проекций плоских углов:

1. Если хотя бы одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость прямой угол проецируется без искажения (Теорема о проецировании прямого угла)

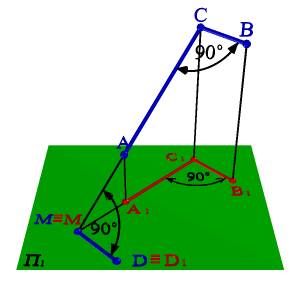
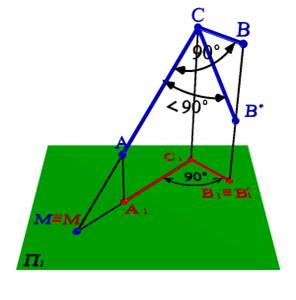
Рис. 29. Теорема о проецировании Рис. 30. Обратная теорема о проецировании

прямого угла прямого угла

Дано: ÐАВС = 90о; [ВС] // П1; [АС] # П1.

Для доказательства теоремы продлим отрезок АС до пересечения с плоскостью П1 (рис. 29) получим горизонтальный след прямой - точку М º М1, одновременно принадлежащую прямой и ее проекции. Из свойства ортогонального проецирования следует, что [ВС] // [В1С1]. Если через точку М проведем прямую МD параллельную С1В1, то она будет параллельна и СВ, а следовательно ÐСМD= 90°. Согласно теореме о трех перпендикулярах ÐС1МD=90° Таким образом, [MD]^[А1С1] и [MD]//[В1С1], следовательно, ÐА1С1В1= 90°, что и требовалось доказать. В случае когда [АС]^П1 проекцией угла, согласно свойствам ортогонального проецирования, будет прямая линия.

2. Если проекция угла представляет угол 90°, то проецируемый угол будет прямым лишь при условии, что одна из сторон этого угла параллельна плоскости проекций (рис. 30).

3. Если обе стороны любого угла параллельны плоскости проекций, то его проекция равна по величине проецируемому углу.

4. Если стороны угла параллельны плоскости проекций или одинаково наклонены к ней, то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве.

5. Если стороны угла не параллельны плоскости проекций, то угол на эту плоскость проецируется с искажением.

Лекция 2

2. Способы преобразования проекций. Характеристика способов. Способ замены плоскостей проекций. Способ вращение. Способ косоугольного вспомогательного проецирования.

Методы преобразования ортогональных проекций

Если прямая параллельна одной из плоскостей проекций т.е. является прямой уровня, то без преобразования ортогональных проекций можно только найти проекции перпендикуляра. Пусть прямая f фронталь, т.е. f \\ П2 значит перпендикуляр можно проводить из проекций А2 к фронтальной проекции прямой m2, на эту плоскость угол будет проецироваться без искажения (рис. 32). Однако полученные проекции отрезка АК не отражают истинной величины отрезка потому, что АК - отрезок прямой общего положения.

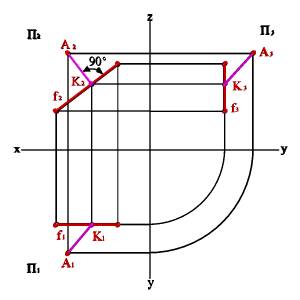
Рис. 32. Расстояние от точки до фронтальной прямой

Общий случай подобной задачи, когда требуется найти расстояние от точки до прямой общего положения, то даже построение проекции искомого отрезка без преобразования проекций не представляется возможным.

Сопоставление приведенных чертежей показывает, что трудности решения одной и той же задачи существенно зависят от положения геометрических объектов относительно плоскостей проекций.

В связи с этим, естественно, возникает вопрос, каким путем можно получить удобные проекции для решения поставленной задачи по заданным неудобным ортогональным проекциям.

Переход от общего положения геометрической фигуры к частному можно осуществлять за счет изменения взаимного положения проецируемой фигуры и плоскостей проекций.

При ортогональном проецировании это достигается двумя путями:

1. Перемещение в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве - метод плоскопараллельного перемещения.

2. Перемещением плоскостей проекций в новое положение по отношению, к которому проецируемая фигура (которая не меняет положения в пространстве) окажется в частном положении - метод замены плоскостей проекций.

Плоскости проекций

Плоскости носитель траекторий перемещения точек параллельны плоскости проекций. Траектория - дуга окружности, центр которой находится на оси перпендикулярной плоскости проекций. Для определения натуральной величины отрезка прямой общего положения АВ (рис. 34), выберем ось вращения перпендикулярную горизонтальной плоскости проекций и проходящую через В1. Повернем отрезок так, чтобы он стал параллелен фронтальной плоскости проекций (горизонтальная проекция отрезка параллельна оси x). При этом точка А1 переместиться в А*1, а точка В не изменит своего положения. Положение точки А*2 находится на пересечении фронтальной проекции траектории перемещения точки А (прямая линия параллельная оси x) и линии связи проведенной из А*1. Полученная проекция В2 А*2 определяет действительные размеры самого отрезка.

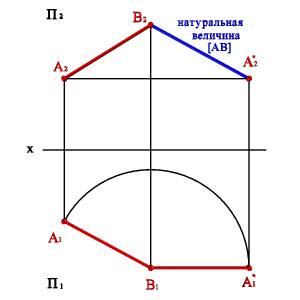
Рис. 34. Определение натуральной величины отрезка методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций

Плоскости проекций

Рассмотрим этот способ на примере определения угла между пересекающимися прямыми (рис.35). Рассмотрим две проекции пересекающихся прямых а и в которые пересекаются в точке К. Для то чтобы определить натуральную величину угла между этими прямыми необходимо произвести преобразование ортогональных проекций так, чтобы прямые стали параллельны плоскости проекций. Воспользуемся способом вращения вокруг линии уровня - горизонтали. Проведем произвольно фронтальную проекцию горизонтали h2 параллельно оси Ох, которая пересекает прямые в точках А2 и В2 . Определив проекции А1 и В1, построим горизонтальную проекцию горизонтали h1 . Траектория движения всех точек при вращении вокруг горизонтали - окружность, которая проецируется на плоскость П1 в виде прямой линии перпендикулярной горизонтальной проекции горизонтали.

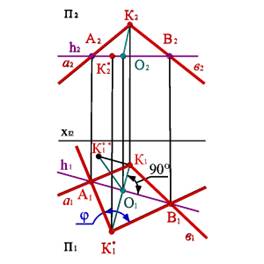
Рис. 35. Определение угла между пересекающимися прямыми, вращением вокруг оси параллельной горизонтальной плоскости проекций

Таким образом, траектория движения точки К1 определена прямой К1О1, точка О -центр окружности - траектории движения точки К. Чтобы найти радиус этой окружности найдем методом треугольника натуральную величину отрезка КО .Продолжим прямую К1О1 так чтобы |КО|=|О1К*1| . Точка К*1 соответствует точке К , когда прямые а и в лежат в плоскости параллельной П1 и проведенной через горизонталь - ось вращения. С учетом этого через точку К*1 и точки А1 и В1 проведем прямые, которые лежат теперь в плоскости параллельной П1, а следовательно и угол j - натуральная величина угла между прямыми а и в.

Плоскость

Плоскость – одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости:

1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки;

2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.

Способы графического задания плоскостей

Положение плоскости в пространстве можно определить:

1. Тремя точками, не лежащими на одной прямой линии (рис.38);

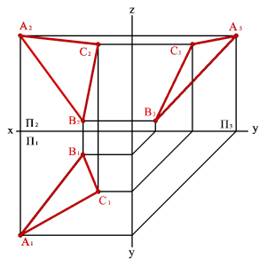Рис. 38. Плоскость заданная тремя точками, не лежащими на одной прямой

2. Прямой линией и точкой, не принадлежащей этой прямой (рис.39);

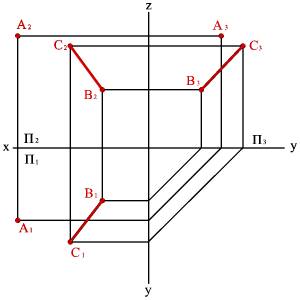
Рис. 39. Плоскость заданная прямой линией и точкой, не принадлежащей этой линии

3. Двумя пересекающимися прямыми (рис.40);

Рисунок 40. Плоскость заданная двумя пересекающимися прямыми линиями

4. Двумя параллельными прямыми (рис.41)

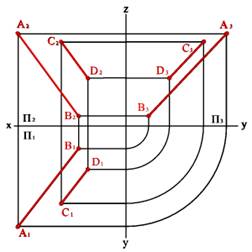Рис. 41. Плоскость заданная двумя параллельными прямыми линиями

5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис.42)..

Следом плоскости называется прямая линия по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная a плоскость различают горизонтальный aП1, фронтальный aП2 и профильный aП3 следы.

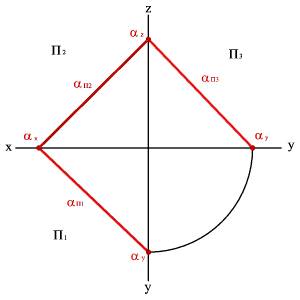
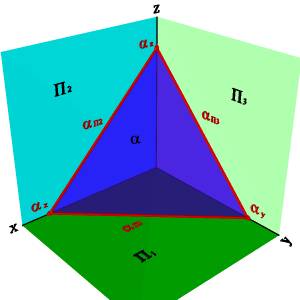
Рисунок 42. Плоскость заданная следами

Плоскостей проекций

В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный aП1; - фронтальный aП2; - профильный aП3).

Следы плоскости общего положения пересекаются попарно на осях в точках ax,ay,az. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.

Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях (рис.42).

2.Плоскости перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:

2.1. Плоскость перпендикулярная горизонтальной плоскости проекций (a^P1), называется горизонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек любых фигур в этой плоскости совпадают с горизонтальным следом (рис.43).

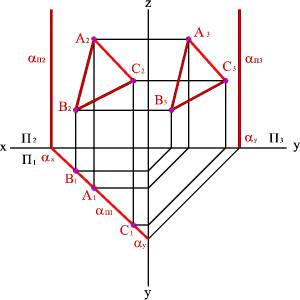
Рис. 43. Горизонтально проецирующая плоскость

2.2. Плоскость перпендикулярная фронтальной плоскости проекций (a^П2)- фронтально проецирующая плоскость. Фронтальной проекцией плоскости a является прямая линия, совпадающая со следом aП2 (рис.44).

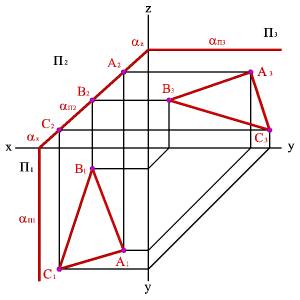
Рисунок 44. Фронтально проецирующая плоскость

2.3. Плоскость перпендикулярная профильной плоскости (a^П3) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рис.45).

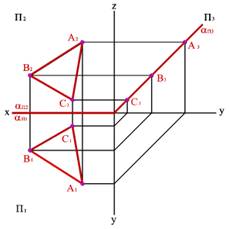Рисунок 45. Биссекторная плоскость

3. Плоскости параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельны исследуемая плоскость, различают:

3.1. Горизонтальная плоскость - плоскость параллельная горизонтальной плоскости проекций (a//П1) - (a^П2,a^П3). Любая фигура в этой плоскости проецируется на плоскость П1 без искажения, а на плоскости П2 и П3 в прямые - следы плоскости aП2 и aП3 (рис.46).

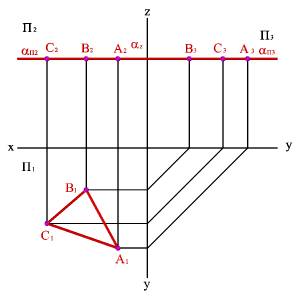
Рисунок 46. Горизонтальная плоскость

3.2. Фронтальная плоскость - плоскость параллельная фронтальной плоскости проекций (a//П2), (a^П1, a^П3). Любая фигура в этой плоскости проецируется на плоскость П2 без искажения, а на плоскости П1 и П3 в прямые - следы плоскости aП1 и aП3 (рис.47).

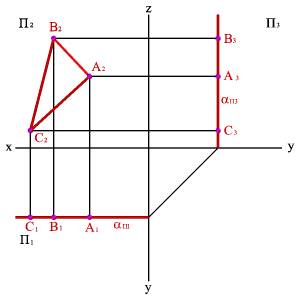
Рисунок 47. Фронтальная плоскость

3.3. Профильная плоскость - плоскость параллельная профильной плоскости проекций (a//П3), (a^П1, a^П2). Любая фигура в этой плоскости проецируется на плоскость П3 без искажения, а на плоскости П1 и П2 в прямые - следы плоскости aП1 и aП2 (рис.48).

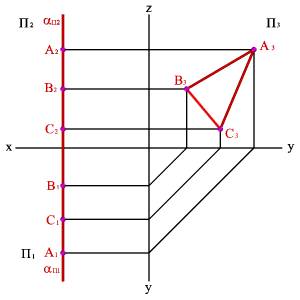
Рисунок 48. Профильная плоскость

Следы плоскости

Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают: горизонтальный, фронтальный и профильный следы плоскости.

Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой ( как для построения любой прямой). На рис. 49 показано нахождение следов плоскости α(АВС). Фронтальный след плоскости αП2, построен, как прямая соединяющая две точки N(АС) и N(АВ), являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости α. Горизонтальный след αП1 – прямая, проходящая через горизонтальные следы прямых ВС и АВ. Профильный след αП3 – прямая соединяющая точки (αy и αz) пересечения горизонтального и фронтального следов с осями.

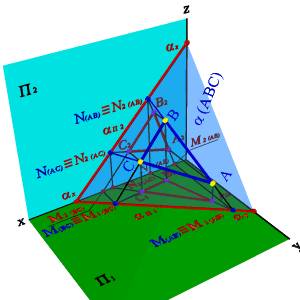
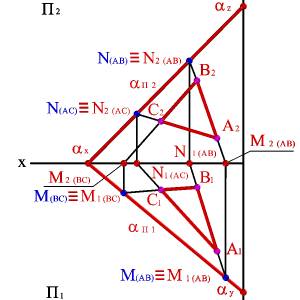
Рис. 49. Построение следов плоскости

Главные линии в плоскости

Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:

1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (hÎАВС, h//P1, h2//Ох,h3//Оy)(рис.53).

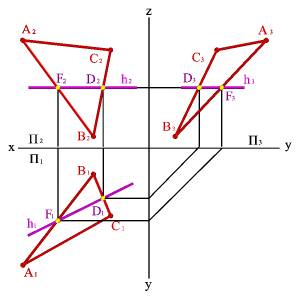
Рис 53. Горизонталь

2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (fÎАВС, f//P2, f1//Ох, f3//Оz)(рис.54).

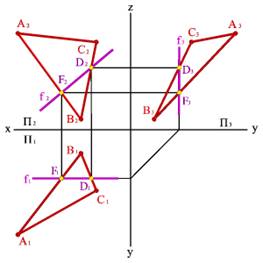
Рис. 54. Фронталь

3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (рÎАВС, р//P3, р1^Ох, р2^Ох) (рис.55).

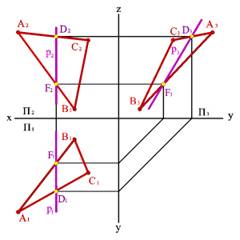
Рисунок 55. Профильная прямая

Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.

4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.56).

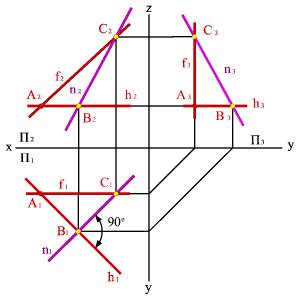
Рис. 56. Линия наибольшего ската

Лекция 1

1. Точка, прямая и плоскость.Ортогональная система двух и трех плоскостей проекций. Точка. Прямая линия. Взаимное положение прямых. Плоскость, прямые и точки, лежащие в плоскости. Взаимное положение двух плоскостей. Взаимное положение линии и плоскости. Первая позиционная задача. Виды метрических задач.

Ортогональная система двух и трех плоскостей проекций.

Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Г. Монжем.

Рис. 1. Пространственная модель двух плоскостей проекций

Изложенный Монжем метод - метод ортогонального проецирования, причем берутся две проекции на две взаимно перпендикулярные плоскости проекций, - обеспечивая выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остается основным методом составления технических чертежей.

В соответствии с методом предложенным Г. Монжем рассмотрим в пространстве две взаимно перпендикулярные плоскости проекций (рис.1). Одну из плоскостей проекций П1 располагают горизонтально, а вторую П2 - вертикально. П1 - горизонтальная плоскость проекций, П2- фронтальная. Плоскости бесконечны и непрозрачны.

Плоскости проекций делят пространство на четыре двугранных угла – четверти. Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций.

Линия пересечения плоскостей проекций называется осью координат и обозначается х1,2.

Так как эти плоскости непрозрачны, то видимыми для наблюдателя будут только те геометрические объекты, которые располагаются в пределах той же первой четверти.

Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость П1 совмещают вращением вокруг оси x12 с плоскостью П2 (рис.1.6). Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещенные определенным образом одна с другой, называется эпюром (франц. Epure – чертеж.). Эпюр часто называют эпюром Монжа.

Геометрические объекты делятся на: линейные (точка, прямая, плоскость), нелинейные (кривая линия, поверхность) и составные (многогранники, одномерные и двумерные обводы).