Простые проценты и их применение в финансово-экономических расчетах.

Все большую актуальность получают вопросы расчета и про­гнозирования финансово-экономических показателей. В совре­менных условиях финансовые математические модели представ­ляют собой неотъемлемую и очень важную часть статистического анализа с целью выработки и принятия решений.

В финансово-экономических расчетах денежные потоки (сумма денег) всегда связываются с конкретными интервалами времени. В связи с этим в финансовых сделках (договорах, контрактах) обязательно даются фиксированные сроки, даты, периодичность выплат (или поступление денежных средств). В финансовой ма­тематике фактор времени учитывается с помощью исчисления (применения) процентной ставки, учитывающей интенсивность начисления процентов (процентных денег). Процентная ставка — это отношение суммы процентных денег, выплачиваемых за строго зафиксированный отрезок времени, к величине кредита, ссуды и т.д. Интервал времени, к которому приурочена процентная став­ка, называется периодом начисления (накопления).

Ставки процентов могут применяться к одной и той же на­чальной сумме на протяжении всего срока действия кредита, ссуды. Такого рода проценты называются простыми процентны­ми ставками. В этом случае распределение суммы накопления описывается равномерным линейным законом распределения, а сам процесс наращения может быть выражен в виде арифме­тической профессии:

FV=PV(1 +n * i) или FV=PV + I,

где FV — наращенная сумма;

PV — текущая (первоначальная) сумма;

n — количество периодов начислений;

i — ставка процентов;

i= PV * п * i — процентный доход за весь срок.

В некоторых случаях возможно применение дискретно изме­няющихся во времени процентных ставок. Например, ставка про­стого процента в первый год равна 10%, во второй — 15%, в третий — 20%.

Когда периоды начисления (например, по годам) равны, то формула наращения по простым процентам имеет вид: FV=PV (1+n-i)^m,

где m — общее число операций реинвестирования.

В отечественной практике, как правило, не делают различий между понятиями ссудного (кредитного) процента и учетной ставки. Обычно применяют собирательный термин — процент­ная ставка. В то же время термин учетная ставка встречается применительно к ставке рефинансирования ЦБ РФ, а также к вексельным операциям.

Нужно подчеркнуть, что начисление процентов в большин­стве случаев осуществляется в конце каждого периода (интерва­ла) начисления. Такой способ определения и начисления про­центов носит название декурсивного способа. В отдельных случа­ях в соответствии с заключенными договорами применяется антисипативный (предварительный) способ, т.е. проценты на­числяются в начале каждого периода начисления.

В финансовых расчетах наиболее часто встречаются задачи по определению наращенной суммы FV по заданной (первона­чальной) величине текущей стоимости ссуды (кредита) PV, а также текущей суммы (полученной) PV по заданной наращен­ной сумме FV. Первый тип задач называется компаудингом (про­цессом накопления), второй тип задач — дисконтированием. Раз­ница величин текущей стоимости PV наращенной суммы FV называется дисконтом D_k, т.е.D_K = FV – PV.

Простые проценты могут быть точными, когда при расчете год берется равным фактической его продолжительности в днях, или обыкновенными, когда длительность года берется равной 360 дням. Принятое количество дней в году называется временной базой.

Cуществуют и такие понятия, как ком­мерческий (или банковский) учет, учет векселей, дисконтирова­ние по учетной ставке (по простым процентам). В практике фи­нансово-кредитных отношений простые учетные ставки приме­няются при учете векселей и других денежных обязательств. В зависимости от формы представления капитала и способа выпла­ты дохода ценные бумаги подразделяются на две группы: долговые (купонные облигации, сертификаты, векселя — имеющие фикси­рованную процентную ставку) и долевые (акции), представляю­щие долю держателя в реальной собственности и обеспечивающие получение дивиденда в неограниченное время. Все прочие виды ценных бумаг являются производными от долговых и долевых: это опционы, фьючерсные контракты, приватизационные чеки.

С целью избежания ошибок и потерь в условиях инфляции (снижения покупательной способности денег) нужно учитывать механизм влияния инфляции на результат финансовых опера­ций. При расчетах используют относительную величину уровня инфляции, т.е. темп инфляции α: α=(PV_α – PV)/PV или α= РV/PV*100

где α — темп инфляции;

PV_α — сумма, отражающая фактическую покупательную спо­собность (фактическую стоимость товара через пери­од времени /);

PV — сумма при отсутствии инфляции;

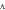РV= PV_α – PV – сумма инфляционных денег.

Cущность простых процентов заклю­чается в том, что они начисляются на одну и ту же величину капитала в течение всего срока ссуды (кредита).

В практике проведения финансовых расчетов дата выдачи и дата погашения ссуды всегда считаются за один день. При этом используют один из двух вариантов

1)точный процент получают, когда за временную базу берут фактическое число дней в году (365 или 366) и точное число дней ссуды:

где Nд— продолжительность начисления в годах;

Д — продолжительность периода начисления в днях;

К — продолжительность года в днях.

Точное число дней ссуды Д определяется по специальной таблице, где показаны порядковые номера каждого дня года (из номера, соответствующего дню окончания займа (ссуды), вычи­тают номер первого дня);

2)обыкновенный процент получают, когда применяется при­близительное число дней ссуды, а продолжительность полного месяца принимается равной 30 дням. Этот метод применяется при погашении облигаций (займа). Наращенная сумма FVв этих случаях определяется из выражения

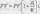
Определим ставку процентов, учитывающую инфляцию Iα, по формуле И. Фишера: