Полиномиальные производящие функции

1. Произведение (1+a₁x)(1+a₂x)·¼ ·(1+a_nx) порождает r-сочетания элементов {a₁,a₂,…,a_n} без повторений ( ):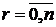

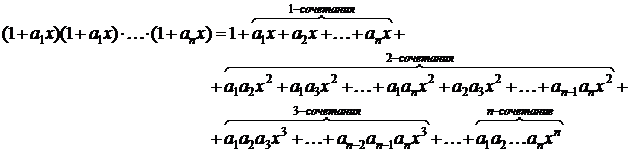
Коэффициенты при x^r ( 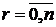) представляют собой все возможные r-сочетания из n разных предметов без повторений.

2. Если элемент a_i может входить в сочетания 0, 1, … , k раз (сочетания с повторениями, где количество a_i ограничено числом k), то в качестве сомножителя нужно взять .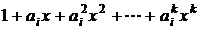

Например, пусть нужно получить все возможные сочетания, которые можно составить из множества, состоящего из 3 апельсинов, 2 мандаринов и 1 яблока. Поставим в соответствие апельсинам переменную a, мандаринам – м, яблокам – я и запишем произведение:

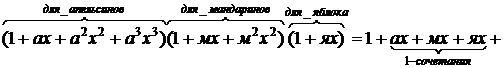
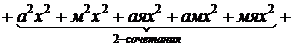
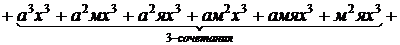
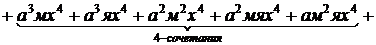
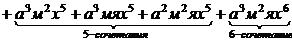
Коэффициенты при степенях x соответствуют различным сочетаниям. Например, коэффициент а³м²я соответствует сочетанию трех апельсинов, двух мандаринов и одного яблока (сочетание с повторениями аааммя).

Если после раскрытия скобок положить a₁= a₂₌…=a_n=1 и привести подобные, то коэффициент при x^r будет равен числу r-сочетаний. Например, в предыдущем примере положим а=м=я=1. Получим: (1+x+x²+x³)(1+x+x²)(1+x)=1+3x+5x²+6x³+5x⁴+3x⁵+x⁶.

Это означает, что из набора, содержащего 3 предмета первого типа, 2 предмета второго типа и 1 предмета третьего типа можно составить столько различных сочетаний (с повторениями):

0-сочетаний - 1

1-сочетаний - 3 (а, м, я)

2-сочетаний - 5 (аа, мм, ая, ам, мя)

3-сочетаний - 6 (ааа, аам, аая, амм, амя, ммя)

4-сочетаний - 5 (ааам, ааая, аамм, аамя, аммя)

5-сочетаний - 3 (ааамм, ааамя, ааммя)

6-сочетаний - 1 (аааммя)

Определение. Функция вида 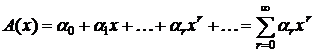называется полиномиальной производящей функцией. Полиномиальные производящие функции позволяют вычислять числа сочетаний различных типов.

В частности, бином Ньютона (1+x)ⁿ – производящая функция для r-сочетаний без повторений из n-множества. 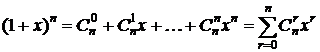. Коэффициент при x^r равен числу r-сочетаний без повторений .

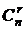А полином (1+x+x²+x³)(1+x+x²)(1+x) – производящая функция для r-сочетаний из множества, содержащего три предмета первого типа, два предмета второго типа и один предмет третьего типа.

В производящих функциях переменная х никак не определена и считается абстрактным символом. Она нужна только для того, чтобы по ее степени определить, какой r‑выборке соответствует стоящий при х^r коэффициент.

3. Пусть нужно найти число r-сочетаний из n типов элементов с неограниченными повторениями. По правилу составления полиномиальных функций, нужно записать произведение n скобок (так как у нас n типов элементов), в каждой из которой находится бесконечная сумма всех степеней x (так как число элементов каждого типа неограничено):

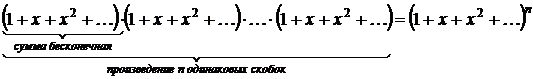
В скобках находится сумма бесконечной геометрической прогрессии:

.

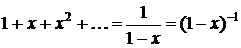Таким образом, производящая функция для числа сочетаний с неограниченными повторениями равна (1-х)^-n.

Разложим эту функцию в ряд по степеням x. Формально рассматривая эту (1-х)^-n как бином Ньютона с отрицательным показателем, получаем

.

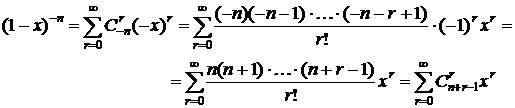Таким образом, разложив эту производящую функцию по степеням х, мы получаем числа r-сочетаний с повторениями - 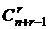, что совпадает с доказанным ранее: .

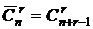Итак, (1+x)ⁿ – полиномиальная производящая функция для чисел r-сочетаний без повторений из n-множества ( );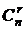

(1-x)^-n – полиномиальная производящая функция для r-сочетаний с неограниченными повторениями из n-множества ( ).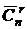

4. Если элементы n различных типов должны входить в сочетания только в четном количестве, то производящая функция будет следующей:

.

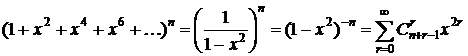Но для получения чисел сочетаний нужно, чтобы в полученной сумме степень x задавалась одной буквой, а не выражением. Поэтому положим 2r=k. Тогда r=k/2, и мы получаем ряд:

.

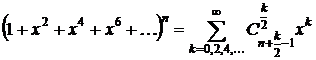Полученный ряд означает, что при нечетном k сочетаний не существует (нет слагаемых, в которых присутствует x в нечетной степени), а при четном k количество k-сочетаний с повторениями, где каждый предмет может входить только чётное число раз, равно 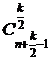при чётном k.

5. Если элементы n различных типов должны входить в сочетания только в количестве, кратном трем, то производящая функция будет следующей:

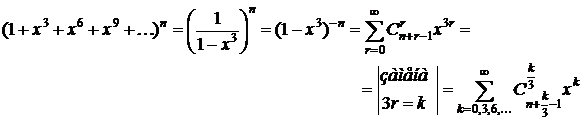
Следовательно, при k, не делящемся нацело на 3, сочетаний не существует (нет слагаемых, в которых присутствует x в степени, кратной 3), а при k, делящемся на 3, количество k-сочетаний с повторениями, где каждый предмет может входить только в количестве, кратном трем, равно .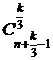

6. Пусть нужно определить числа сочетаний с повторениями, в которых предметы n различных типов входят хотя бы по одному разу (то есть предмет каждого типа обязательно должен присутствовать в сочетании). В этом случае при составлении производящей функции в каждой из скобок нужно исключить 1 (то есть степень x⁰):

.

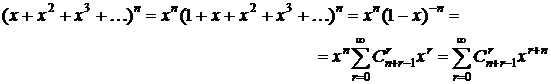Как и в предыдущих примерах, делаем замену переменных, чтобы степени x задавались одной буквой, а не выражением. Положим r+n=k, откуда r=k-n, и

.

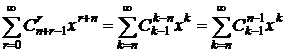(последнее равенство выполняется в силу симметричности биномиальных коэффициентов: 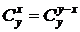). Из полученного ряда следует, что сочетаний меньше чем по n предметов не существует (нет слагаемых с x в степени, меньшей n). А при k≥n число k-сочетаний, в которые предметы каждого типа входят хотя бы по одному разу, равно .

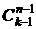Например, если есть предметы трех сортов: a, b, c (n=3), то сочетаний, в которые каждый из сортов входит хотя бы один раз, при k<3 нет, а при k≥3:

3-сочетаний: 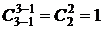- abc;

4-сочетаний: 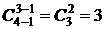- aabc, abbc, abcc;

5-сочетаний: 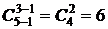- aaabc, aabbc, aabcc, abbbc, abbcc, abccc; и т.д.

Правила построения полиномиальных производящих функций:

1. Каждому сорту предметов соответствует одна скобка.

2. Каждой скобке сумма x^r.

3. Если предмет данного сорта может не входить в сочетание, то в скобке присутствует единица.

4. Ели предмет данного сорта может входить в сочетание только один раз, то в скобке присутствует х, если дважды – х², если трижды – х³, и т.д.

5. Если допускаются неограниченные повторения, то сумма в скобке бесконечна.

Правила использования полиномиальных производящих функций:

1. Производящую функцию разложить в ряд по степеням х.

2. Пользуясь заменой переменных, привести ряд к виду 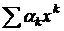(чтобы х был в степени одной буквы). В этом случае коэффициент при x^k даёт формулу для числа k-сочетаний при заданных условиях.

3. Подставив в эту формулу (в a_k) конкретные значения k и n, получим ответ на конкретный вопрос о числе k-сочетаний.