Формирование цен на облигации (О.).

О. предст-ет собой ц/б-гу, выпускаемую фирмами / гос-ом как ср-во заимствов-я долгоср. кредитов. Разл-ют срочн и бессрочн о. (имеющ. неогранич. прод-ть существ-я, консоли). Цена бесср. о. (В_{t бес.})- приведен. ст-ть будущ. %ых платежей: В_{t бес.}= 1/(1+i) + 1/(1+i)² +1/(1+i)³ +…Эта ∑- геометрич. прогресс. и м.б. выражена: В_{t бес.}=1/i или В_{t бес.}=d/i,где i-% ст., d- купон. д-д (долгоср. о. более чувствит. к Δям ст.%, чем краткоср.)

Кроме бессрочн. о. сущ-ют о., выпущенные на опред. срок, по истеч. ктр они погашаются. В данном случ. цена о. зависит от велич. выплат владельцу о. за период - купонн д-д (z); предстоящий срок ее обращ-я (T); ∑гашения в к. срока обращ-я (B); рын. ст. %(i). Согласно концепции капитализации д-дов: 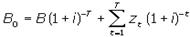(1)

где B₀ - цена о. в текущ (нулевом) пер. Обычно за все годы обращ-я о. див-ды выпл-ся в одинаковом размере: z₁ = z₂ = ... = z_T = a; тогда формула принимает вид:

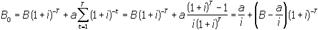(2)

Когда рын. курс о. < знач-я, получаемого по (2), тогда следует ожидать ↑курса, в противн. случ -↓. Кроме текущ. цены о. м. представлять интерес ее цена на мом-т погаш (B_T): 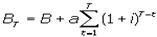(3). Она показывает, какую ∑денег получит владелец о. в мом-т ее погаш. в случ реинвестир-я всех дивид-ов под сложные %ы. Из 4 параметров (a, B, i, T), определяющих цену купонной о., a, B явл-ся известными константами. Рассмотрим, как влияют на цену о. Δ T и i . При a/B = i цена о. = ее номиналу независ от оставш-ся срока ее обращ-я, т.к. в этом случ выражение (2) принимает след вид: 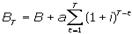t = 1,2, ... , T. Если a/B > i, то B_t > B, но по мере приближ-я к мом-ту гашения о. разность (B_t - B) ↓ся. Когда a/B < i, тогда B_t < B и B_t приближается к B снизу.

Проанализируем, как влияет на ценность о. Δi. Из выражения (1) следует, что при ее изменении с i₀ до i₁ нынешняя ценность о. Δся на: 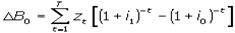(4)

где z_t при (t = T) - купонная выплата +∑ гашения о.

Из (4) следует, что ΔB₀ < 0 при i₁ > i₀, и наоборот, т.е. при ↑(↓) i цена о. ↓(↑). Соотв-но из (3) 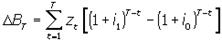(5)

Согласно (5) ΔB_T > 0 при i₁ > i₀, и наоборот, т.е. при ↑(↓) i владелец о. в мом-т ее гашения получит > (<), чем ожидал. Т.о., в случае ↑i нынешняя цена о. ↓, но к мом-ту ее гашения держатель о. при реинвест-ии див-ов б. иметь >, чем ожидал. При ↓i обладатель о. в тек периоде окажется богаче, но к мом-ту ее гашения он накопит меньшую ∑, чем при исходной i. Как Δся цена о. в каждом из периодов срока ее обращ-я при разлчных i:

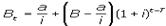
Пересечение кривых, представляющих динамику текущей цены о. в теч срока ее обращ-я при различных i, свид-ет о том, что сущ-ет опред. мом-т, в ктр текущая цена о. не зависит от Δi. В приведенном примере таким мом-ом является 4ый г. Эту особенность динамики ценности о. (капитализируемого д-да) в теории финн-ов используют при выработке рекомендаций по нейтрализации риска от изменения рын. i.
14. Мех-зм устан-я совместн равновесия на р-ках благ и фин Aвов при фиксир ценах.

Мод. IS-LM ,/ впервые предлож. Хиксом, позже развита Хансеном.

Совместн равновес - ситуац, при ктр реальн р-ды эк. субъектов=плановым, спрос на реальн ден ср-ва = предлож-ю денег, на р-ке благ и фин Авов одновр-но сущ-ет равновес.

Равнов на р. благ достигается при усл-ии, когда Iии=S, при этом величина Iий нах-ся в обратн завис-ти от велич i.Эта за­вис-ть отраж нисходящ хар-р кривой Iий. Т.к. Iии - часть совок р-дов, то при ↑ Iий, вызванном ↓ем i, отмечается и ↑р-дов, причем с мультиплик-ым эфф-ом→м/у Δ д-да и Δ i также сущ-ет связь, отраж-маякривой IS, кажд (.) ктр харак-ет ситуацию, когда плановые р-ды = объему нац. пр-ва.

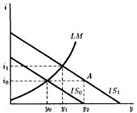Равновес на ден. р. возникает при =ве спроса и предлож. на деньги. Согласно кейнсианск. теор. предлож. денег - величина экзогенная, и равновесие б. зависеть от спроса на деньги, ктр в свою очередь опр-ся предпочт-­ем ликвидности, т. е. чем выше i, тем ниже спрос на деньги, т.к. i предст-ет альтернативные из­держки владения личными деньгами. Сокращ. ден. массы предопределяет ↑ i и ↓спроса на день­ги и, наоборот. В свою очередь, ↑спроса на деньги возрастает при ↑д-да. При этом, чт. сохранилось равнов., i тоже ↑. →сущ-ет завис-ть м/у ростом ур-ня д-да и i, что отражаеткривая LМ. Кривая LМ — мн-во гипотетических вводимых равновесных состояний на р. денег и ц/б.

Сам проц. приспособл-я ксовместн. равновесию зависит от того, какая конкр ситуация неравновесия сложилась на денеж­ном и товарном рынках.

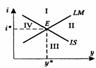
В модели с fix ценами кривые IS, LМ рассекают экон. пр-во на 4 области, каждая из ктр характ-т свое сост-е ден и товарн рынков: I-Избыток на р. благ и денег. II-Избыток тов-ов, дефицит денег. III-Деф-т благ и денег. IV-Деф-т тов-ов и избыток денег. Экон. равновесие IS-LМ — это (.) пересечения кри­вых, ктр опред-т равновесную %-ю ставку и эффектив­н спрос.

Эффективн. спрос — такой ур-нь запланир-ых р-дов, при ктр обесп-ся совместн равновес на р. благ и финн. Авов.

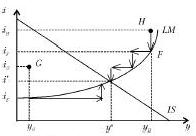
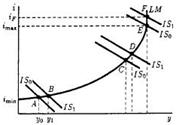
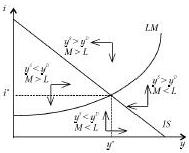Допустим, экон. конъюнктура находится в точке H.

При Y_H и i_H на р-ах благ и денег сущ-ет избыток предл-я (y_s>y_d и M>L). Поскольку планы участников сделок не совпадают др с др, последует корректировка D и S на обоих р. В больш-ве случ на ден. р. равновесие установится быстрее, т.к. д/Δя кол-ва находящихся в обращ денег треб-ся <t, чем для Δя объёма пр-ва. Тогда переход из H в * происх так: избыток S на ден. р. => ↓ие I => S денег ↓ся, а D ↑. При i_F и Y_H на ден. р.установится равновесие. На р. благ избыток (F выше IS). При fix ценах этот избыток ↓ся по 2 прич.: 1) ↓ие i увеличит Iый спрос предпр-лей 2) обнаружив сверхнормативн запасы гот. прод-ии, предпр-ли начнут сокращать пр-во=> нац. доход снизится. При i_F и Y<Y_H на ден р. вновь избыток и i ↓ся ещё больше. И т.д. Аналогично для точки G. избыток на рынке денег => ↓i и равновесие на ден. рынке. Из-за ↓i увеличится спрос на Iые блага и деф-т на р. благ. Поскольку предп-ся, что S благ при заданном ур-не цен совершенно эластично, деф-т устраняется за счет расшир-я пр-ва=> ↑д-да. При i_E и Y>Y_G деф-т на р. денег=>↑i. И т.д. Т.о. совместн равновесие на р. благ и денежном р. является устойчивым.

Для алгебраического опред-я параметров равновесия решается система из 2 уравнений вида IS: i=a-b*Y; LM: Y=c+i*d.