Дерево решений и максимизация полезности

Как уже отмечалось, согласно гипотезе, предложенной Бернулли и развитой Джоном фон Нейманом и Оскаром Моргенштерном, индивидов интересует ожидаемая полезность рисковых проектов. Функция полезности фон Неймана—Моргенштерна может отражать ранжирование любого количества обусловленных благ.

Выражение означает, что индивида фактически интересуют лишь количества обусловленных благ, но оценки этих благ потребителем зависят от вероятностей наступления исходов случайного процесса, ассоциируемых с возможностью их потребления. Вообще говоря, эти вероятности могут входить в функцию полезности достаточно сложным образом, однако имеется, как мы уже знаем, простой и практически важный способ их учета — частный случай, при котором относительное значение, придаваемое индивидом данному обусловленному благу, в точности пропорционально вероятности наступления ассоциируемого с его потреблением исхода. Это — функция ожидаемой полезности.

Расчеты ожидаемой полезности каждой из специализаций для Николая Александровича таковы.

В области финансового менеджмента:

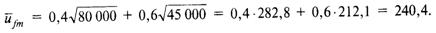
В области общего менеджмента:

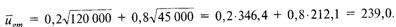
Выбирая вариант, сулящий наибольшую ожидаемую полезность, Николай Александрович решит специализироваться в области финансового менеджмента.

Сравнительная статика инвестиционного поведения.

Чтобы выявить степень несклонности к риску используют следующие коэффициенты:

Коэффициентом абсолютной несклонности к риску Эрроу-Пратта, r^A (x) называется r^A (x) = .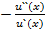

Коэффициентом относительной несклонности к риску называется r^R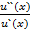(x) = - x

Будем говорить, что агент с функцией полезности u₂(x) обладает б`ольшой несклонностью к риску, чем агент с функцией полезности u1(x) , если r^A (x) < r^R(x), для любого х.

Теорема Эрроу-Пратта

Пусть предпочтения потребителей 1 и 2 представимы функциями ожидаемой полезности с возрастающими, строго вогнутыми дважды непрерывно дифференцируемыми элементарными функциями полезности. Тогда следующие утверждения эквивалентны:

1) r^A₁ (x) < r^A₂ (x)

2) u2(x) = 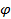(u1(x)), где 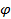– возрастающая, строго вогнутая функция

3) c2(F) < c1(F), для любой лотереи F

Будем говорить, что функция u() демонстрирует убывание абсолютной несклонности к риску, если является убывающей функцией х.

Изменение степени несклонности к риску.

Пусть предпочтения потребителя представимы функцией ожидаемой полезности с возрастающей, строго вогнутой, дважды непрерывно дифференцируемой элементарной функцией полезности. Тогда следующие утверждения эквивалентны:

1) функция u() демонстрирует убывание несклонности к риску;

2) при любом w2<w1u2(z) 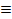u(w2 + z) является вогнутой трансформацией функции u1(z) 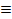u(w1+z):u2(z)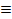 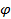(u1(z)), где φ() – возрастающая вогнутая функция;

3) для любой лотереи F величина w-c_w убывает с ростом w, где u(c_w(F)) = 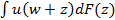.