Тема 1. Процентные вычисления
Тема 1. Процентные вычисления
Краткое содержание раздела:
Простые проценты. Cложные проценты. Кратное начисление процентов.
Непрерывное начисление процентов. Сравнение наращения по простой и сложной ставкам процента. Дисконтирование и удержание процентов. Сравнение дисконтирования по сложной и простой учетной ставкам. Эффективная учетная ставка. Мультиплицирующие и дисконтирующие множители.
“Правило 70”. Обобщение “Правила 70” . “Правило 100”. Увеличение капитала в произвольное число раз.
Влияние инфляции на ставку процента. Формула Фишера. Темп инфляции за несколько периодов.
Эффективная процентная ставка. Кратное начисление процентов. n-ый период начисления. Учет инфляции.
Эквивалентность различных процентных ставок: простых и сложных процентов, простых и непрерывных процентов, сложных и непрерывных процентов.
Внутренняя норма доходности. Внутренняя норма доходности типичных инвестиционных потоков.
Операции с валютой. Депозиты с конверсией валюты и без конверсии.
Схема 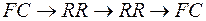 . Схема
. Схема 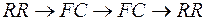
Введение
Финансовые расчеты, выполняемые в условиях определенности, называются детерминированными методами. Они имеют многовековую историю. Основу этих методов составляют расчеты, связанные с начислением простых и сложных процентов (выдача ссуды, продажа товара в кредит, учет векселя, потоки платежей и др.). Для проведения таких расчетов обычно используют методы, базирующиеся на элементарной математике. Изучению этих методов будут посвящены разделы 1 и 2.
Одним из важнейших факторов в финансовых расчетах является время. Фактор времени, особенно в долгосрочных операциях, играет не меньшую, а иногда даже большую роль, чем размеры денежных сумм. Афоризм «время - деньги»имеет давнюю историю. Он является популярным и сейчас. В его основе лежит принцип неравноценности денег, относящихся к разным моментам времени. «Сегодняшние» деньги приравниваются к возросшей денежной массе в будущем и, наоборот, вместо денег «потом» можно согласиться на уменьшенные выплаты, но сейчас. Это и составляет основание теории процента.
Влияние фактора времени многократно усиливается в период инфляции. Этот фактор часто является инструментом явного или скрытого мошенничества и недобросовестности. Очевидным следствием принципа временной неравноценности денег является неправомерность суммирования денежных величин, относящихся к разным моментам времени.
Учет фактора времени осуществляется с помощью начисления процентов или дисконтирования.
Основная терминология и обозначения
Процент
Этот термин происходит от латинского слова «pro centum», то есть «на сотню». Иными словами 1% – это сотая часть числа. Это математическоеопределение процента. Экономическое значение его более емко. В финансовой сфере слово «процент» представляет собой плату за использование денежных средств, выраженную в сотых долях от суммы долга. Таким образом, экономическое значение процента констатирует факт о том, что «за долг надо платить», а также содержит в себе количественную характеристику долга – «сколько требуется платить».
Первоначальная сумма Р– величина долга, ссуды.
Процентные деньги (проценты) I– это абсолютная величина дохода от предоставления денег в долг в любой форме.
Наращение– это процесс увеличения денег в связи с присоединением процентных денег к сумме долга Р.
Наращенная сумма S = Р+I.
Процентная ставка i –отношение суммы процентных денег, выплаченных за фиксированный отрезок времени, к величине ссуды
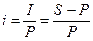 .
.
Учетная ставка d –это отношение суммы процентных денег, выплаченных за фиксированный отрезок времени, к величине наращенной суммы
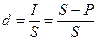 .
.
Период начисления n– интервал времени, к которому относится процентная ставка.
1.1. Простые проценты
Решение.
| P=5000000 руб. | I=Pni |
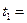 20.06.2013 20.06.2013 | 1) 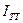 =5000000*87/365*0.15=178767 (руб.) =5000000*87/365*0.15=178767 (руб.) |
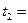 15.09.2013 15.09.2013 | 2) 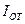 =5000000*87/360*0.15=181250 (руб.) =5000000*87/360*0.15=181250 (руб.) |
| i=15 % | 3) 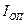 =5000000*85/360*0.15=177083,3 (руб.) =5000000*85/360*0.15=177083,3 (руб.) |
1) 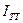 | |
2) 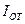 | Функция ДОЛЯГОДА |
3) 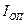 |
Решение.
| n=5 лет | 1) матем. дисконтирование: |
| S=1000000 руб. | 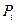 =S/(1+ni) =S/(1+ni) |
| i=20 % | 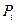 =1000000/(1+5*0.2)=500000 (руб.) =1000000/(1+5*0.2)=500000 (руб.) |
| d=20 % | 2) банковский учет: |
1) 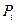 | 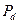 =S*(1-nd) =S*(1-nd) |
2) 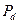 | 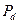 =1000000*(1-5*0.2)=0 – дисконтный множитель при простой учетной ставке быстро убывает до 0; n=5 слишком велико для такой операции. =1000000*(1-5*0.2)=0 – дисконтный множитель при простой учетной ставке быстро убывает до 0; n=5 слишком велико для такой операции. |
1.2. Сложные проценты
Решение.
| N=1 | МН=S/P – самостоятельно |
| P=2 млн.руб. | 1) 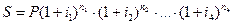 |
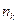 =1/4=0,25 г. =1/4=0,25 г. |  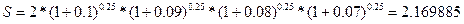 |
1) 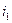 =10%, =10%, 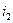 =9%,…- % сложн. =9%,…- % сложн. | 2) 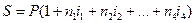 |
2) 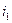 =10%, =10%, 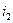 =9%,…- % прост. =9%,…- % прост. | 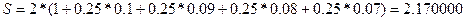 |
3)  =…= =…= 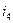 =10% - % слож. =10% - % слож. | 3) 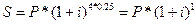 - обычное наращение по сложной ставке - обычное наращение по сложной ставке |
4) 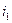 =…= =…= 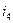 =10% - % прост. =10% - % прост. | S=2*(1+0,1)=2.200000 |
| МН, S | 4) 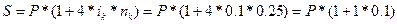 - обычное наращение по простой ставке - обычное наращение по простой ставке |
| S=2*(1+0.1)=2.200000 | |
| Комментарий: совпадение S в п.п. 3 и 4 объясняется тем, что n=1 г. |
Решение.
| n=1 | 1) 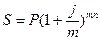 |
| P=5000000 | 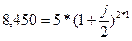 |
| m=2 | 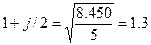 |
| S=8450000 | j=2*(1.3-1)=0.6 (60 %) |
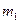 =12 =12 | 2) 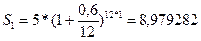 |
| 1) j | 3) 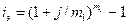 |
2) 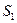 | 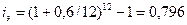 (ок. 80 %) (ок. 80 %) |
3) 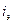 | 4) МН= 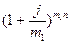 |
| 4) МН | МН= 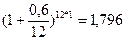 |
Обобщения «Правила 70»
1) «Правило 72» – приближенный способ расчета срока удвоения суммы вклада при фиксированной годовой процентной ставке
Срок удвоения (в годах) = 72 делить на годовую процентную ставку.
Если процентная ставка составляет от 4% до 100% годовых, то срок удвоения по «Правилу 72» вычисляется с абсолютной погрешностью, не превышающей 4%.
Если процентная ставка составляет от 1% до 15% годовых, то срок удвоения по Правилу 72 вычисляется с относительной погрешностью, не превышающей 3%.
2) Случай простых процентов.Для случая простых процентов «Правило 70» заменяется «Правилом 100», в соответствии с которым срок удвоения капитала определяется по формуле
T=100/i.
3) Кратное начисление процентов.В случае m-кратного начисления процентов за период имеем следующую формулу для срока удвоения капитала
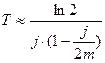 .
.
Решение.
простые проценты: 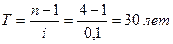 ;
;
сложные проценты: 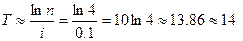 лет.
лет.
Решение.
| n=5 лет | 1) матем. дисконтирование: |
| S=1000000 руб. | 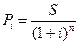 |
| i=20 % | 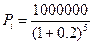 = 401877.6 (руб.) = 401877.6 (руб.) |
| d=20 % | 2) банковский учет: |
1) 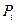 | 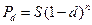 |
2) 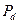 | 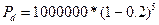 =327680 (руб.) =327680 (руб.) |
Замечание. Дисконтный множитель при сложной ставке d убывает медленнее, чем при простой. Это выгоднее для должника.
Номинальная и эффективная учетные ставки (Е.М. Четыркин, с. 56-57).
1.3. Практические приложения теории процента
(на примере простой процентной ставки)

* Последние два приложения будут рассмотрены в разделе 2.
Решение.
| n=1/2 года=6 мес. | 1) наращенная сумма без учета инфляции: |
| P=25000 руб. | 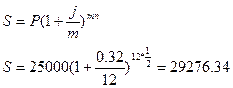 |
| j=32 % | |
| m=12 h=6% | 2) наращенная сумма с учетом инфляции: |
| С-? | 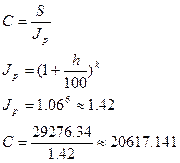 |
Формула Фишера – это формула, устанавливающая связь между темпом инфляции h, номинальной (без учета инфляции) i и реальной (с учетом инфляции) r ставками процента
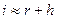 .
.
Например, если субъект положил на банковский счёт сумму денег, приносящую 10 % годовых ежегодно, то номинальная ставка составит 10 %. При уровне инфляции 6 % реальная ставка составит только 4 %.
Темп инфляции за несколько периодов.Пусть темпы инфляции за последовательные периоды времени 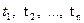 равны
равны 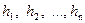 соответственно. Тогда темп инфляции
соответственно. Тогда темп инфляции 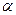 за период
за период 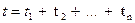 приближенно равен:
приближенно равен:
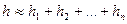 .
.
Более точное выражение имеет вид:
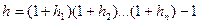 .
.
Доказательства приведенных формул можно найти в учебном пособии П.Н. Брусов и др. «Финансовая математика», с. 31.
Тема 1. Процентные вычисления
Краткое содержание раздела:
Простые проценты. Cложные проценты. Кратное начисление процентов.
Непрерывное начисление процентов. Сравнение наращения по простой и сложной ставкам процента. Дисконтирование и удержание процентов. Сравнение дисконтирования по сложной и простой учетной ставкам. Эффективная учетная ставка. Мультиплицирующие и дисконтирующие множители.
“Правило 70”. Обобщение “Правила 70” . “Правило 100”. Увеличение капитала в произвольное число раз.
Влияние инфляции на ставку процента. Формула Фишера. Темп инфляции за несколько периодов.
Эффективная процентная ставка. Кратное начисление процентов. n-ый период начисления. Учет инфляции.
Эквивалентность различных процентных ставок: простых и сложных процентов, простых и непрерывных процентов, сложных и непрерывных процентов.
Внутренняя норма доходности. Внутренняя норма доходности типичных инвестиционных потоков.
Операции с валютой. Депозиты с конверсией валюты и без конверсии.
Схема  . Схема
. Схема 
Введение
Финансовые расчеты, выполняемые в условиях определенности, называются детерминированными методами. Они имеют многовековую историю. Основу этих методов составляют расчеты, связанные с начислением простых и сложных процентов (выдача ссуды, продажа товара в кредит, учет векселя, потоки платежей и др.). Для проведения таких расчетов обычно используют методы, базирующиеся на элементарной математике. Изучению этих методов будут посвящены разделы 1 и 2.
Одним из важнейших факторов в финансовых расчетах является время. Фактор времени, особенно в долгосрочных операциях, играет не меньшую, а иногда даже большую роль, чем размеры денежных сумм. Афоризм «время - деньги»имеет давнюю историю. Он является популярным и сейчас. В его основе лежит принцип неравноценности денег, относящихся к разным моментам времени. «Сегодняшние» деньги приравниваются к возросшей денежной массе в будущем и, наоборот, вместо денег «потом» можно согласиться на уменьшенные выплаты, но сейчас. Это и составляет основание теории процента.
Влияние фактора времени многократно усиливается в период инфляции. Этот фактор часто является инструментом явного или скрытого мошенничества и недобросовестности. Очевидным следствием принципа временной неравноценности денег является неправомерность суммирования денежных величин, относящихся к разным моментам времени.
Учет фактора времени осуществляется с помощью начисления процентов или дисконтирования.
