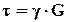Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига.

Пусть прямоугольный элемент, выделенный в окрестности некоторой точки, испытывает только деформации сдвига.Удлинения его сторон отсутствует.

Рассечем данный элемент наклонной площадкой.

Изобразим напряжения, действующие на нее в условиях чистого сдвига.

Если угол α будет равен нулю, то площадка становиться то горизонтальной гранью нашего элемента, если 90 градусов то вертикальной гранью.

Рассмотрим равновесие отсеченной части данного объема.

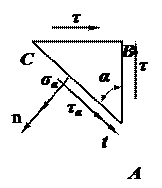По граням будут действовать касательные напряжения τ.

На наклонной площадке в зависимости от угла α возможно возникновение как нормального, так и касательных напряжений.

Изобразим нормаль. Вектор полного напряжение раскладывается на нормальное σ_α и касательное τ_α.

В направлении нормали будет действовать нормальное напряжение σ_α. Перпендикулярно нормали вдоль наклонной грани касательное τ_α.

Проектируем все силы, действующие на призму, на оси n и t.

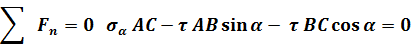
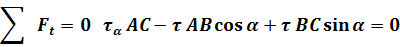
откуда

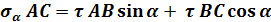
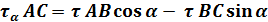
Отрезки АВ и АС вычислим из прямоугольного треугольника.

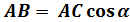
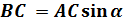
Т.о. при повороте площадки на угол α нормальные напряжения σ_α, и тангенциальные τ_α будут определяться по следующим формулам:

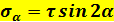
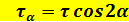
Анализируя эти формулы получаем

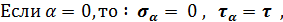
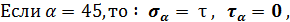
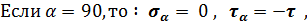
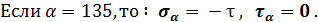
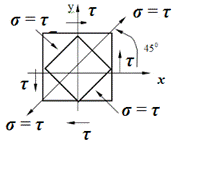
Таким образом, на площадках, ориентированных под углом 45 и 135 градусов к первоначальным, действуют только нормальные напряжения, равные по величине касательным, но противоположные по знаку.

Следовательно, если из пластины выделить прямоугольный элемент, грани которого повернуты относительно исходных плоскостей на угол 45 градусов, то на секущих площадках будут обнаружены только нормальные напряжения, причем на одной паре граней эти напряжения являются растягивающими, а на другой – сжимающими.

Т.о., чистый сдвиг может быть представлен как одновременное растяжение и сжатие по двум взаимно перпендикулярным направлениям.

Чистый сдвиг представляет собой единственный вид напряжённого состояния, при котором отсутствует изменение объёма материала, а выделенный элемент изменяет только форму

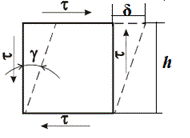Деформация сдвига характеризуется γ - углом сдвига или относительным сдвигом.

Этот параметр не зависит от расстояния 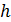на которое происходит сдвиг.

Величина δ на которую смещается грань называют абсолютным сдвигом

Относительный сдвиг выражается в радианах.

Определим относительный сдвиг.

Из рисунка видно , что угол сдвига γ пропорционален касательным напряжениям.

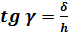
Вследствие малости деформации, угол относительного сдвига 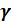мал, следовательно, можно принять

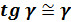
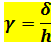
Относительный сдвиг будет равен абсолютному сдвигу на высоту.

Закон Гука при сдвиге.

В предыдущей лекции мы уже формулировали закон Гука, напряжение пропорционально деформации, следовательно, для касательных напряжений и соответствующего им сдвига можно записать.