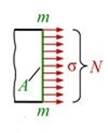
При растяжении - сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению.

Через данную точку тела можно провести бесчисленное множество сечений, различно ориентированных в пространстве. Возникающие в них напряжения будут различны. Поэтому нельзя говорить о напряжении в данной точке, не указывая площадки (сечения), на которой это напряжение возникает.

Совокупность нормальных и касательных напряжений, возникающих во всем бесчисленном множестве различно ориентированных площадок, которые можно провести через заданную точку, характеризуют напряженное состояние в этой точке.

Рассмотрим элемент бруса, который растягивают.

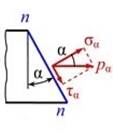
Рассечем брус двумя плоскостями, одну перпендикулярно оси, вторую под углом α. Мы уже знаем , что при растяжении - сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению.

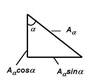
Проведем анализ напряженного состояния наклонного сечения n-n.

Мы обозначили площадь поперечного сечения m-m А.

Площадь Аα наклонного сечения больше площади А поперечного сечения, т к является гипотенузой в прямоугольном треугольнике.

где - площадь наклонного сечения,

А - площадь поперечного сечения,

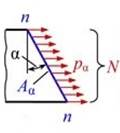
Определим напряжения на площадке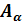

Рассмотрим участок наклонной площадки.

,

Разложим вектор напряжения 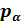на две составляющие– нормальную σ_α направленную перпендикулярно сечению и касательную τ_α

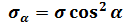
Воспользовавшись формулами тригонометрии

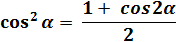
получим

Аналогично найдем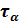

Окончательно

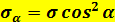
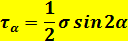
Изменяя угол наклона площадки Aα, получим максимальные и минимальные напряжения:

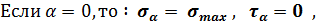т.е. напряжения действуют в поперечном сечении

, т.е напряжения в продольном сечении отсутствуют. Продольные слои растянутого стержня не имеют друг с другом силового взаимодействия.

Растяжение бруса можно рассматривать как растяжения пучка параллельных нитей не связанных друг с другом.

- касательное напряжение на этой площадке имеет максимальное значение.

Выводы:

1. Максимальное нормальное напряжение возникает в сечениях, перпендикулярных продольной оси.

Продольные волокна стержней не давят друг на друга в направлении осей поперечного сечения.

3. Максимальное касательное напряжение возникает на площадках, наклоненных под углом45º к продольной оси стержня.

Напряжения во взаимно перпендикулярных площадках.

Выясним, какая существует связь между напряжениями, действующими во взаимно перпендикулярных площадках.

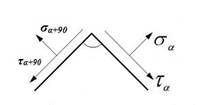
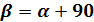
Сравнивая зависимости получаем:

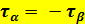
Таким образом, касательные напряжения во взаимно- перпендикулярных площадках равны по величине, но противоположны по знаку. Это положение носит название закона парности касательных напряжений.

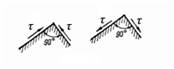
Чистый сдвиг

Рассмотрим элементарный объем в окрестности любой точки тела, подвергающейся сдвигу см. рис.

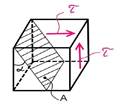Напряженное состояние, при котором на гранях выделенного элемента возникают только касательные напряжения τ , называется чистым сдвигом.