Трудности детерминизма

Все же постулирование детерминизма природы представляет собой лишь самый общий принцип научного объяснения, принцип, согласно которому природу сле­дует рассматривать исключительно как сумму эффектов, механически детермини­рованных хронологически предшествующи­ми причинами. Разумеется, такой принцип слишком общ, чтобы самостоятельно да­вать объяснение конкретных фактов. Поэ­тому нужно, путем детального исследова-

³ Кант И. Критика практического разума. Ч. 1. Кн. 1. Гл. 3. Критическое освещение аналити­ки... // Соч.: В 6 т. М., 1965. Т. 4. Ч. 1. С. 425—426.

ния и прежде всего наблюдения, вскрывать конкретные механизмы, действующие в тех или иных явлениях, и контролировать объ­яснение с помощью систематического экс­периментирования:

Пробегая мысленным взором предметы, которые когда-либо представлялись моим чувствам, я смею сказать, что не заметил ни одной вещи, которую бы я не мог без особого труда объяснить с помощью най­денных мною начал. Но я должен также сознаться, что могущество природы прос­тирается так далеко, а начала мои так просты и общи, что мне не представляется никакого частного следствия, которое не могло бы быть выведено из начал нес­колькими различными способами, так что самым трудным для меня было найти, каким способом лучше всего выразить эту зависимость. Ибо тут я не знаю другого приема, как вновь подобрать несколько опытов...¹

В этом обращении к эксперименту заклю­чается превосходство современной науки над наукой античной, и это соответствует существенной практической направленнос­ти науки нового времени. Действительно, экспериментирование связано с движением "от следствий к причинам", то есть от на­блюдения естественных следствий к пред­ставлению о производящих их механизмах, позволяя, таким образом, "обратить... на пользу"² естественные процессы.

Однако такая концепция научного объ­яснения позволяет прийти лишь к ограни­ченным и частичным истинам, таким, как открытые Галилеем законы падения тел, как объяснение Паскалем барометрических явлений тяжестью воздуха и т. п. Конечно, эти частные исследования приводят и к важным обобщениям в механике твер­дых тел или жидкостей. Тем не менее меж­ду общим принципом детерминизма при­роды и объяснением фактов остается ог-ромная дистанция, которую стремятся заполнить объяснительные теории.

Таким образом, если проследить реаль­ное историческое развитие современной на­уки, то будет видно, что принцип детер­минизма получает непосредственно экспе­риментальное подтверждение лишь на уровне наблюдений и опытов, "которые са-

' Декарт Р. Рассуждение о методе... Ч. 6 // Соч. Т. 1. С. 287—288. ² Там же. С. 287.

ми представляются нашим чувствам и о ко­торых мы не можем оставаться в неведении при малейшем о них размышлении"³: ша­рик, катящийся по наклонной плоскости, подъем воды в вакуумном насосе и т. д. Но уже с XVII века делаются попытки довести научное объяснение до познания скрытых механизмов природы с тем неизбежным по­следствием, что предлагаемые на этом уровне объяснения не могут получить под­линного подтверждения в опыте. Хорошим примером такого оборота дел служит фи­зическая оптика. Еще в 1632 году⁴ Декарт разработал объяснение природы света, ко­торое смогло подвергнуться эксперимен­тальной проверке лишь в 1830 году. Таким образом, в течение двух веков в оптике выдвигались одна за другой объяснитель­ные теории, не имевшие прямого экспери­ментального подтверждения. В результате эти теории могли разрабатываться лишь в крайне абстрактной форме, отражавшей на материале механики света противоречия математического представления простран­ства как прерывного или непрерывного. Поэтому неудивительно, что эксперименти­рование обнажило противоречие и показа­ло неудовлетворительность такого типа объяснений.

а) Механика частиц и механика волн

В те времена, когда Декарт разрабаты­вал свою теорию света, были уже известны основные факты, касающиеся передачи све­та в пространстве. Знали, что в прозрачных средах свет распространяется по прямой линии; что если он отражается от поверх­ности (например, зеркала), то угол падения равен углу отражения; что если он перехо­дит из одной прозрачной среды в другую, то его траектория изменяется (преломле­ние), причем синус угла преломления (то есть угол, образуемый преломленным ра­диусом и нормалью к поверхности прелом­ления в точке преломления) остается всегда пропорциональным синусу угла падения:

'Там же.

"Год окончания "Мира" и начала работы над "Диоптрикой".

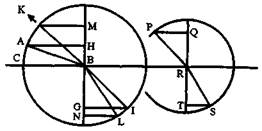
Например, если луч идет по воздуху от А к В и, падая в точке В на поверхность стекла CBR, отклоняется к I в этом стекле; и если другой луч идет от К к В и отклоня­ется к L; и третий идет от P к R и отклоня­ется к S, то между линиями КМ и LN или PQ и ST должно быть такое же соотноше­ние, как и между АН и IG, но между углами КВМ и LBN или PRQ и SRT — не такое же, как между АВН и IBG¹.

Но эти законы были установлены чисто эмпирическим образом. Так, прямолинейное распространение света — это повседневно наблюдаемый факт; закон отражения фигури­рует в качестве постулата в "Оптике", появив­шейся в античности под именем Евклида; а закон преломления был установлен путем индукции на основе измерений голландцем Снеллиусом. Декарт же ставит перед собой задачу перейти от простого наблюдения фак­тов и от управляющих ими законов к объяс­нению их причин через выявление естествен-ного механизма, скрытого за явлениями.

Для этого он отождествляет свет с дейст­вием световой частицы, проходящей через прозрачные тела так, что ее движению не мешают "грубые части"², из которых эти тела состоят. К такой частице можно приме­нить законы механики во всей их математи­ческой чистоте, так как ее можно отождест­вить с телом, законы движения которого нам известны, например с мячом для лапты, но при этом абстрагируясь от всей сложно­сти движения реального тела. Действитель­но, можно предположить, что "скорость мяча постоянна", пока он остается в одной и той же прозрачной среде, и что не надо учитывать "ни следствия его веса, величины или формы"³:

¹ Descartes R. Dioptrique. Discours second. (См. также: Декарт Р. Диоптрика. Гл. II // Де­карт Ренэ. Рассуждение о методе. С приложени­ями "Диоптрика", "Метеоры", "Геометрия". М., 1953. С. 85—86.)

² Ibidem.

³ Декарт Р. Диоптрика. Гл. II. С. 78.

Ибо здесь не преследуется цель детально разбирать данный случай, тем более что ни один из названных факторов не имеет значения при воздействии на свет, к кото­рому должно было бы относиться все ска­занное выше⁴.

Только приняв эти допущения, становится возможным объяснить механическим обра­зом законы, вытекающие из наблюдения.

Так, отражение может быть объяснено как результат отскока частицы света, — отождествленной с простой материаль­ной точкой, — от поверхности, которая "совершенно плоска и тверда"⁵:

"Итак, представим себе, что мяч, брошен­ный от А к В, ударяется в точке В о по­верхность земли СВЕ, которая, не позво­ляя ему двигаться дальше, становится причиной того, что он отскакивает; и по­смотрим, в какую сторону".

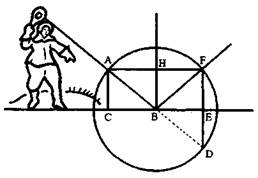
"Двигательную детерминацию" у летяще­го мяча можно "разложить на части, из которых, как можно себе представить, она состоит": она раскладывается на перпен­дикулярную составляющую и параллель­ную к поверхности отражения. "Легко по­нять, что встреча" с этой поверхностью "может воспрепятствовать лишь одной из этих детерминаций" — "той, которая за­ставляла мяч двигаться вниз от AF к СЕ", а не другой, "заставлявшей его двигаться направо". "Опишем окружность с центром в В, проходящую через точку А". Если мы предполагаем, что скорость полета мяча остается постоянной, то точки этой ок­ружности — это те точки, которые мяч, отскакивающий в точке В, может достичь за то же время, "которое было затрачено на движение от А к В". "Затем, чтобы выяснить, к какой именно из этих точек должен направиться отскочивший мяч, проведем три прямые линии — АС, НВ

⁴ Там же. С. 78—79.

⁵ Там же. С. 78.

и FE, перпендикулярные к СЕ, и таким образом, чтобы между АС и НВ расстояние было не больше и не меньше, чем между НВ и FE". Поскольку составляющая движения параллельная к поверхности отражения предполагается постоянной, то "за то же время, за какое мяч продвинулся направо от точки А — одной из точек линии АС

— до точки В — одной из точек линии НВ, он должен продвигаться дальше линии H В

— до какой-либо точки линии FE". Таким образом, на пересечении окружности с центром В и радиусом AB и прямой FE¹ находятся точки, которых должен достичь мяч, двигающийся из В, за столько же времени, за сколько он прошел от А до В. "А поскольку земля не дает ему двигаться к точке D, следует заключить, что мяч должен неминуемо идти к точке F"².

Таково доказательство известного положе­ния о равенстве угла падения углу отражения. Таким же способом можно доказать за­кон преломления, сравнивая переход части­цы света из прозрачной среды в другую с изменением траектории мяча, когда он наталкивается на "кусок материи СВЕ, ко­торая настолько слаба и редка, что он мо­жет прорвать ее и пройти насквозь, теряя только часть своей скорости"³:

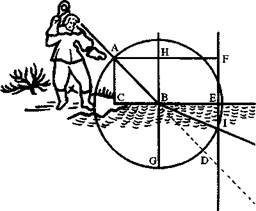
Если разложить "двигательную детерми­нацию" летящего мяча на две составляю­щих, одну перпендикулярную, а другую параллельную к поверхности преломле­ния, то "лишь та, которая направляет мяч

сверху вниз, может быть каким-то обра­зом изменена вследствие столкновения с полотном". Предположим, что мяч, про­ходя через полотно, теряет, скажем, поло­вину своей скорости. Тогда, "проведя из центра В окружность AFD и возведя на линии СВЕ под прямым углом три пря­мых линии — АС, НВ и FE, так, чтобы расстояние между FE и H В было вдвое больше, чем между НВ и АС, мы увидим, что этот мяч должен двигаться к точке I. Ибо, раз он теряет половину скорости, проходя через полотно СВЕ, ему необхо­димо вдвое больше времени, чтобы прой­ти нижнюю часть от точки В до какой-то точки на окружности AFD, чем ему потре­бовалось для прохождения верхней части от А до В. А поскольку он ничего не теряет от той детерминации, которая по­буждала его двигаться в правую сторону, то за вдвое большее время, чем ему пона­добилось, чтобы пройти от линии АС до линии НВ, он должен проделать вдвое больший путь в эту самую сторону и, следовательно, дойти до какой-то точки прямой FE в тот же момент, когда он доходит также до какой-то точки окруж­ности AFD. Но это было бы невозможно, если бы он не двигался к точке Г'⁴.

Отсюда видно, что "соотношение или про­порция между углами" падения и рефрак­ции "меняется при различных наклонах лу­чей"⁵, тогда как отношение между синуса­ми остается постоянным.

Опыт, однако, показывает, что не так просто истолковать преломление света, ис­ходя из анализа механического движения мяча:

Но, может быть, вы удивитесь, произведя опыты, что лучи света, достигнув поверх­ностей, где совершается их преломление, больше наклоняются в воздухе, нежели в воде, и еще сильнее в воде, чем в стекле, в противоположность тому, что происхо­дит с мячом, который больше наклоняется в воде, чем в воздухе, и совсем не может проникнуть в стекло⁶.

В самом деле, если рассмотреть чертежи, построенные на основе опыта, то приходит­ся признать, что если скорость мяча замед­ляется при переходе из воздуха в воду, то света — ускоряется:

¹ Точнее, прямой FD. — Примеч. ред. ^г Descartes R. Dioptrique. Discours second. Resume.

¹ Декарт Р. Диоптрика. Гл. II. С. 81.

⁴ Descartes R. Dioptrique. Discours second. Resume.

⁵ Descartes R. Dioptrique. Discours second.

⁶ Декарт Р. Диоптрика. Гл. II. С. 87.

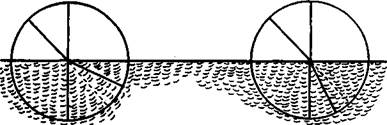I. Переход мяча из воздуха в воду.

2. Переход света из воздуха в воду.

Чтобы объяснить этот парадокс, Декарт вынужден сослаться на структуру невиди­мых частиц воздуха и воды:

Мяч в своем движении теряет больше, когда он ударяется о мягкое тело, нежели о твердое, и что он катится менее легко по ковру, чем по непокрытому столу; таким образом, действие разреженной материи может значительно сильнее ос­лабляться частицами воздуха, которые, будучи мягкими и слабо сцепленными, мало ему сопротивляются, нежели час­тицами воды, которые больше ему со­противляются, и еще сильнее частицами воды, чем частицами стекла или хру­сталя¹.

Стало быть, по Декарту, мягкость частиц воздуха объясняет замедление скорости света. Но, не говоря уже о чисто во­ображаемом характере этой гипотезы, она неприемлема с физической точки зрения:

Если верно, что воздух вследствие своей гибкости отнимает часть силы, как и ко­вер, по которому катится шарик, эта сила не будет возвращена, когда луч выходит из воздуха и уходит в воду².

Если замедление скорости света в воздухе может быть объяснено просто структурой частиц воздуха, то, с другой стороны, структура частиц воды не может дать им­пульс к ускорению.

В результате сразу же после Декарта Гюйгенс предложил другую трактовку оп­тических явлений. Разумеется, он признает,

что "нельзя сомневаться в том, что свет состоит в движении какого-то вещества"³. Но отсюда нельзя заключать, что это дви­жение можно изобразить как движение "пу­ли или стрелы"⁴, проходящих сквозь воз­дух. Это оказывается несовместимым с тем фактом, что лучи света, идущие от разных источников, способны проходить "один че­рез другой, не мешая друг другу"³. Поэ­тому объяснение движения света надо ис­кать в другом способе передачи движений и, в частности, основываясь на том, "что нам известно о распространении звука в воздухе"⁶.

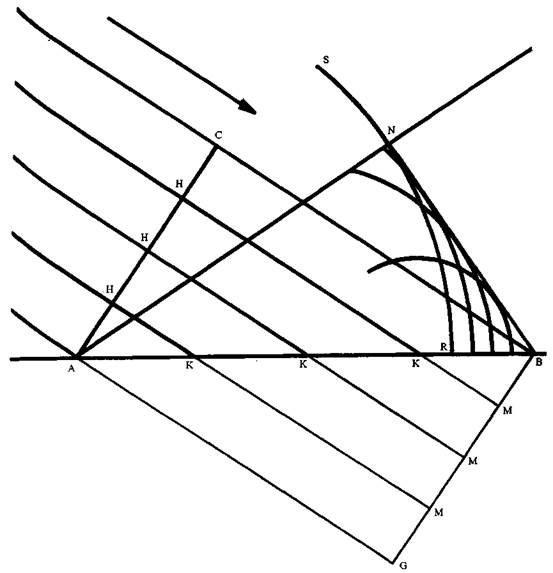
Дело в том, что прохождение звука через воздух (как и распространение ударной волны в воде) представляет собой такую форму движения, при которой нет переме­щения движущегося тела: удар распростра­няется через вещество так, что оно не меня­ет своего местонахождения. Это явление иллюстрируется передачей ударов тверды­ми телами:

Если взять несколько одинаковых по вели­чине шаров, сделанных из какого-нибудь очень твердого вещества, и если их рас­положить по прямой линии так, чтобы они касались друг друга, то при ударе таким же шаром по первому из них ока­жется, что движение как бы в одно мгно­вение передается до последнего шара, ко­торый и отделяется от всего ряда, причем не заметно, чтобы при этом сдвинулись остальные шары'.

¹ Декарт Р. Диоптрика. Гл. II. С. 88.

² Leibniz G. G. Lettre ä Molanus (?) // Die philosophischen Schriften von G. W. Leibniz. Hrsg. von C. J. Gerhardt. Berlin, 1882. Bd. IV. S. 308.

³ Гюйгенс X. Трактат о свете. Гл. 1. М.; Л., 1935. С. 11.

⁴ Там же. С. 12.

⁵ Там же. 'Там же. ⁷ Там же. С. 23.

Простые опыты показывают, что удары мо­гут не только передаваться по прямой линии, но и расходиться веером по твердым телам:

Если шар, который, как, например, шар А, прикасается к нескольким другим одина­ковым с ним шарам ССС, толкнуть дру­гим шаром В, то шар А будет действовать на все соприкасающиеся с ним шары ССС и передаст им все свое движение; сам же он, как и шар В, останется после этого неподвижным¹.

Таким образом, Гюйгенс представляет се­бе, что свет распространяется, подобно удару, через невидимые, но абсолютно твердые частицы субстанции, которую он называет "эфиром"².

На первый взгляд кажется, что на основе этой гипотезы трудно объяснить передачу света по прямой линии, представляющуюся несовместимой с его передачей волновым путем:

Каждая частица вещества, в котором рас­пространяется волна, должна сообщать свое движение не только ближайшей час­тице, лежащей на проведенной от светя­щейся точки прямой, но необходимо сооб­щает его также и всем другим частицам, которые касаются ее и препятствуют ее движению. Таким образом, вокруг каждой частицы должна образоваться волна, центром которой она является³.

'Гюйгенс X. Трактат о свете. Гл. 1. С. 26—27.

² Это слово по-гречески обозначает светящу­юся область неба — ту, которая на заре загора­ется первой.

³ Гюйгенс X. Трактат о свете. Гл. 1. С. 31.

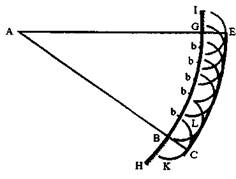
Рассмотрим, однако, волну, исходящую из пункта А и доходящую до отверстия BG, ограниченного непрозрачными перегород­ками НВ и GI. Верно, что в точке В возника­ет небольшая волна KCL, так же как и во всех точках b, b, b волны BG. Но это все маленькие волны, каждая из которых может быть только "бесконечно слабой"⁴, так что их действие становится ощутимым лишь там, где они все вместе "содействуют обра­зованию волны, заканчивающей движение", то есть "на окружности СЕ, их общей каса­тельной линии", и "ясно, что только точка С волны KCL, то есть та, которая находит­ся на прямой, проведенной через AB, кос­нется волны" СЕ⁵. Волна света, исходящая из А и проходящая через отверстие BG, всегда будет ограничиваться "прямыми АС, АЕ", так как "части отдельных волн, выхо­дящие за пределы пространства АСЕ, будут слишком слабы, чтобы давать свет"⁶.

Эта гипотеза относительно построения малых волн позволяет выдвинуть геомет­рическое доказательство отражения света:

Пусть AB будет плоская и полированная поверхность какого-нибудь металла, стек­ла или другого тела... и пусть прямая АС, наклонная к AB, представляет собой часть световой волны, центр которой будет так далеко, что эта часть АС может быть при­нята за прямую линию... Точка С волны АС в некоторый промежуток времени про­двинется до плоскости AB к точке В по прямой СВ, которую должно представ­лять себе исходящей из светящегося цен­тра и которая, следовательно, перпендику­лярна к АС. Но за тот же промежуток времени точка той же волны А не могла

"Там же.

⁵ Там же. С. 33, 31.

'Там же. С. 31.

но крайней мере, отчасти — сообщить свое движение за пределы плоскости AB и должна была продолжить свое движение в материи, находящейся над этой плоско­стью, притом на протяжении, равном СВ; вместе с тем она должна была, согласно сказанному выше, образовать свою отдель­ную сферическую волну. Указанная волна изображена здесь окружностью SNR, центр которой в А, а полудиаметр AN равен СВ. Если затем рассмотреть остальные точки H волны АС, то ясно, что они не только достигнут поверхности AB по прямым НК, параллельным СВ, но еще породят

в прозрачной среде из центров К отдель­ные сферические волны, представленные тут окружностями, полу диаметры которых равны линиям КМ, т. е. продолжениям линий НК до прямой BG, параллельной АС. Но все эти окружности... имеют общей касательной прямую BN... Поэтому... BN является распространением волны АС в тот момент, когда ее точка С достигла точки В... Но отсюда видно, что угол отражения оказывается равным углу падения. Из то­го, что треугольники АСВ и BNA прямо­угольны и имеют общую сторону AB, а сторона СВ равна NA, следует, что углы,

противолежащие этим сторонам, будут равны, а следовательно, также углы СВА и NAB. Но как СВ, перпендикулярная к СА, показывает направление луча пада­ющего, так AN, перпендикулярная волне BN, показывает направление луча отра­женного; значит, эти лучи одинаково на­клонены к плоскости AB¹.

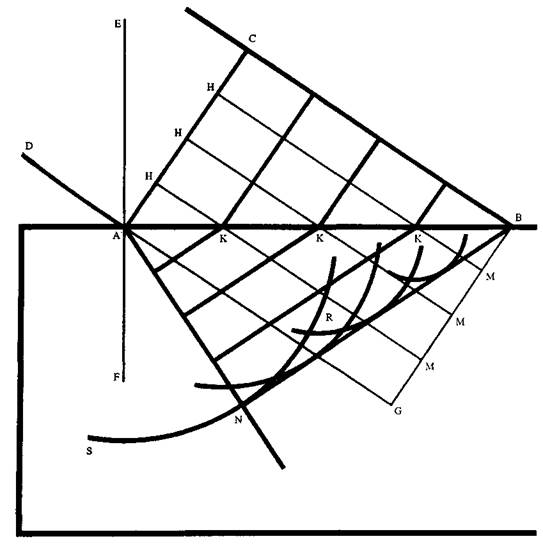
На основе тех же принципов строится до­казательство закона преломления:

...Допустим, что прямая AB представляет собой плоскую поверхность, которой ог­раничены прозрачные тела, простирающи-

¹ Гюйгенс X. Трактат о свете. Гл. 2. С. 36—39.

еся по направлению к С и к N... Пусть линия АС представляет собой часть световой вол­ны, центр которой, по предположению, так далек, что эту часть можно рассматривать как прямую линию. Тогда точка С волны АС в некоторый промежуток времени до­стигнет плоскости AB по прямой СВ, кото­рую нужно представлять себе исходящей из светящегося центра и которая, следователь­но, пересечет АС под прямыми углами. Если бы материя прозрачного тела передавала движение волны так же быстро, как материя эфира, то за это же время точка А пришла бы в точку G по прямой АО, равной и парал­лельной СВ, и вся часть волны АС оказалась бы в GB. Но предположим, что она передает

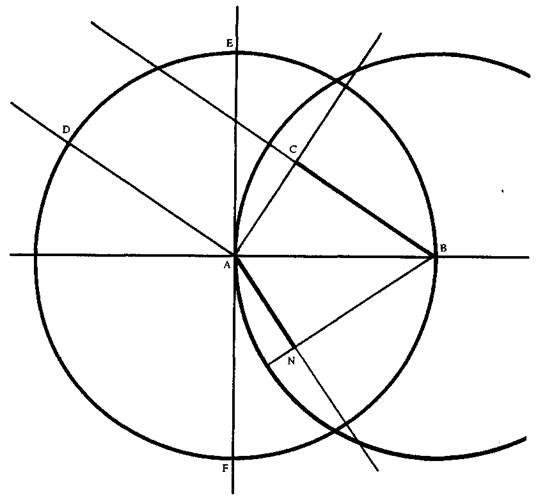это движение менее быстро, скажем, на одну треть. Тогда от точки А движение распро­странится в материи прозрачного тела на расстояние, равное двум третям СВ, образо­вав свою отдельную сферическую волну, согласно сказанному выше; эта волна изо­бражена окружностью SNR, центр которой А, а полудиаметр равен двум третям СВ. Далее, если рассматривать другие точки H волны АС, то окажется, что за то время, за которое точка С придет в В, они не только достигнут поверхности AB по прямым НК, параллельным СВ, но сверх того произведут еще из центров К в прозрачной среде от­дельные волны, представленные здесь ок­ружностями, полудиаметры которых равны двум третям линий КМ, т. е. двум третям продолжений линий НК до прямой BG; эти полудиаметры были бы равны целым КМ,

если бы обе прозрачные среды были одина­ковой проницаемости. Следовательно, все эти окружности имеют общей касательной прямую линию BN, т. е. ту линию, которая служила касатель­ной из точки В к окружности SNR... И зна­чит, эта прямая... является распростране­нием волны АС в тот момент, когда ее точка С достигла точки В¹.

Отсюда следует, что синус угла падения (DAE) при любом наклоне луча DA со­храняет одинаковое отношение к синусу уг­ла преломления (NAF) и что это отношение равно отношению скоростей волн в двух прозрачных средах:

¹ Гюйгенс X. Трактат о свете. Гл. 3. С. 51—53.

Если... провести прямую EAF, которая пе­ресекла бы плоскость AB под прямыми углами в точке А, и если линия AD будет перпендикулярна к волне АС, то линия DA будет обозначать падающий луч света, а прямая AN, перпендикулярная к BN, — луч преломленный... Если принять AB за радиус круга, то синусом угла ВАС будет ВС, а синусом угла ABN будет AN. Но угол ВАС равен углу DAE, так как каждый из них, прибавленный к углу САЕ, образует прямой угол. Угол же ABN равен углу NAF, так как каждый из них образует прямой угол вместе с углом BAN. Следова­тельно, синус угла DAE относится к синусу угла NAF, как ВС к AN. Но отношение ВС к AN было равно отношению скоростей света в материи, находящейся в направле­нии к АЕ, и в материи, направленной к AF; таким образом, синус угла DAE относится к синусу угла NAF, как указанные скорости света¹.

Мы видим, что, по гипотезе Гюйгенса, изо­бражение перехода света из воздуха в воду получается соответствующим эмпиричес­ким наблюдениям, если предполагается, что скорость света в воде меньше, чем в воздухе.

Таким образом, гипотеза Декарта, осно­вывающаяся на корпускулярной, или дис­кретной, концепции материи, и гипотеза Гюйгенса, предполагающая волновую, или непрерывную, передачу движения, приводят к прямо противоположным следствиям. Дей­ствительно, из гипотезы Декарта можно заключить, что скорость света в воде больше, чем в воздухе, а из гипотезы Гюйгенса выхо­дит, что в воздухе она больше, чем в воде.

Но до XIX века экспериментальное срав­нение света в воздухе и в воде выходило за рамки технических возможностей. Поэтому в течение двух столетий корпускулярная и волновая теории соперничали между собой в условиях, когда, не имея прямого подтвер­ждения со стороны опытных данных, они соотносились с опытом лишь через посредст­во сложных и сомнительных умозаключений.

Главным возражением против корпуску­лярной гипотезы Декарта была ее неспосо­бность объяснить ускорение света, которое должно было возникать при его переходе из воздуха в воду. Решение этой проблемы предложил Ньютон, исходя из теории все­общего тяготения. Если предположить, что корпускулы, из которых состоит вода, рас-

' Гюйгенс X. Трактат о свете. С. 54—55.

положены ближе друг к другу, чем корпу­скулы воздуха (что соответствует ее боль­шей плотности), то они должны создавать более сильное притяжение, способное объ­яснить эффект ускорения. Приняв корпуску­лярную теорию, Ньютон привел к единству физические исследования, поскольку в оп­тических явлениях он усматривал действие тех же основных законов, что и в небесной механике. Это преимущество в унификации науки, соединенное с авторитетом Ньюто­на, привело к тому, что корпускулярная оптика получила почти всеобщее признание у его современников и преемников.

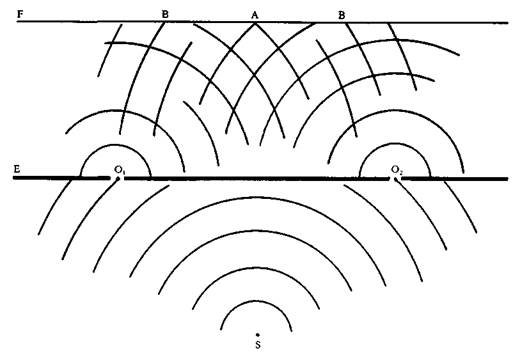
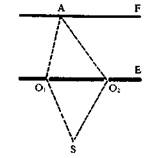
Между тем корпускулярная теория ос­тавляла необъясненными некоторые явле­ния, известные уже в эпоху Ньютона и под­дающиеся объяснению на основе волновой теории света. Самым интересным с точки зрения дальнейшей теоретической разра­ботки являлось, несомненно, явление ин­терференции. Предположим, что перед све­товым источником (S), испускающим мак­симально однородный свет, расположен экран с двумя отверстиями (Οι и Ог). Тогда, если за этим экраном (Е) поставить второй экран (F), то на нем будут наблюдаться чередующиеся темные и светлые полосы, причем последние по мере удаления от цен­тра будут становиться все темнее и под конец сольются с окружающей темнотой. Согласно волновой теории, это явление объясняется следующим образом: ярко ос­вещенные полосы соответствуют наложе­нию двух максимальных колебаний (или вершин двух волн — А), тогда как темные — наложению максимального колебания на минимальное (или вершины одной вол­ны на впадину другой — В), что приводит к их взаимному погашению. (См. рисунок на с. 335. — Ред.}

Что же касается корпускулярной теории, то она так и не смогла дать объяснение этого явления исходя из своих собственных посылок. Все же возможность найти такое объяснение оставалась открытой до тех пор, пока в 1850 году Фуко, измерив скоро­сти света в воздухе и в воде, не обнаружил, что в воде свет движется медленнее. С это­го момента речь уже шла не просто о странном явлении, плохо увязывающемся с основными объяснительными гипотезами корпускулярной теории, каковым было яв-

ление интерференции. Теперь налицо име­лось прямое и явное противоречие с этими гипотезами. В результате, на основе экспе­римента Фуко, корпускулярная теория бы­ла отброшена и восторжествовала исклю-чительно волновая теория.

Однако волновое описание световых про­цессов натолкнулось на препятствие в виде явления фотоэффекта. Когда пучок световых или ультрафиолетовых лучей падает на ме­таллическую пластинку, из нее вылетают электроны, движущиеся с большей или мень­шей скоростью. Чтобы объяснить это явле­ние, допускают, что энергия световых волн превращается в кинетическую энергию дви­жения электронов. Это движение может быть более или менее быстрым, но его скорость "зависит не от интенсивности излучения, а только от длины волны, т. е. от цвета лучей, причем эта скорость тем больше, чем короче длина волны"¹. Такой факт представ­ляет "серьезную опасность" для "волновой

теории Гюйгенса"². В самом деле, по волно­вой теории, свет рассеивается непрерывным образом. Чем больше удаление от светового источника, тем больше становится поверх­ность сферической волны и, следовательно, тем больше должна уменьшаться энергия, содержащаяся в той части этой поверхности, которая доходит до металлической пластинки:

2Тамже. С. 131.

¹ Планк М. О природе света // Планк М. Единство физической картины мира. М., 1966. С. 132.

Таким образом, эта энергия должна бы­ла бы, быстро уменьшаясь, стать ниже ми­нимальной величины, необходимой для ее преобразования в кинетическую энергию электронов. Но вместо этого обнаружива­ется, что "если отодвигать металл на все большее расстояние от источника света... то электроны продолжают вылетать с та­кой же самой скоростью, несмотря на более слабое освещение"¹. Что уменьшается при ослаблении интенсивности света, так это количество электронов, вылетающих за единицу времени. Эти факты, по-видимому, свидетельствуют о том, что световая энер­гия никогда не опускается ниже какой-то минимальной величины. А это значит, что свет предстает в прерывистой форме — в виде зернышек света, говоря образным языком, — но не в виде непрерывной вол­ны. В результате теория света, благодаря работам Планка начала XXвека, была объ­единена с так называемой "квантовой" тео­рией, согласно которой энергия в ее различ­ных формах никогда не опускается в приро­де ниже определенной минимальной величины и, следовательно, обладает пре­рывистой структурой.

Квант, или минимальное количество световой энергии, называется фотоном. Можно подумать, что сведение света к фо­тонам — это возврат к корпускулярной теории света, как ее разрабатывали Декарт и Ньютон. Однако наблюдаемые факты и их теоретическая интерпретация не дают основания для простого возврата к корпу­скулярной механике, поскольку она оказы­вается неспособной объяснить такие явле­ния, как интерференция. Действительно, со­гласно корпускулярной теории явление интерференции должно истолковываться следующим образом: яркие полосы на эк­ране — это те части экрана, на которые попадают фотоны. Рассмотрим путь фото­на, вышедшего из источника S и попадаю­щего на экране F в точку А. Исходя из правил механики корпускул, следует спро­сить, через какое из двух отверстий экрана E прошел фотон. Экспериментальная физи­ка знает лишь один способ, как ответить на этот вопрос: закрыть одно из отверстий

¹ Планк М. О природе света // Планк М. Единство физической картины мира. С. 132.

и посмотреть, какие яркие полосы станут темными на экране F. Результат же этого опыта таков: в месте чередующихся свет­лых и темных полос появляются концен­трические кольца, попеременно светлые и темные, которые на внешних краях слива­ются с окружающей темнотой².

Различие результатов в зависимости от того, имеется ли в экране, находящемся перед источником света, одно или два отверстия, очевидно, не может быть объяс­нено при помощи корпускулярной гипо­тезы. Ведь согласно этой гипотезе закры­тие одного из отверстий должно было бы воспрепятствовать прохождению полови­ны фотонов; отсюда должны были бы получиться на втором экране темные зоны, так что если открыть оба отверстия, то общее распределение светлого и темно­го "должно быть точной суммой" рас­пределений в случае открытия одного, а затем другого отверстия³. То, что получаемый результат оказывается совер­шенно разным в случае открытия одного или двух отверстий, несовместимо с кор­пускулярной механикой, по которой, в слу­чае открытия обоих отверстий, следовало бы допустить или что фотон "может разделиться и пройти сквозь оба отвер­стия", или что "отверстие, сквозь которое фотон не проходит"⁴, изменяет его траек­торию, — допущения, разумеется, гораздо менее приемлемые, чем волновая интер­претация. Таким образом, сами факты приводят нас к следующему выводу: если

² См.: Эйнштейн А. и Инфельд Л. Эволюция физики. Волновая теория света. М., 1956. С. 127.

³ Гейзенберг В. Физика и философия. Гл. 3. М., 1963. С. 31.

⁴ Эйнштейн А. и Инфельд Л. Эволюция физи­ки. Кванты света. С. 249.

необходимо представить себе фотон как частицу света, то тем не менее невозможно представить себе движения этой частицы в пространстве в соответствии с характер­ными для классической механики поняти­ями локализации в пространстве и траек-тории.

Ь) От классической механики к соотношению неопределенностей

В самом деле, объяснение с помощью фигур и движений по правилам классичес­кой механики предполагает знание поло­жения каждого из материальных элемен­тов, а также воздействующих на него сил. Такой тип объяснения хорошо представлен в небесной механике Ньютона, где сово­купность движений небесных тел объясня­ется на основе приложения сил притяжения к центру тяжести этих тел. Стремление распространить этот способ объяснения и предвидения выразилось в знаменитой формуле Лапласа:

Ум, которому были бы известны для ка­кого-либо данного момента все силы, оду­шевляющие природу, и относительное по­ложение всех ее составных частей, если бы вдобавок оказался достаточно обширным, чтобы подчинить эти данные анализу, об­нял бы в одной формуле движения вели­чайших тел вселенной наравне с движени­ями легчайших атомов: не осталось бы ничего, что было бы для него недостовер­но, и будущее, так же как и прошедшее, предстало бы перед его взором¹.

Эта формула постулирует возможность ис­черпывающего и абсолютно определенного знания универсума. Правда, она требует ума "достаточно обширного", чтобы под­вергнуть анализу бесконечное количество данных, то есть фактически бесконечного, или божественного, ума. Но знание, до­ступное такому уму, исключило бы всякую форму неопределенности или недостовер­ности.

Такая интерпретация отождествляет де­терминизм и достоверность и, следователь­но, исключает из сферы науки всякое толь-ко вероятное знание, даже когда эта вероят-

¹ Лаплас П. С. Опыт философии теории веро­ятностей. Гл. 1. М., 1908. С. 9.

ность принимает строго математическую форму исчисления вероятностей или стати­стического подсчета:

Признаюсь, я не понимаю, почему назы­вают законом результаты, получаемые из статистики; по-моему, научный закон мо­жет основываться лишь на абсолютной достоверности и абсолютном детерминиз­ме, но не на вероятности².

С этой точки зрения вероятность какого-либо физического явления вовсе не зависит от природы вещей, но "обусловливается отчасти... незнанием, а отчасти нашим зна­нием"³. Она обусловливается нашим знани­ем в том смысле, что вероятность, в от­личие от простой возможности, обнаружи­вает элемент детерминации, вытекающий из нашего знания реальности. Если мы говорим, например, что такая-то грань игральной кости имеет один шанс из шести выпасть при каждом броске, то это пото­му, что мы знаем, что у кости шесть граней и, насколько нам известно, она не поддель­ная. Но нам приходится удовлетворяться простой вероятностью (и в этом она обус­ловлена нашим незнанием), поскольку мы не можем определить все факторы, дейст­вующие при бросании кости (исходное по­ложение, направление и сила броска, угол падения, трение и т. д.). И лишь знание всех этих данных позволило бы нам оп­ределить результат с абсолютной досто­верностью.

Вероятность здесь рассматривается как существенно субъективная: она описывает не объективное состояние вещей, а только степень нашего знания (или незнания) реальности. Если ей и предоставляют какое-то место в науке, то лишь временно — до тех пор, пока прогресс науки не приведет к точному и достоверному оп­ределению.