Математический язык движения

Скорость – speed (rapidity of movement) и скорость – velocity (quickness, rate of motion) – термины, знакомые каждому, выросшему в XX веке. Два эти термина имеют четкие значения в точном научном языке, и они будут более подробно объяснены далее в Главе 3, но однако даже физики на них поскальзываются и используют их попеременно.

Скорость (speed) можно определить так:

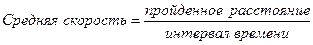. (1-1)

Характеристика «средняя» необходима для понимания того, что скорость может не быть одной и той же в любой части временного интервала. Выраженное более сжато в привычных символах, наше определение станет таким: 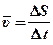. (1-1)

Здесь использована заглавная греческая буква дельта (Δ), чтобы обозначить изменение, или интервал, напоминая нам, что измерение сравнивает два разные положения для двух разных моментов времени. Конечно, мы могли бы использовать и однобуквенные символы для ΔS и Δt. Но обычный в научном языке прием служит, чтобы подтолкнуть память и передать более полно смысл формулы. Аналогично, черточка над υ является одним из нескольких привычных способов говорить о «средней величине» любого символа под чертой. Использование S как символа расстояния общепринято по некой туманной причине. Частично роль математики в науке состоит в расширении языка, а обозначение выбирается по соображениям ясности.

Если по формуле 1-1 рассчитать скорость вашей машины, скажем, за полчаса езды в городе, используя показания одометра и по вашим часам, вы могли бы получить величину 17 миль в час. Но за этой величиной могли бы скрываться 5 минут полной остановки в транспортной пробке и несколько минут смелой езды со скоростью 70 миль в час. Очевидно, множество деталей движения оказываются выпущенными. Чтобы сделать описание более полным, вы могли бы разделить вашу поездку на одноминутные интервалы, подсчитывая среднюю скорость на каждом интервале. Но когда же этот процесс нужно остановить?

Ответ физика прагматичен: когда я получу достаточное число деталей, чтобы ответить на заданный вопрос. Как грубое приближение к неприятной реальности автовождения в современном городе, ваше первое измерение скорости было достаточно хорошим. Но предположим, вы хотите получить данные, которые позволят вам сказать, насколько хороша ваша машина. Физик мог бы рассуждать так. При резком ускорении или торможении машина может изменять свою скорость на 10 миль/час за одну секунду. То есть если я выберу интервалы по 0,1 секунды, скорость в начале интервала будет отличаться от скорости в его конце не более чем на 1 милю/час. При интервалах в 1 миллисекунду (1мс = 0,001с= 1/1000с) я могу определить скорость с точностью 0,01 миль в час, и так далее.

Рисунок 1-1 позволяет графически проиллюстрировать проблему. Если объект движется с постоянной скоростью, то отношению пройденного

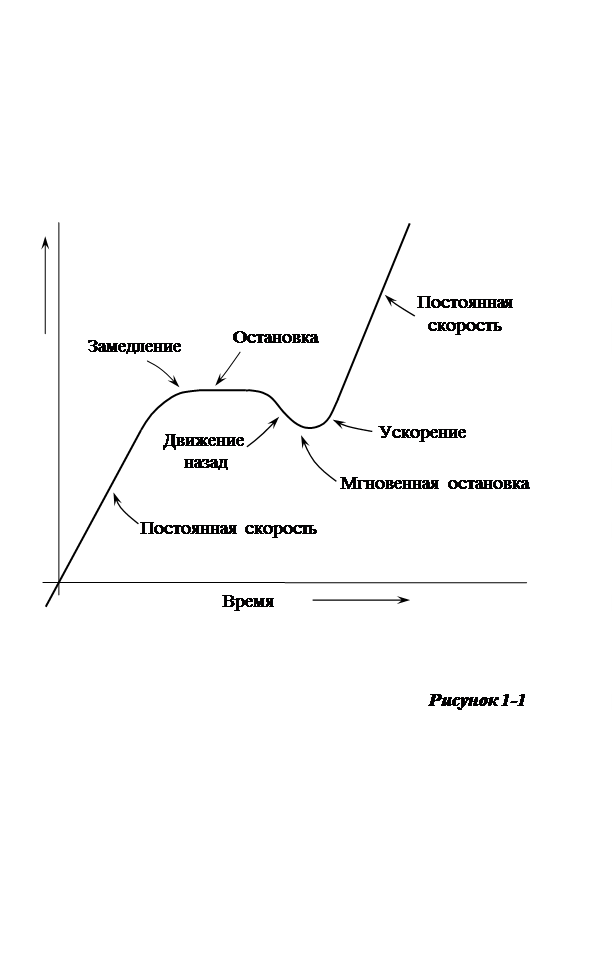
расстояния к прошедшему времени соответствует прямая линия. Чем круче эта линия, тем больше скорость. Крутизна графина называется его наклоном. Когда меняется скорость, изменяется и наклон. Таким образом, график расстояние-время для движения с переменной скоростью будет кривой линией.

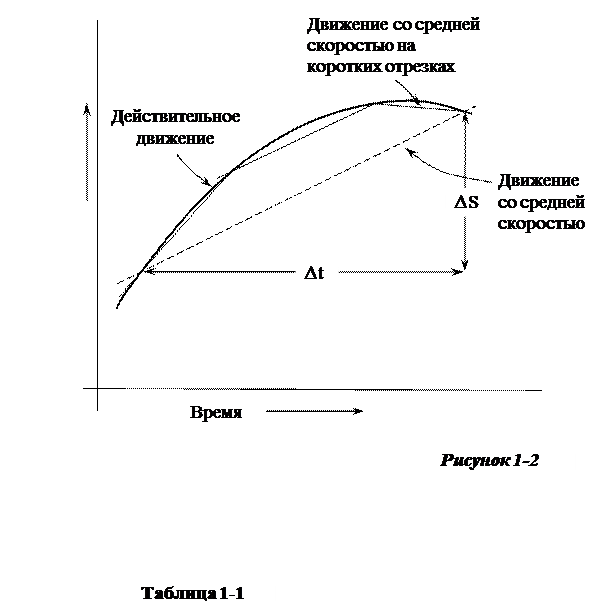
Когда скорость не постоянна, измерение средней скорости упускает многие детали графика. На рисунке 1-2 мы видим, что измерения на меньших интервалах более точно представляют действительное движение.

Конечно, для наилучшего описания потребовались бы бесконечно малые интервалы. В этом – смысл приведённых рассуждений, но нам нет нужды быть столь буквальными. Существо вопроса в том, что независимо от желаемой точности описания, её можно получить, просто выбирая интервал достаточно малым. Это убеждает нас в том, что можно говорить о скорости в конкретный момент. Спидометр автомобиля прямо измеряет эту скорость. При этом можем отбросить качественное прилагательное «средняя».

Нашим следующим шагом будет поиск способа, чтобы указать, как быстро меняется сама скорость. Ведь и автомобильные фирмы заявляют, что их изделие будет делать «от 0 до 60 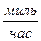за 6 секунд». Мы можем выразить нечто похожее таким же способом, каким мы определили скорость, назвав новую величину средним ускорением .

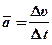По этому определению ускорение, заявленное в рекламе автомобиля, составит 10 миль в час за секунду. Физик содрогнется от использования часов в качестве единицы времени для скорости и секунд для ускорения и предпочтёт метры в сек за секунду для единицы ускорения, которая сократится до мс^-2. Как и при измерении скорости, Δυ вычисляется путём вычитания скорости в начале временного интервала из скорости в конце его.

Концепция ускорения трудна для понимания, так как является ступенчатой абстракцией, выделенной из прямого наблюдения некоторого объекта в конкретном месте в данный момент времени («здесь и сейчас»). Используя экономическую аналогию, можно сказать, что цена яиц в супермаркете – это конкретный факт. Утверждение, что скорость инфляции составляет 10 % в год, является абстракцией, такой же, какая использовалась при измерении скорости. Печальная новость, что ситуация ухудшается, т.к. скорость инфляции два месяца назад составляла только 8 % в год, является следующей ступенью абстракции, точно соответствующей понятию ускорения. Если мы разделим изменение скорости инфляции, которое равно 10–8=2 процента, на время между измерениями этой скорости (это 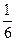года), мы получим «ускорение» цен 12% на год в квадрате, и аналогия будет полной.

Понятие ускорения одинаково хорошо подходит для процессов увеличения и уменьшения скорости. В последнем случае изменение скорости

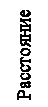
Время, с	Скорость, м/с	Путь падения, м
Средняя скорость = 30 м/с

(и, следовательно, ускорение) будет отрицательным. Таким образом, нам не нужна отдельная концепция замедления.

Важно твёрдо различать понятия скорости и ускорения, т.к. они могут быть полностью независимыми друг от друга и даже иметь разные знаки. Когда машина движется вперёд с возрастающей скоростью, и скорость и ускорение положительны. Если же машина движется вперёд с уменьшением скорости, то скорость положительна, но ускорение отрицательно. Для машины, которая едет назад с возрастанием скорости, и ускорение и скорость отрицательны. Но если машина замедляется, двигаясь назад, её скорость отрицательна, но ускорение положительно, т.к. скорость становится менее отрицательной, т.е. изменяется в положительном направлении!

Если это последнее предложение вам понятно, у вас очень хорошая голова для физики.

Возвращаясь к рисунку 1-1, становится ясно, что когда имеется ускорение, линия, описывающая движение, должна быть кривой. Если скорость объекта возрастает, график искривляется вверх, если скорость уменьшается, график искривляется вниз.

Решающий тест

Галилей использовал концепции, развитые выше, чтобы получить интересный результат, который можно сравнить с экспериментом и тем самым проверить теорию. Для равноускоренного движения тела, стартующего из состояния покоя, он получил соотношение между пройденным расстоянием и прошедшим временем. Его закон свободного падения тел на нашем новом языке движения есть не что иное как утверждение, что «а» является универсальной константой для падающих тел. То есть измеряя ускорение падающего тела, мы обнаружим его одним и тем же для всех времён во время падения и для всех падающих тел. Когда тело стартует из состояния покоя с постоянным «а», его средняя скорость до любого данного момента времени должна равняться половине скорости в этот самый конечный момент времени. В этом можно убедиться с помощью простых арифметических действий над числами во втором столбце таблицы 1-1. Числа в таблице соответствуют постоянному ускорению (равные изменения скорости за равные времена) 10 мс^-2, которое оказывается очень близким к ускорению свободно падающего тела. Этот результат можно выразить как 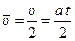,что означает: «Для нахождения средней скорости нужно умножить ускорение на время падения, чтобы получить конечную скорость, и разделить полученный результат на 2», т.к. тело ускорялось и поэтому в конце двигалось быстрее, чем во все более ранние времена. Чтобы получить расстояние, пройденное за время t, мы умножаем среднюю скорость на это время: 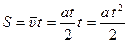. При интерпретации этой формулы, мы всегда должны помнить, что множитель 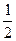следует из факта, что средняя скорость равна половине конечной скорости, а время входит в квадрате потому, что оно появляется дважды: оно позволяет телу ускориться, а также позволяет ему двигаться дальше со своей скоростью, какой бы она не была.

Чтобы продемонстрировать своё утверждение, что падающие тела получают одинаковое приращение скорости за равные времена (что равносильно демонстрации того, что пройденное расстояние изменяется как квадрат времени), Галилей встретился с серьёзными экспериментальными трудностями. Лучшими приборами своего времени он едва мог измерить интервалы времени с точностью до долей секунды. Однако тяжелый предмет, падающий с башни высотой 150 футов, коснётся земли уже через 3 секунды.

Чтобы решить проблему, Галилей начинает изучать скатывание шара по наклонной плоскости. С помощью остроумных аргументов он утверждал, что это «ослабляет» движение падающего тела (т.е. уменьшает ускорение) без изменения характера движения. Это утверждение должно быть принято на веру, потому что Галилей не имел законченной теории, чтобы показать, какой именно эффект даёт наклонная плоскость. Новая теория в физике редко бывает законченной при первой презентации; в ней часто имеются большие логические прорехи, которые должны быть заполнены позже.

Используя гладкую доску с малым наклоном и направляющую канавку для шара, Галилей смог создать на земле движение, длящееся около 10 секунд. Его таймер был груб, но адекватен своему времени: сосуд с водой и дыркой в днище, которую он затыкал своим пальцем. Когда палец вынимался, вода вытекала в чашку. Затем чашка тщательно взвешивалась. Количество воды в чашке было мерой времени. Результаты соответствовали предсказанию Галилея. Доказательство того, что результат имел отношение к проблеме свободного падения, было, конечно, некоторым логическим скачком. Но идеальные экспериментальные условия встречаются редко, и косвенные тесты, поддержанные аргументами, которые правдоподобны, но не достаточно строги, играют важную роль в развитии молодой науки.

Ошибался ли Аристотель?

Схоластам было бы легче спорить с Галилеем, если бы от них выступил человек, способный пользоваться стилем аргументов Галилея. Давайте исследуем вопрос свободного падения, став на время противником Галилея. Если бы мы действительно наблюдали падение тела с большой высоты, измеряли его скорость в каждый момент и представили результаты в виде графика, мы получили бы кривую, показанную на на рис. 1-3. Объяснение такого любопытного поведения очень просто. Т.к. тело ускоряется, сопротивление воздуха его движению возрастает. Наконец достигается скорость, при которой сила воздушного напора снизу вверх уравновешивает 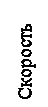силу притяжения тела к земле, и ускорение становится равным нулю. Такая скорость называется предельной (терминальной) скоростью объекта. Довольно интересно сравнить падение тел одинакового размера и формы. Их терминальные скорости окажутся практически пропорциональными их весам, как в законе свободного падения Аристотеля. Тяжелому стальному шару, падающему с самолёта, могут потребоваться тысячи футов, чтобы достичь терминальной скорости, а человеческое тело достигнет её уже после нескольких сотен футов падения, – в этом секрет парения в воздухе, которое соответствует долгому падению с терминальной скоростью, вслед за которым раскрывается парашют, чтобы снизить терминальную скорость для благополучного (безопасного) приземления.

Гораздо проще изучить движение тела с низкой терминальной скоростью, например, легкого объекта, падающего в плотной среде, скажем, мяча для гольфа в воде. Объекты такого рода Аристотель обсуждал особенно часто. Нельзя a priori считать такой приём замедления падения менее законным, чем выбор наклонной плоскости Галилеем. В плотной среде объект может достичь терминальной скорости за доли секунды.

График зависимости скорости от времени может выглядеть как кривая на рис. 1-4.

Графики будут ещё более впечатляющими, когда мы учтём, что реальными измерениями, по необходимости, должны быть расстояние и время. Реальный эксперимент, выполненный с инструментами галилеевского времени, дал бы результаты, представленные на рисунке 1-5 в графической форме, как это принято в научных журналах. По этим данным любой разумный аналитик мог заключить, что Аристотель был ближе к истине, чем Галилей. Всё, что мы должны сделать, – это допустить, что процесс достижения терминальной скорости не является мгновенным, и Аристотель освобождается от трудностей с помощью незначительной модификации первоначальной гипотезы. Если добавить к этому представление античной философии о том, что среда, в действительности, является источником движущей силы при падении тела, а вакуум, который Галилей рассматривал в качестве своей идеальной ситуации, является самым неестественным состоянием, то мы могли бы логично заключить, что Аристотель рассмотрел более фундаментальную ситуацию, в то время как Галилей был сбит с пути своим чрезмерным интересом к мимолётным явлениям, которые исчезают, если мы наблюдаем достаточно долго.

«Конечно», – мы могли бы сказать Галилею, – «Вы позволили ввести себя в заблуждение тем фактом, что тяжелым объектам, падающим в воздухе, по каким-то причинам, требуется большое время, чтобы достичь своей терминальной скорости. Кроме того, свои экспериментальные данные вы получили на наклонной плоскости, которая может и не иметь отношения к проблеме свободного падения».

Но оказывается, эта вполне резонная точка зрения является ошибочной: не потому, что она хуже соответствует природе, просто закономерности, которые наблюдал Аристотель, оказывается, имеют гораздо меньшее 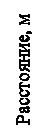фундаментальное значение, чем те, что наблюдал Галилей, особенно, если рассматривать их в контексте последующего развития науки механики.

На самом деле, Галилей описал и эксперименты с падающими телами в жидкостях и понял, что работа Аристотеля имеет определенную ценность. Однако Галилей был достаточно тщеславен, чтобы атаковать Аристотеля по незначительному поводу, например, за то, что тот не учёл разницу в весе между погруженным объектом и тем же объектом на воздухе. Этот эффект был открыт Архимедом уже после жизни Аристотеля. С такой коррекцией предсказания Аристотеля выполнялись бы ещё лучше, но Галилей с его инстинктом спорщика, настаивал на том, чтобы современные ему последователи Аристотеля придерживались первоначальной (исходной) версии теории, а сами они были слишком ограниченны, чтобы усилить свою позицию, осовременив теорию Аристотеля.

Галилей пришел к выводу, что движение тел, падающих в жидкостях, зависит от слишком большого числа факторов, таких как форма и размер тела, и зависит от них так же сильно, как и от веса, чтобы представлять собой важный фундаментальный закон природы. Он нашёл свою собственную закономерность: универсальную скорость и постоянное ускорение свободного падения, – вещи гораздо более привлекательные в качестве закона природы. Последующее развитие науки подтвердило его интуицию. Этот закон Галилея представляет собой нечто большее, чем просто наблюдение, и показывает, что хвалёная объективность науки не так проста, как кажется на первый взгляд.

Урок, который должен быть извлечен из этого упражнения в такой «адвокатской» защите Галилея методом «от противного», с позиций его оппонентов, состоит в том, что нет ничего автоматического в научном процессе. Предположим на минуту, что эта конкретная проблема была бы самой актуальной на фронте научных исследований сегодня. Хорошо подготовленный физик, доктор наук, мог бы получить большой грант на изучение падающих тел. Средства он мог бы использовать для получения большого массива данных по падающим объектам со всевозможными комбинациями веса, формы, размера, среды и т.п. Он и его ученики добивались бы улучшения и умножения своих измерений, «выдавая» поток статей для научных журналов. Вполне вероятно, что встретившись с необходимостью объяснить все эти данные с разумной точностью, но без законченной теории, они двинулись бы в направлении точки зрения Аристотеля, и полностью проглядели бы прозрение Галилея. Наука – это больше, чем просто попытка описать природу с максимально возможной точностью. Часто истина глубоко спрятана, и закон, который даёт плохое приближение к природе, имеет бóльшее значение, чем закон хорошо работающий, но отравленный в самом корне (неверный в основе).