Геометрическое сложение четырех и более векторов
Правило геометрического сложения векторов можно распространить на сумму множества заданных векторов.
Правило.Сумму векторов можно получить следующим образом. Из произвольной точки  откладывается вектор, равный первому слагаемому вектору. К концу первого вектора присоединяется начало второго вектора; к концу второго – начало третьего. Вектор, соединяющий начало первого вектора с концом последнего, является суммой данных векторов. откладывается вектор, равный первому слагаемому вектору. К концу первого вектора присоединяется начало второго вектора; к концу второго – начало третьего. Вектор, соединяющий начало первого вектора с концом последнего, является суммой данных векторов. |
Чтобы задать вектор, нужно задать его модуль и направление. Направление вектора определяется его линией действия. Поэтому в задачах на сложение векторов удобно пользоваться линиями действия векторов, на которых удобно откладывать модули заданных векторов.
Определение.Суммой несколько векторов 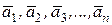 (рис. 9.14, а) называют вектор
(рис. 9.14, а) называют вектор
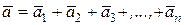 .
.
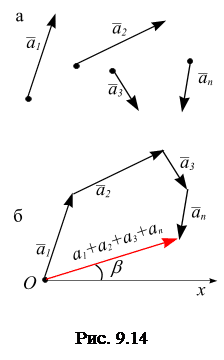
Геометрическое правило сложения нескольких векторов основано на построении векторного многоугольника (по подобию построения векторного треугольника). Возьмем произвольную точку О и путем параллельного переноса совместим начало вектора 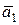 с этой точкой. Далее последовательно путем параллельного переноса пристраиваем другие векторы один за другим так, чтобы начало последующего вектора совпадало с концом предыдущего, тогда вектор, замыкающий получившуюся ломаную, является суммой слагаемых векторов, причём, его начало совпадает с точкой А (началом первого из слагаемых векторов), а конец – с концом последнего вектора (рис. 9.14, б).
с этой точкой. Далее последовательно путем параллельного переноса пристраиваем другие векторы один за другим так, чтобы начало последующего вектора совпадало с концом предыдущего, тогда вектор, замыкающий получившуюся ломаную, является суммой слагаемых векторов, причём, его начало совпадает с точкой А (началом первого из слагаемых векторов), а конец – с концом последнего вектора (рис. 9.14, б).
Геометрическая сумма векторов
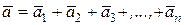
определена вектором, соединяющим точку О (начало вектора 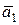 ) с концом последнего вектора
) с концом последнего вектора 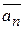 . Если построения векторов делать в масштабе, то, измеряя длину полученного вектора
. Если построения векторов делать в масштабе, то, измеряя длину полученного вектора  , получим его модуль, измеряя транспортиром угол
, получим его модуль, измеряя транспортиром угол  , который образует вектор
, который образует вектор  с положительным направлением оси
с положительным направлением оси 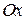 , определим направление вектора
, определим направление вектора  .
.
Пример 9.9.Вычислить сумму трех векторов  ,
,  ,
, 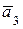 ,
, 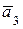 , если
, если 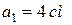 ,
, 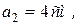
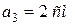 ,
, 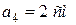 . Направления векторов показаны на рис. 9.15.
. Направления векторов показаны на рис. 9.15.
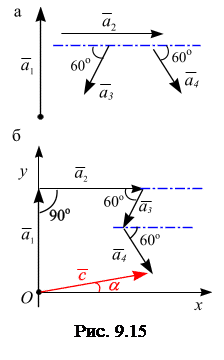 Решение. Совместим ось
Решение. Совместим ось 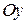 декартовой системы координат
декартовой системы координат 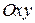 с линией действия вектора
с линией действия вектора  , а начало – с точкой приложения вектора
, а начало – с точкой приложения вектора  (рис. 9.15, в). Откладываем отрезок вдоль оси
(рис. 9.15, в). Откладываем отрезок вдоль оси 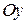 , равный модулю первого вектора–
, равный модулю первого вектора– 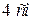 . Далее, через конец вектора
. Далее, через конец вектора  проводим прямую, параллельную линии действия вектора
проводим прямую, параллельную линии действия вектора  (угол между линиями действия векторов
(угол между линиями действия векторов  и
и  равен
равен 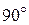 ), и откладываем отрезок, равный модулю второго вектора –
), и откладываем отрезок, равный модулю второго вектора – 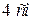 ; через конец вектора
; через конец вектора  проводим прямую, параллельную линии действия вектора
проводим прямую, параллельную линии действия вектора 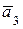 (угол между линиями действия векторов
(угол между линиями действия векторов  и
и 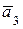 равен
равен 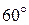 ), и откладываем отрезок, равный модулю третьей силы –
), и откладываем отрезок, равный модулю третьей силы – 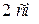 . Через конец вектора
. Через конец вектора 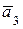 проводим прямую, параллельную линии действия вектора
проводим прямую, параллельную линии действия вектора 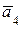 (угол между линией действия вектора
(угол между линией действия вектора 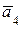 и положительным направлением оси
и положительным направлением оси 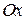 равен
равен 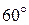 ), и откладываем отрезок, равный модулю четвертой силы –
), и откладываем отрезок, равный модулю четвертой силы – 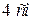 . Вектор
. Вектор 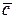 , равный сумме векторов
, равный сумме векторов 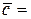
 +
+  +
+ 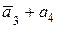 , соединяет точку О (точка приложения первого вектора) с концом вектора
, соединяет точку О (точка приложения первого вектора) с концом вектора 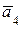 (рис. 9.15, б). Измеряем линейкой модуль вектора
(рис. 9.15, б). Измеряем линейкой модуль вектора 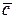 :
: 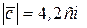 .
.
Измерим транспортиром угол между положительным направлением оси 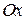 и вектором
и вектором 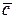 :
: 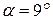 .
.
В результате измерений получили характеристики вектора
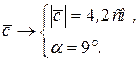
Разность векторов
Разностью двух векторов  и
и 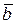 называется третий вектор
называется третий вектор 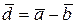 , сумма которого с вычитаемым вектором
, сумма которого с вычитаемым вектором 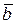 дает вектор
дает вектор  . Таким образом, если
. Таким образом, если 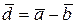 , то
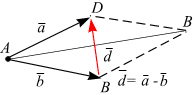
, то 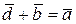 (на рис. 9.16 а). Вектор
(на рис. 9.16 а). Вектор 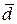 соответствует малой диагонали BD параллелограмма, построенного на векторах
соответствует малой диагонали BD параллелограмма, построенного на векторах  и
и 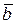 , как на сторонах:
, как на сторонах:
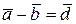 .
.
 а а | 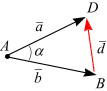 б б |
Рис. 9.16
Модуль вектора d вычисляется по теореме косинусов, рис. 9.16:
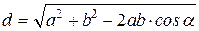 .
.
Следует обратить внимание на направление вектора 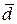
(рис. 9, 16, б): вектор 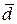 направлен от конца вектора
направлен от конца вектора 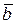 (точка B) к концу вектора
(точка B) к концу вектора  (точка D).
(точка D).
