Предыстория появления логических машин

Первые попытки создать такие механические устройства, которое бы производили простейшие арифметические операции, уходят в далекую древность. Из дошедших до наших дней литературных источников известно, что древние греки, напр., сконструировали механические приспособления для решения некоторых задач.

Р.Луллий (ок.1235 – 1315) – испанский философ – идеалист и логик, богослов, писатель. В тридцать лет решил стать миссионером, отказавшись от благ придворной жизни. Логику Р.Луллий именовал «великим искусством» распознавать при помощи разума истину и ложь и отделять их друг от друга.

В средние века, как известно, Раймунд Луллий попытался осуществить с помощью механического устройства идею механического комбинирования понятий. Его «логическая машина» состояла из семи вращающихся вокруг центра кругов. На каждом из них были написаны слова, обозначающие различные понятия (например, «человек», «знание», «количество» и т. п.) и логические операции (например, «равенство», «противоречие» и т. п.). Вращая эти круги, можно было создавать всевозможные сочетания понятий. С помощью такой «машины» Луллий получал силлогического типа выводы из заданных посылок.

При жизни Р.Луллия его идея была встречена с недоверием. Но уже в XVII в. Луллевское предложение о механизации умозаключения, умственных процессов оказало большое влияние на основоположника математической логики немецкого философа Г.В. Лейбница (1646 - 1716). В XIX в. идею логической машины пытался осуществить английский логик У. Джевонс (1835 - 1882).

Р.Луллию приписывают около 300 сочинений, часть которых посвящена проблемам логики. Он исследовал силлогизм, индукцию, правила следования, логические связки «и» и «или» [12].

Силлогизм (греч. syllogismos — сосчитывание) — умозаключение, в котором из двух категорических суждений, связанных общим средним термином, получается третье суждение, называемое выводом; при этом средний термин в заключение не выходит.

Аристотель определил силлогизм как высказывание, в котором «при утверждении чего-либо из него необходимо вытекает нечто отличное от утверждаемого и именно в силу того, что это есть» [1].

Силлогизм — это умозаключение, в силу которого, признав истинность посылок силлогизма, нельзя не согласиться с истинностью заключения, вытекающего из посылок. Напр.:

Все граждане России имеют право на труд;

Федоров — гражданин России;

Федоров имеет право на труд.

Если исходные суждения силлогизма истинны, то, при условии соблюдения соответствующих правил силлогизма, в результате умозаключения получается истинный вывод, как это и имеет место в только что приведенном примере.

Силлогизм состоит из трех суждений. Это опосредствованное умозаключение. В первом суждении содержится общее правило («Все граждане России имеют право на труд»). Во втором суждении приводится конкретный случай («Федоров является гражданином России»). И, наконец, в третьем суждении дается вывод, или заключение («Федоров имеет право на труд»).

Каждое из этих суждений имеет свое собственное название. Суждение, в котором содержится общее правило, называется большей посылкой; суждение, в котором дается частный случай,— меньшей посылкой; а третье суждение, в котором приводится вывод из посылок,— заключением силлогизма. Для удобства изучения силлогизма в учебниках логики принято располагать все три суждения, входящие в силлогизм, одно под другим в виде колонки. При этом заключение отделяется от посылок горизонтальной чертой.

В этом свете современные логики одну из великих заслуг Аристотеля видят в том, что он впервые в истории науки не только подверг анализу с некоторой формальной точки зрения приемы рассуждения, которые практически широко применялись его современниками, но и систематизировал их и открыл объективные правила, которые распространяются на частные случаи и которые независимы от частных конкретных объектов.

Введя буквенные символы для обозначения переменных, Аристотель заложил основы формального построения логики. «Введение в логику переменных,— замечает известный польский логик Я. Лукасевич,— является одним из величайших открытий Аристотеля». Ведь буквы — это знаки общности, которые свидетельствуют, что заключение при соблюдении правил будет следовать из посылок всегда, какой бы конкретный термин мы ни избрали вместо букв.

Вообще трудно переоценить те перспективы, которые открыло перед логикой и наукой в целом введение Аристотелем переменных. Так, переменная А, которой можно обозначить общеутвердительное суждение, входящее в силлогизм, отобразила бесконечное множество конкретных суждений, в которых зафиксировано наше знание о том, что каждому предмету какого-либо класса (множества) присуще одно или несколько определенных свойств. Оперирование переменными, говорит Д. П. Горский, освобождало науку от введения и определения огромного (практически бесконечного) количества собственных имен. Вместе с переменной в науку вошел особый тип определений — контекстуальных определений. Вместо того, чтобы определять явно (через таблицы, например) каждое значение функции, мы можем ее записать в виде одного выражения, заключающего все множество ее значений. Переменные явились основой для возникновения и совершенствования научных идеографическо-символических языков, в том числе и для формализованных языков, играющих столь большую роль в развитии современной кибернетической техники.

Переменные Аристотель связывал в посылках с помощью четырех логических постоянных (констант — см.): «быть присуще всем» и «не быть присуще ни одному», «быть присуще некоторым» и «не быть присуще некоторым». Затем, в зависимости от того, какими логическими константами связываются попарно термины в посылках и каково положение общего термина, связывающего крайние термины, Аристотель установил три фигуры и соответствующее каждой фигуре число модусов силлогизма.

Силлогистика Аристотеля, заключает Лукасевич, «является системой, точность которой превосходит даже точность математической теории, и в этом ее непреходящее значение. Но это узкая система, не применимая ко всем видам рассуждений, например к математическим доказательствам. Возможно, Аристотель сам чувствовал, что его система не была пригодна для всякой задачи, так как он позднее к теории ассерторических силлогизмов добавил теорию модальных силлогизмов. Это было, конечно, расширением логики, но, по- видимому, не в надлежащем направлении. Логика стоиков — изобретателей античной формы пропозиционального исчисления — имела гораздо более важное значение, чем все силлогизмы Аристотеля. В настоящее время мы понимаем, что теория дедукции и теория кванторов являются фундаментальными Отраслями логики».

Силлогистика, как справедливо пишет А. Л. Субботин, «была той исторически первой логической системой, описание и исследование которой положило начало формальному рассмотрению логики и тем самым формальной логике как науке». Г Н. Поваров замечает, что традиционная теория категорического силлогизма была математико-логической теорией, только ее математическим аппаратом была не алгебра, а комбинаторика.

В первой половине XVII в. французский математик и логик Блез Паскаль (1623—1662) сконструировал машину для выполнения арифметических операций.

Паскаль Блез (1623—1662) — французский математик, философ и логик, приверженец декартовской дедуктивной системы, один из родоначальников современного аксиоматического метода и теории вероятностей. Им сформулирован и практически использован метод полной математической индукции. В 1642 г. Паскаль сконструировал первую вычислительную машину для операции сложения, которая имела два типа органов:

1)органы установления связи между машиной и оператором (записыватель и визир с оконцем, в котором появлялась цифра) и

2) органы, производящие операции. Чертеж механизма этой машины приведен в на рис 2.1

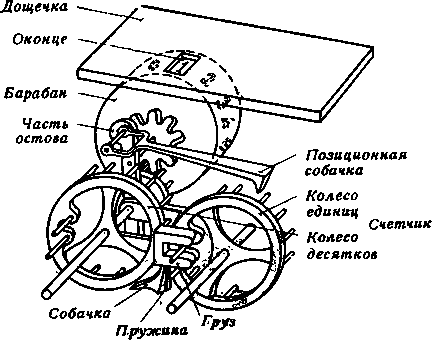
Рис 2.1. Машина Паскаля