Фігури категоричного силогізму, правила фігур

Фігури категоричного силогізму:

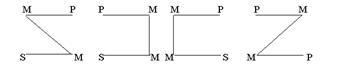
Фігури силогізму – це його різновиди, які розрізняються місцем середнього терміна в засновках.

Модусом простого категоричного силогізму є різновиди силогізмів, які різняться кількістю і якістю засновків.

1 фігура: ААА, ЕАЕ, АІІ, ЕІО.

2 фігура: ЕАЕ, АЕЕ, ЕІО, АОО,

3 фігура: ААІ, ІАІ, АІІ, ЕАО, ОАО, ЕІО.

4 фігура: ААІ, АЕЕ, ІАІ, ЕАО, ЕІО.

Правила 1-ї фігури: 1. Більший засновок – загальне судження.

2. Менший – ствердне судження.

1 фігура – найбільш типова форма дедуктивного умовиводу.

Правила 2-ї фігури: 1. Більший засновок – загальне судження.

2. Один із засновків – заперечне судження.

Правила 3-ї фігури: 1. Менший – ствердне.

2. Висновок – часткове судження.

Правила 4-ї фігури не розглядаються, бо вони не ти пічні для мислення – звича йно це виводи 1 фігури.

Полісилогізми

Полісилогізмом називаються два або декілька простих категоричних силогізмів, пов”язаних один з одним так, що висновок одного є засновком для іншого:

1.Прогресивний полісилогізм-висновок попереднього силогізму стає більшим засновком наступного силогізму.

Прогресивний сорит можна отримати з прогрествного полісилогізму шляхом послідовного вилучення висновків передуючих силогізмів і більших наступних засновків.

2.Регресивний полісилогізм-висновок передуючого силогізму стає меншим засновком наступного силогізму

Регресивний сорит можна отримати з регресивного полісилогізму шляхом послідовного вилучення висновків передуючих силогізмів і менших засновків, що випливають з них.

Індуктивні умовиводи

Умовивід – це форми мислення, у якій з одного чи кількох істинних суджень на основі певних правил виводи виводять нове судження. Структура: засновок, висновок, логічний зв’язок між засновками та висновками. Умовивід буде правильним, якщо в ньому виконуються основні закони логіки.

Індуктивний умовиводи – це опосередковані умовиводи у яких з одиничних суджень – засновків – виводять часткое або й загальне судження – висновок.

А)повна індукція – різновид індуктивного умовиводу, в якому на підставі знання про належність певної ознак кожному предметові класу робиться висновок про належність цієї ознаки всім предметам цього класу. Наприклад: Прямокутні трикутники мають площу, що дорівнює половині добутку (множенню) основи на висоту. Тупокутні трикутники мають площу, яка дорівнює половині добутку основи на висоту. Гострокутні трикутники мають площу, яка дорівнює половині добутку основи на висоту. Значить всі трикутники мають площу, яка дорівнює половині добутку основи на висоту.

Б)неповна індукція - індуктивний умовивід, в якому висновок про весь клас предметів робиться на підставі знання тільки деяких предметів цього класу.

Аналогія, її різновиди

Аналогія – традуктивний умовивід, в якому на підставі подібності двох предметів в одних ознаках робиться висновок про подібність їх в інших ознаках.

Прикладом аналогії може бути міркування Галілея, який, відкривши чотири супутники Юпітера і виявивши спільність між системою „Юпітер – його супутники” і сонячною системою, зробив висновок, згідно з яким подібно до того, як у системі Юпітера в центрі перебуває найбільше за розмірами тіло, так і в центрі руху планет перебуває найбільше за об’ємом тіло цієї системи – Сонце.

Схема міркування за аналогією: Предмет А має ознаки abcd. Предмет В має ознаки abc. Ймовірно, що предмет В має ознаку d.

Висновок за аналогією має ймовірний характер.

Оскільки предмети можуть уподібнюватися один одному за своїми ознаками (властивостями), так і відношеннями між ними, то аналогії, відповідно, поділяються на аналогії властивостей і аналогії відношень. Міркування Галілея є прикладом аналогії відношення. Міркування, що на Марсі існує життя – приклад аналогії властивостей.

Хоча ймовірність висновків за аналогією загалом нижча, ніж за неповною індукцією, проте її евристичну роль важко перебільшити. Аналогія в історії нерідко була формою винятково сміливих гіпотез, обґрунтування яких призводило до епохальних відкриттів.

Проста аналогія – аналогія, в якій на підставі подібності предметів за одними якими-небудь ознаками роблять висновок про їх подібність в інших ознаках.

Строга аналогія – аналогія, що ґрунтується на знанні залежності ознак предметів, які порівнюються.

Нестрога аналогія – аналогія, в результаті якої робиться висновок від подібності двох предметів в одних ознаках до подібності ї за такою ознакою, про зв’язок якої з першими нічого не відомо.