Вписанные и описанные около треугольника окружности. Вневписанная окружность

Окружность называется вписанной в треугольник, если все стороны треугольника являются касательными к окружности. В этом случае радиусы, проведенные в точки касания являются перпендикулярами к сторонам треугольника

Окружность называется описанной около треугольника, если она проходит через все его вершины.

ТЕОРЕМА Через три точки, не лежащие на прямой, можно провести окружность и притом только одну, иначе говоря: около любого треугольника можно описать окружность. Центром этой окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.

ЗАМЕЧАНИЕ: В остроугольном треугольнике центр описанной окружности лежит внутри треугольника, в тупоугольном - вне треугольника, в прямоугольном треугольнике центр лежит на середине гипотенузы, а радиус равен половине гипотенузы.

ТЕОРЕМА Во всякий треугольник можно вписать окружность и притом только одну. Центром этой окружности является точка пересечения биссектрис углов треугольника, а радиусом - перпендикуляр, опущенный из центра на сторону.

ТЕОРЕМА В прямоугольном треугольнике радиус вписанного круга равен разности полупериметра треугольника и гипотенузы.

Окружность называется вневписанной для треугольника, если она касается одной из сторон треугольника и продолжения двух других.

Если стороны треугольника равны , то справедливы следующие формулы для нахождения площади треугольника

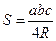,где R- радиус описанной окружности.

, где 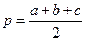-полупериметр, а r- радиус вписанной окружности

Задания с решениями

1. Найдите радиус окружности, описанной около прямоугольного треугольника ABC, если стороны квадратных клеток равны 1.

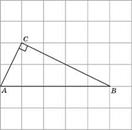
Решение

Так как треугольник прямоугольный, то центром описанной окружности является середина гипотенузы. Гипотенуза АВ=5, следовательно, R=2,5

Ответ 2,5

2. В прямоугольном треугольнике катеты 5 см и 12 см.Найти площадь

вписанного круга.

Решение

По условию АС=5, ВС=12 .По теореме Пифагора найдем длину гипотенузы АВ
.

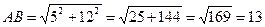Площадь треугольника АВС найдем двумя способами.

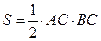и , где 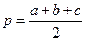-полупериметр, а r- радиус вписанной окружности.

Тогда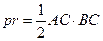

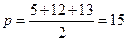
Получаем уравнение

Площадь вписанного круга найдем по формуле

Ответ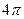

3.Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу c этого треугольника. В ответе укажите .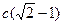

Решение

Обозначим равные катета треугольника .Тогда по теореме Пифагора получим уравнение Откуда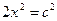

Площадь треугольника АВС найдем двумя способами.

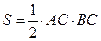и , где 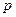-полупериметр, а r- радиус вписанной окружности.

Тогда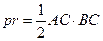

Получаем 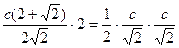Откуда получаем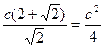

Тогда 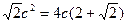и

В ответ надо записать 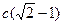, то есть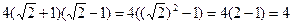

Ответ 4

4. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Решение

АС=ВС=СК+КВ=5+3=8

По свойству касательных, проведенных к окружности из одной точки DB=BK=3

О- центр вписанной окружности, поэтому он лежит на биссектрисе угла С, но так как треугольник равнобедренный то эта биссектриса является и медианой и высотой. Тогда AD=DB=3 Тогда АВ=6

Тогда периметр

Ответ 22

5. В равнобедренном треугольнике боковая сторона делится точкой касания со вписанной окружностью в отношении 8:5, считая от вершины, лежащей против основания. Найти основание треугольника, если радиус вписанной окружности равен 10.
Решение

По условию СК:КВ=8:5, значит СК=8х, КВ=5х.

Тогда СВ= 13х, и по свойству касательных, проведенных к окружности из одной точки, DB=КВ=5х, АВ=10х

Из треугольника DCB по теореме Пифагора найдем СD.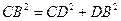

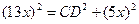
Площадь треугольника АВС найдем двумя способами.

и , где p -полупериметр, а r- радиус вписанной окружности.

Тогда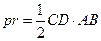

По условию r=10.

Получаем уравнение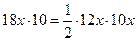

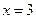Тогда АВ=30

Ответ 30

6.Стороны треугольника равны 25,24 и 7..Найти длину окружности, описанной около треугольника и площадь круга, вписанного в треугольник.

Решение

Найдем площадь треугольника по формуле Герона

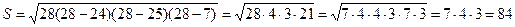
Для нахождения площади треугольника справедливы формулы 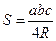,где R- радиус описанной окружности.

, где 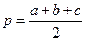-полупериметр, а r- радиус вписанной окружности

Подставив в эти формулы числовые значения площади и длин сторон получим уравнения и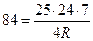

Тогда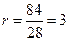

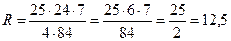
Длина описанной окружности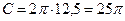

Площадь вписанного круга

Ответ 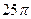и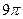

7. Расстояния от вершин треугольника до точек касания вписанной в этот треугольник окружности равны соответственно 2, 6 и 4. Найти длину вписанной окружности и площадь круга, описанного около этого треугольника этого треугольника.

Решение

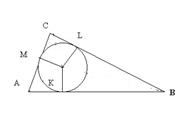
Касательные проведенные к окружности из одной точки равны между собой, поэтому MC=CL=2, AM=AK=4, BK=BL=6.

Тогда AC=2+4=6, AB=4+6=10, BC=2+6=8.

Так как 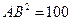и 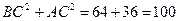, то треугольник АВС прямоугольный.

Гипотенуза АВ=10, следовательно, R=5 и следовательно площадь круга, описанного около треугольника равна .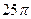

Площадь треугольника найдем двумя способами.

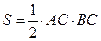и , где 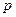-полупериметр, а r- радиус вписанной окружности.

Тогда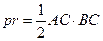

Получаем уравнение

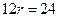
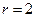Тогда длина вписанной окружности равна 4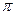

Ответ 4 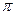и 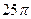.