Исходными данными для структурного этапа являются:
1. абстрактный автомат, заданный в виде графа или таблицы переходов и выхода;
2. система логических элементов, на которых необходимо реализовать автомат;
3. тип элемента памяти, который используется в автомате;
4. требования к схеме автомата по сложности и быстродействию.
Результатом этапа является функциональная схема автомата из заданных логических элементов.
На структурном этапе автомат рассматривается в виде следующей схемы (рис. 4.1) где:
КС – комбинационная схема, реализующая функции возбуждения элементов памяти и функции выходов структурного автомата;
БП – блок памяти для хранения кода текущего состояния автомата;
ЭП – элемент памяти для хранения одного разряда кода состояния.
![]()
Рис. 4.1
1. x1, x2, … xn – входные переменные структурного автомата, которые обозначают кода символов входного алфавита;
2. z1, z2, … zm – выходные переменные структурного автомата, которые обозначают разряды кода символов выходного алфавита;
3. y1, y2, … yk – внутренние переменные структурного автомата, которые обозначают разряд кода символов состояний;
4. y’1, y’2, … y’k – функции возбуждения элементов памяти структурного автомата.
Между объектами абстрактного и структурного автоматов существует следующее однозначное соответствие (табл. 4.1).
Таблица 4.1
| Абстрактный автомат | Структурный автомат |
| P = {p1, p2, …,pn} |  = {α1, α2, …, αn} = {α1, α2, …, αn} |
| W = {w1, w2, …,wm} |  = {β1, β2,…, βm} = {β1, β2,…, βm} |
| S = {s1, s2, …,sq} |  = {γ1, γ2,…, γq} = {γ1, γ2,…, γq} |
| sj = φ(si,pk) | y’1 = φ’ 1 (  , ,  ) … y’q = φ’q ( ) … y’q = φ’q (  , ,  ) ) |
| функция выхода автомата Мура: wj = ψ(sj) | z1 = ψ’ (  ) … zm = ψm’ ( ) … zm = ψm’ (  ) ) |
| функция выхода автомата Мили: wj = ψ(sj , pk) | z1 = ψ1’ (  , ,  ) … zm = ψm’ ( ) … zm = ψm’ (  , ,  ) ) |
αi , βj , δk – двоичные наборы, являющиеся кодами символов, соответствующих алфавитов.
 ,
,  – множества двоичных наборов соответствующие алфавитам абстрактного автомата.
– множества двоичных наборов соответствующие алфавитам абстрактного автомата.
y’1, …, y’q – булевы функции возбуждения элементов памяти, реализующие функции переходов абстрактного автомата.
z1 ,…, zm – булевы функции выходов структурного автомата, реализующие функции выхода абстрактного автомата.
Переход от абстрактного автомата к структурному автомату обусловлен двоичной структурой электрических логических элементов, из которых он будет реализован.
Основные этапы структурного синтеза:
1. кодирование символов входного и выходного алфавитов;
2. кодирование состояний абстрактного автомата;
3. после замены символов абстрактного автомата в исходной таблице переходов и выхода на их коды получается кодированная таблица переходов и выходов, которая описывает уже структурный автомат;
4. на основе полученной кодированной таблицы строится система булевых функции возбуждения элементов памяти и выходов автомата;
5. совместная минимизация полученной системы булевых функций;
6. реализация минимальной системы булевых функций из заданных логических элементов.
7. построение блока памяти ;
8. построение функциональной схемы всего автомата.
4.1. Типы элементов памяти
. В качестве элементов памяти структурного автомат используется двоичный элемент – триггер, который может находиться в одном из двух устойчивых состояний "1" или "0".
Элементом памяти будем называть автомат Мура, обладающий полной системой переходов и выходов.
Автомат обладает полной системой переходов, если любой пары состояний si и sj можно указать сигнал, вызывающий переход из si в sj.
Автомат обладает полной системой выходов, если каждому состоянию автомата можно приписать выходной сигнал, отличный от выходных сигналов других состояний.
Триггер обычно имеет два выхода: прямой и инверсный.
Состояние триггера определяется значением на его прямом выходе.
Основные типы триггеров.
Существует четыре основных логических типов триггеров:
два одновходовых: D –триггер и T -триггер;
два двухвходовых: RS –триггер и JK-триггер.
D - триггер или триггер - задержка (delay).
На выходе триггера повторяется значение на его входе
Граф автомат Мура, задающий D – триггер (рис. 4.2). Дуги графа помечены значениями входа D.
Таблица 4.2
Рис. 4.2
При задании триггера графом автомата Мура обозначение выхода q совпадает с обозначением состояния автомата и имеют тоже значение, поэтому таблица переходов триггера не содержит выходной символ (табл. 4.2).
| q(t) →q(t+1) | D |
| 0 → 0 | |
| 0 → 1 | |
| 1 → 0 | |
| 1 → 1 | |
Рис. 4.3
Рис. 4.4
Другим способом задания работы триггера является матрица переходов (рис. 4.3), где: q(t) – состояние триггера в текущем такте; q(t+1) – в следующем при подаче на вход соответствующего значения D.
На рис. 4.4 приведено условное обозначение D – триггера.
T- триггер или счетный триггер (тoggle - кувыркаться).
При подаче на вход единицы триггер меняет свое состояние на противоположное.
Граф автомат Мура, задающий T – триггер (рис. 4.5). Дуги графа помечены значениями входа T. Таблица переходов - (табл. 4.3).
Таблица 4.3
Рис. 4.5
Матрица переходов T – триггера приведена на рис. 4.6, а условное обозначение на рис. 4.7.
| q(t) →q(t+1) | T |
| 0 → 0 | |
| 0 → 1 | |
| 1 → 0 | |
| 1 → 1 | |
Рис. 4.6
Рис. 4.7
RS – триггер.
S – вход установки «1» (set), т.е. при подаче «1» на вход S, триггер переходит в состояние «1» (установка 1).
R – вход установки «0» (reset), т.е. при подаче «1» на вход R, триггер переходит в состояние «0» (сброс в 0).
Подача на входы S и R двух единиц одновременно запрещена.
Подача на входы S и R двух нулей одновременно не меняет состояние триггера.
Граф автомат Мура, задающий RS – триггер (рис. 4.8). Дуги графа помечены значениями входов S R. Таблица переходов - (табл. 4.4).
Таблица 4.4
Рис.4.8
Матрица переходов RS – триггера приведена на рис. 4.9, а условное обозначение на рис. 4.10. Символ «*» определяет любое значение.
| q(t) →q(t+1) | S R |
| 0 → 0 | 0 * |
| 0 → 1 | 1 0 |
| 1 → 0 | 0 1 |
| 1 → 1 | * 0 |
Рис. 4.9
Рис. 4.10
JK триггер.
J – вход установки «1» (jump), т.е. при подаче «1» на вход J, триггер переходит в состояние «1» (установка 1).
K – вход установки «0» (kill), т.е. при подаче «1» на вход K, триггер переходит в состояние «0» (сброс в 0).
Подача на входы J и K двух единиц одновременно меняет состояние триггера на противоположное.
Подача на входы J и K двух нулей одновременно не меняет состояние триггера.
Граф автомат Мура, задающий JK – триггер (рис. 4.11). Дуги графа помечены значениями входов J K. Таблица переходов - (табл. 4.5).
Таблица 4.5
Рис. 4.11
Матрица переходов JK – триггера приведена на рис. 4.12, а условное обозначение на рис. 4.13. Символ «*» определяет любое значение.
| q(t) →q(t+1) | J K |
| 0 → 0 | 0 * |
| 0 → 1 | 1 * |
| 1 → 0 | * 1 |
| 1 → 1 | * 0 |
Рис. 4.12
Рис. 4.13
4.2. Пример структурного синтеза синхронного автомата
Автомат называется синхронным, если его состояния меняются в строго определенные моменты времени, задаваемые с помощью специальных сигналов синхронизации.
Пусть задан абстрактный автомат Мили в виде графа (рис. 4.14) или таблицы переходов и выхода (табл. 4.6). Этот автомат был получен ранее в результате выполнения абстрактного этапа канонического метода синтеза.
Рис. 4.14
Таблица 4.6
| pj si | | |
| s0 | s1 /0 | s1 /0 |
| s1 | s2 /0 | s2 /0 |
| s2 | s0 /1 | s0 /0 |
Требуется построить функционально логическую схему автомата из логических элементов типа «И» (конъюнкторов) и типа «НЕ» (инверторов). В качестве элемента памяти задан RS – триггер.
Логическая схема автомата должна иметь минимальное число логических элементов.
Исходный абстрактный автомат имеет следующие алфавиты:
P = {0,1}, W = {0,1} и их кодирование проводить не надо т.к. они двоичные.
Множество состояний S = {s0, s1, s2}. Для кодирования трех состояний достаточно два разряда. Произвольно закодируем состояния следующим образом (табл. 4.7) и заменим в исходной таблице переходов и выхода (табл. 4.6) абстрактные символы состояний на соответствующие им коды. Полученная кодированная таблица переходов и выходов (табл. 4.8).
Таблица 4.7 Таблица 4.8
| | y1 y2 |
| s0 | 0 1 |
| s1 | 1 1 |
| s2 | 1 0 |
| x y1y2 | | |
| 0 1 | 11 /0 | 11 /0 |
| 1 1 | 10 /0 | 10 /0 |
| 1 0 | 01 /1 | 01 /0 |
Структурная схема для исходного автомата представлена на рис. 4.15.
 1 1 |
 2 2 |
Рис. 4.15
Из структурной схемы автомата на рис. 4.15 видно, что комбинационная схема реализует систему следующих пяти булевых функций: z – функция выхода, y’S1, y’R1 - функции возбуждения триггера T1, y’S2, y’R2 - функции возбуждения триггера T2, зависящих от трех переменных: х, у1, у2. Для определения функции выхода z достаточно кодированной таблицы переходов и выходов (табл. 4.8), а для определения функций возбуждения y’S1, y’R1, y’S2, y’R2 необходима еще матрица переходов используемого триггера (рис. 4.9).
Для упрощения нахождения этих булевых функций удобно использовать таблицу функций возбуждения и выходов (табл. 4.9), которая строится предварительно на основании кодированной таблицы переходов и выходов (табл. 4.8), и матрицы переходов триггера (в рассматриваемом примере рис. 4.9). Для этого в кодированной таблице переходов и выходов анализируются пары кодов состояний триггеров (до перехода и после перехода) и в соответствующей клетке таблицы функций необходимо вместо кодов состояний записать значения функций возбуждения триггера, которые приведут триггер в требуемое состояние. Значение функции выхода переписывается из кодированной таблицы переходов и выходов. Значения этих функций записываются в клетках таблицы функций следующим образом: y’S1y’R1, y’S2y’R2 / z.
Например, для реализации перехода автомата из состояния с кодом 01 в состояние с кодом 11 по x = 0 необходимо перевести триггер Т1 из 0 в 1 и сохранить единичное состояние триггера Т2. Для этого следуя матрице переходов RS - триггера (рис. 4.9) необходимы следующие значения функций возбуждения y’S1 = 1, y’R1 = 0, y’S2 = *, y’R2 = 0 и если при этом z = 0, то в верхнюю, левую клетку табл. 4.9 записывается: 10, *0 / 0.
Таблица 4.9 Таблица 4.10
| x y1y2 | | 1 |
| 0 1 | 10, *0 / 0 | 10, *0 / 0 |
| 1 1 | *0, 01 / 0 | *0, 01 / 0 |
| 1 0 | 01,10 / 1 | 10,01 / 0 |
Далее для определения системы булевых функций возбуждения и выходов необходимо построить пять карт Карно для трех переменных и, последовательно просматривая по клеткам полученную таблицу функций возбуждения и выходов (табл. 4.9), одновременно заполняются все пять карт Карно. Например, значения из верхней, левой клетки таблицы функций переписываются в верхнюю, правую клетку соответствующих карт Карно. Карта Карно для функции выхода – табл. 4.10, а карты Карно для функций возбуждения – табл. 4.11, 4.12, 4.13, 4.14.
Таблица 4.1
1 Таблица 4.1
2
Таблица 4.13 Таблица 4.14
После совместной минимизации полученной системы булевых функций с помощью карт Карно получается следующая система булевых функций:
z =  2;
2;
y’S1 =  1, y’R1 =
1, y’R1 =  2;
2;
y’S2 =  2, y’R2 = y1 y2.
2, y’R2 = y1 y2.
Далее происходит реализация минимальной системы булевых функций из заданных логических элементов, т.е. строится комбинационная схема автомата. К выходам логических схем, реализующих функции возбуждения, подключаются заданные элементы памяти составляющие блок памяти автомата.
В результате получается следующая функциональная схема автомата (рис. 4.16). Для проверки правильности ее построения необходимо протестировать его работу на конкретном входном слове. На рис. 4.16 показана работа автомата по переработке входного слова 1 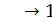 0. Это слово перерабатывается в выходное слово 0
0. Это слово перерабатывается в выходное слово 0  0
0  1. Указывается также последовательность значений на выходе каждого логического элемента, причем на выходе триггеров указано на одно значение больше. Это значение соответствует коду начального состояния автомата s0 = 01, в которое он предварительно должен быть установлен (рис. 4.16).
1. Указывается также последовательность значений на выходе каждого логического элемента, причем на выходе триггеров указано на одно значение больше. Это значение соответствует коду начального состояния автомата s0 = 01, в которое он предварительно должен быть установлен (рис. 4.16).
0  0 0  1 1 |
 1 1 |
 2 2 |
 2 2 |
 2 2 |
 2 2 |
 1 1 |
0  0 0  1 1 |
0  1 1  0 0 |
0  0 0  1 1 |
1  0 0  0 0 |
0  0 0  1 1 |
1  0 0 |
Рис. 4.16
Для обеспечения устойчивой работы автомата в его схеме используется сигнал синхронизации – с. При с = 0 значения функций возбуждения непосредственно на входах триггеров равны 0 . Это соответствует режиму хранения триггеров и следовательно автомат остается в том же состоянии. При с = 1 вычисленные в комбинационной схеме значения функций возбуждения непосредственно поступают на входы триггеров т.е. : S1 = y’S1, R1 = y’R1, S2 = y’S2, R2 = y’R2 и триггеры переключаются и таким образом автомат переходит в новое состояние.
Длительность с = 1 должна быть достаточной, чтобы сработал конъюнктор на входе триггера и переключились сами триггеры.
В момент времени, когда переключаются триггеры, значения функций возбуждения не должны меняться иначе триггер может перейти в незапланированное состояние. В это же время меняются значения на выходе триггеров y1, y2. и они по линии обратной связи поступают на входы комбинационной схемы и могут привести к изменению значений функций возбуждения и выходов. Следовательно, длительность сигнала
с = 1 должна быть ограничена так, чтобы новые значения y1, y2 не успели поступить на входы триггера в этом же автоматном такте.
Пусть: ∆τ – время задержки в срабатывании одного логического элемента и если время срабатывания триггера 2∆τ, то длительность T1, когда значение с = 1, находится в интервале: 3∆τ < T1 ≤ 3,5∆τ
Считывать значение функции выхода z можно лишь тогда, когда y1, y2 и x не меняются и z имеет установившееся значение после завершения всех переходных процессов в схеме. Это происходит при с = 1 ,т.е. функции возбуждения и выходов необходимо считывать по фронту сигнала синхронизации.
Входной сигнал x необходимо менять по спаду сигнала синхронизации, т.е. при с = 0, как только автомат перейдет в новое состояние. Длительность T0, когда значение с = 0, определяется временем формирования значений функций возбуждения и выходов в комбинационной схеме, определяется числом логических элементов в самой длинной цепочке этой схемы.
Построение временной диаграммы работы схемы автомата.
Временн  я диаграмма отображает работу схемы во времени и строится одновременно с ее логическим моделированием.
я диаграмма отображает работу схемы во времени и строится одновременно с ее логическим моделированием.
Построение временн  й диаграммыначинается с расчета параметров сигнала синхронизации т.е. определения величин T1, T0 и построение сигнала синхронизации на первой оси времени в виде последовательности прямоугольных импульсов, высота которых соответствует логической единице, а ширина – величине T1. Расстояние между импульсами соответствует величине T0. Импульсы имеют правильную форму, так как формируются генератором синхросигналов.
й диаграммыначинается с расчета параметров сигнала синхронизации т.е. определения величин T1, T0 и построение сигнала синхронизации на первой оси времени в виде последовательности прямоугольных импульсов, высота которых соответствует логической единице, а ширина – величине T1. Расстояние между импульсами соответствует величине T0. Импульсы имеют правильную форму, так как формируются генератором синхросигналов.
В момент времени t0 автомат должен быть установлен в начальное состояние s0 = 01, т.е. y1 = 0, y2 = 1. Линии, определяющие эти значения, можно продолжить на соответствующих осях до момента времени t1 так как при с = 0 триггер не может изменить свое состояние
Далее задается входная последовательность по x: 1 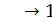 0, причем изменение сигнала происходит по спаду сигнала синхронизации в момент времени t4.
0, причем изменение сигнала происходит по спаду сигнала синхронизации в момент времени t4.
После нанесения на диаграмму входных воздействий вычисляются по комбинационной схеме для x = 1, y1 = 0, y2 = 1 значения функций возбуждения и выхода в момент времени t0. Эти значения:
y’S1 = 1, y’R1 = 0, y’S2 = 0, y’R2 = 0, z = 0 расставляются на схеме (рис. 4.16).
 1 1 |
 2 2 |
Рис. 4.17
Линии определенные этими значениями наносим на соответствующие оси временной диаграммы (рис. 4.17) до момента времени t1. Далее по фронту сигнала синхронизации, в момент t1 функции возбуждения поступают на входы триггеров и так как y’S1 = 1, то первый триггер y1 установится в 1, т.е. автомат из начального состояния с кодом 01 перейдет в новое состояние с кодом 11. На диаграмме стрелками указывается последовательность изменения значений сигналов. Одновременно со считыванием значений функций возбуждений считывается значение функции выхода z = 0.
Эти действия повторяются до момента t6, когда перестают поступать сигналы синхронизации c = 1 на вход схемы, автомат возвращается в начальное состояние s0 и прекращает работу по переработке слова.
На временной диаграмме (рис. 4.17) не показаны совпадающие сигналы так как: y’S1 =  1, y’R1 = y’S2 =
1, y’R1 = y’S2 =  2.
2.
Недостатком рассмотренной схемной реализации синхронного автомата является то, что достаточно сложно для него построить генератор синхросигналов с такими жесткими требованиями к их длительностиалов.
 = {α1, α2, …, αn}
= {α1, α2, …, αn}  = {β1, β2,…, βm}
= {β1, β2,…, βm}  = {γ1, γ2,…, γq}
= {γ1, γ2,…, γq}  ,
,  ) … y’q = φ’q (
) … y’q = φ’q (  ,
,  )
)  ) … zm = ψm’ (
) … zm = ψm’ (  )
)  ,
,  ) … zm = ψm’ (
) … zm = ψm’ (  ,
,  )
)  ,
,  – множества двоичных наборов соответствующие алфавитам абстрактного автомата.
– множества двоичных наборов соответствующие алфавитам абстрактного автомата.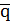
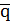
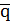
 1
1  2
2  2;
2; 1, y’R1 =
1, y’R1 =  2;
2; 2, y’R2 = y1 y2.
2, y’R2 = y1 y2.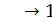 0. Это слово перерабатывается в выходное слово 0
0. Это слово перерабатывается в выходное слово 0  0
0  1. Указывается также последовательность значений на выходе каждого логического элемента, причем на выходе триггеров указано на одно значение больше. Это значение соответствует коду начального состояния автомата s0 = 01, в которое он предварительно должен быть установлен (рис. 4.16).
1. Указывается также последовательность значений на выходе каждого логического элемента, причем на выходе триггеров указано на одно значение больше. Это значение соответствует коду начального состояния автомата s0 = 01, в которое он предварительно должен быть установлен (рис. 4.16). 0
0  1
1  1
1  2
2  2
2  2
2  2
2  1
1  0
0  1
1  1
1  0
0  0
0  1
1  0
0  0
0  0
0  0
0 
 0
0  0
0 
 1
1  1
1 
 1
1  0
0 
 0
0  1
1 
 0
0  1
1  0
0  я диаграмма отображает работу схемы во времени и строится одновременно с ее логическим моделированием.
я диаграмма отображает работу схемы во времени и строится одновременно с ее логическим моделированием. й диаграммыначинается с расчета параметров сигнала синхронизации т.е. определения величин T1, T0 и построение сигнала синхронизации на первой оси времени в виде последовательности прямоугольных импульсов, высота которых соответствует логической единице, а ширина – величине T1. Расстояние между импульсами соответствует величине T0. Импульсы имеют правильную форму, так как формируются генератором синхросигналов.
й диаграммыначинается с расчета параметров сигнала синхронизации т.е. определения величин T1, T0 и построение сигнала синхронизации на первой оси времени в виде последовательности прямоугольных импульсов, высота которых соответствует логической единице, а ширина – величине T1. Расстояние между импульсами соответствует величине T0. Импульсы имеют правильную форму, так как формируются генератором синхросигналов.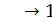 0, причем изменение сигнала происходит по спаду сигнала синхронизации в момент времени t4.
0, причем изменение сигнала происходит по спаду сигнала синхронизации в момент времени t4. 1
1  2
2  1, y’R1 = y’S2 =
1, y’R1 = y’S2 =  2.
2.