Исходными данными в каноническом методе синтеза на абстрактном этапе является таблица соответствия между входными и выходными словами.
Результатом абстрактного этапа является абстрактный автомат, представленный в виде графа или таблицы переходов и выхода.
Этап абстрактного синтеза состоит из двух подэтапов:
1. Построение по алфавитному оператору абстрактного автомата;
2. Минимизация числа состояний абстрактного автомата.
Таблица, устанавливающая соответствие между входными и выходными словами, которые перерабатывает автомат, называется алфавитным оператором.
Рис. 3.1
Индексы (рис. 3.1) указывают на соответствие входных и выходных символов автоматным тактам, а не на различие между буквами.
Пусть P = {0 , 1}, W = {0 , 1}.
В (табл. 3.1) приведен пример алфавитного оператора, где индексы соответствуют автоматным тактам и задают последовательность считывания и выдачи символов. с числом разрядов
Таблица 3.1
| p0 p1 p2 p3 | w0 w1 w2 w3 |
| 0 0 0 0 0 0 1 1 0 1 0 0 0 0 1 0 | 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 |
Алфавитный оператор называется автоматным, если он удовлетворяет следующим условиям:
1. однозначно отображает входные слова в выходные;
2. удовлетворяет условию полноты, т.е. любой начальный отрезок  допустимого слова
допустимого слова  также допустим (
также допустим ( 
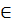 Pg*);
Pg*);
3. сохраняет длину преобразуемого слова;
4. осуществляет преобразование совпадающих начальных отрезков входных слов в совпадающие начальные отрезки соответствующих выходных слов.
Если алфавитный оператор является автоматным, то можно построить, реализующий его конечный автомат.
Для преобразования неавтоматного алфавитного оператора к автоматному виду используются две операции: выравнивание и пополнение.
Операция выравнивание используется, если нарушено третье условие автоматности оператора и состоит в приписывании специального пустого символа « е» справа к входному или слева к выходному слову, при этом этот пустой символ добавляется во входной и выходной алфавиты
В (табл. 3.2) приведен пример применения операция выравнивание к алфавитному оператору, преобразующему двухбуквенные слова в однобуквенные.
Таблица 3. 2
Операция пополнение используется, если нарушено четвертое условие автоматности, и состоит в приписывании пустого символа « e » справа к входному слову и одновременно слева к выходному слову.
В (табл. 3.3) приведен пример применения операция выравнивание к алфавитному оператору, преобразующему двухбуквенные слова в двухбуквенные.
Таблица 3. 3
| p0 | p1 | p1 | w0 | w1 | w2 |
| | | e | e | | |
| | | e | e | | |
| | | e | e | | |
| | | e | e | | |
Первоначально одинаковые начальные отрезки из одной буквы 0 в первом и втором входном слове преобразуется в 0 в первом и в 1 во втором выходном слове, т.е. нарушено четвертое условие автоматности, поэтому к этим входным словам справа и к соответствующим выходным словам слева дописывается пустой символ « e ». После этого одинаковые начальные отрезки первого и второго входного слова преобразуются в одинаковые начальные отрезки выходных слов из буквы « e ». Тоже самое необходимо проделать с третьим и четвертым словом.
Алфавитные операторы могут быть заданы двумя способами: табличным и графическим.
Табличный способ устанавливает соответствие между входными и выходными словами в форме таблицы.
В графическом способе оператор представляется в виде дерева нагруженного входными и выходными словами. Дерево это граф без циклов. Путь от корня (начальной вершины) к листу (конечной вершине) дерева соответствует одному входному слову. Число ярусов дерева соответствует длине входного слова.
Построение дерева входных последовательностей.
Пусть P = {p0 , p1 , … , pn} – входной алфавит.
Алгоритм построения дерева состоит из выполнения следующих шагов:
1. фиксируется начальная вершина, которая называется корнем дерева;
2. из вершины проводятся n дуг, каждая из которых помечается буквой входного алфавита;
3. на концах дуг строится n вершин;
4. из каждой построенной вершины проводятся n дуг и так далее;
5. последняя висячая вершина (лист) – называется конечной вершиной.
Для построения автомата по автоматному алфавитному оператору необходимо выполнить следующие действия :
1. построить дерево входных последовательностей.
2. отметить все вершины дерева символами состояний автомата si, при этом корень пометить символом начального состояния s0, а все висячие вершины (листья) символами конечного состояния sk.
3.1. для получения графа автомата Мура вершины дерева отметить символами соответствующих выходных слов;
3.2. для получения графа автомата Мили отметить дуги символами соответствующих выходных слов
4. все конечные вершины совместить в одну.
В результате выполнения этого подэтапа получается граф полностью определенного абстрактного автомата.
Минимизация числа состояний абстрактного автомата, заданного графом переходов .
Уменьшение числасостояний полностью определенного абстрактного автомата можно осуществить за счет объединения эквивалентных состояний
Два состояния автомата называются эквивалентными, если при переходе из них по одинаковым входным символам в одно и то же состояние происходит выдача одинаковых выходных символов.
На (рис. 3.2) представлен фрагмент графа автомата Мили с двумя эквивалентными состояниями si и sj ,что обозначается: si  sj.
sj.
Рис. 3.2
После объединения этих эквивалентных состояний в одно, обозначенное символом sij ,получается фрагмент графа автомата Мили (рис. 3.3) с меньшим числом состояний.
Рис. 3.3
Автоматом многократного действия называется автомат, который после переработки входного слова будет готов к приему следующего.
Для получения автомата многократного действия необходимо его начальную вершину совместить с конечной.
Пример построения абстрактного автомата Мили по автоматному алфавитному оператору, заданного таблицей (табл. 3.4).
Таблица 3. 4
Из таблицы определяется входной и выходной алфавит:
P = {0 , 1}, W = {0 , 1}.
Строится дерево входных последовательностей (рис. 3.4).
Рис.3.4
Дерево входных последовательностей с вершинами размеченными символами состояний (рис. 3.5) формирует следующее множество состояний: S = {s0 , s1 , s2 , s3 , s4 , s5 , s6 , sk }.
Рис.3.5
Дерево с дугами, размеченными соответствующими выходными символами (рис. 3.6).
Рис.3.6
После объединения в одну всех вершин, помеченных символом sk , получается граф автомата Мили (рис. 3.7).
Рис.3.7
Вторым этапом абстрактного синтеза является минимизация числа состояний. Из анализа переходов в конечное состояние sk видно, что существуют две пары эквивалентных состояний s3  s4 и s5
s4 и s5  s6. После объединения этих состояний получается граф автомата Мили (рис. 3.8).
s6. После объединения этих состояний получается граф автомата Мили (рис. 3.8).
Рис.3.8
Из анализа переходов в конечное состояние sk на рис.3.8 видно, что новые состояния s34 и s56 также эквивалентны, т.е. s34  s56. После их объединения получается граф автомата Мили (рис. 3.9).
s56. После их объединения получается граф автомата Мили (рис. 3.9).
Рис.3.9
Из анализа переходов в состояние s3456 видно, что s1  s2 и после их объединения получается граф автомата Мили (рис. 3.10).
s2 и после их объединения получается граф автомата Мили (рис. 3.10).
Рис.3.10
Для получения автомата многократного действия совмещаются состояния s0 и sk и после их переобозначения получается граф автомата Мили (рис. 3.11).
Рис. 3.11
Графу автомата Мили (рис. 3.11) соответствует таблица переходов и выхода (табл. 3.5).
Таблица 3.5
| pi sj | | |
| s0 | s1/0 | s1/0 |
| s1 | s2/0 | s2/0 |
| s2 | s0/1 | s0/0 |
Для проверки работы полученного автомата промоделируем его работу по переработке входного слова: 1 1 0. Результат работы приведен в табл. 3.6.
Таблица 3.6
| tk | t0 | t1 | t2 | |
| si | s0 | s1 | s2 | s0 |
| pj | | | | |
| wm | | | | |
Таким образом, входное слова: 1 1 0 перерабатывается в выходное слова: 0 0 1, что соответствует заданному алфавитному оператору.
3.2. Минимизация числа состояний полностью определенного автомата
В примере была рассмотрена минимизация автомата Мили на его графе, но это трудно проделать при большом числе состояний.
Пусть полностью определенный автомат A, имеющий k состояний, задан таблицей переходов и выхода. Требуется построить эквивалентный ему автомат A* c числом состояний k*, причем k* ≤ k.
Минимизация числа состояний полностью определенного автомата осуществляется за счет объединения эквивалентных состояний.
Два состояния s’ и s” называются эквивалентными, если любую входную последовательность автомат перерабатывает в одинаковые выходные последовательности, независимо от того какой из этих двух состояний s’ или s” выбраны в качестве начального т.е. s’≡ s”.
Отношение эквивалентности обладает следующими свойствами:
1. рефлексивность, т.е. s’ ≡ s’;
2. симметричность, т.е. если s’≡ s”, то из этого следует: s”≡ s’;
3. транзитивность, т.е. если s’≡ sk и s”≡ sk, то из этого следует что: s’ ≡ s”.
Отношение эквивалентности разбивает все множество состояний S на классы эквивалентности: S = C1 U C2 U C3 U…U Cq.
Класс эквивалентности Ci 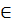 S - это подмножество состояний попарно эквивалентных между собой, причем . Ci ∩ Cj = Ø, если i ≠ j, т.е. пересечение любых двух классов эквивалентности представляет собой пустое множество и следовательно каждое состояние может входить только в один класс эквивалентности.
S - это подмножество состояний попарно эквивалентных между собой, причем . Ci ∩ Cj = Ø, если i ≠ j, т.е. пересечение любых двух классов эквивалентности представляет собой пустое множество и следовательно каждое состояние может входить только в один класс эквивалентности.
На рис. 3.12 приведен тривиальный пример эквивалентных состояний s’≡ s” и их объединения, который был использован ранее при переходе от алфавитного оператора к графу автомата.
Рис. 3.12
На рис. 3.13 приведен пример фрагмента графа автомата, в котором эквивалентность состояний s’ и s”не являетсястоль очевидной.
Рис. 3.13
На рис. 3.14 приведен фрагмент графа после объединения s’ и s”.
Рис. 3.14
Два необходимых условия эквивалентности состояний автомата Мили.
Два состояния s’ и s”являются эквивалентными, если:
1. при переходе из этих состояний под воздействием любого одинакового входного символа pk вырабатываются одинаковые выходные символы, т.е: ψ’(s’,pk) = ψ”(s”,pk);
2. при переходе из этих состояний под воздействием любого одинакового входного символа pk переход осуществляется в одно и то же или в эквивалентные состояния, т.е. если
si = φ’(s’,pk) и sj = φ”(s”,pk), то следует, что si ≡ sj.
Алгоритм минимизации числа состояний полностью определенного с помощью треугольной матрицы.
Задан таблицей переходов и выхода полностью определенный автомат Мили, имеющий k –состояний.
Алгоритм состоит из выполнения следующих шагов:
1. Строится треугольная матрица без диагональных элементов, столбцы которой нумеруются слева направо индексами состояний с 1 до k -1, а строки матрицы сверху вниз с 2 до k;
2. Любой клетки матрицы с координатами i и j соответствовать пара состояний si и sj. Последовательно просматривая таблицу переходов матрица заполняются следующим образом:
a) если для пары si и sj невыполнимо первое условие эквивалентности, то в клетку ставят «×», это означает, что эти состояния заведомо; неэквивалентны;
b) если для пары состояний si и sj выполняется первое условие, но еще не известно выполняется ли второе, т.к. переходы осуществляется в разные состояния, то в клетку записывают номера состояний от эквивалентности которых зависит эквивалентность рассматриваемой пары;
c) если для пары состояний si и sj сразу выполняются оба условия, то клетка оставляется пустой, то означает, что эти состояния заведомо эквивалентны;
3. заполненная треугольная матрица, последовательно просматривается по клеткам, содержащим номера пар состояний и если известно, что эти номера соответствуют не эквивалентным состояниям, то в этой клетки ставят «×». Просмотр матрицы продолжается до тех пор пока не перестанут появляться новые пары неэквивалентных состояний;
4. Из треугольной матрицы выписываются все пары эквивалентных состояний (где не содержится «×») и из них образуются классы эквивалентности;
5. Каждому классу эквивалентности ставится в соответствие символ нового состояния и переписывается исходная таблица переходов и выхода.
Пример минимизации автомата Мили заданного таблицей переходов и выхода (табл. 3.7).
P = {a, b, c}, W = {1, 2}, S = {s1, s2, s3, s4, s5, s6, s7, s8}.
В таблице переходов и выхода (табл. 3.7) для наглядности вместо символов состояний указаны только их индексы.
| pk si | a | b | c |
| | 4 / 1 | 2 / 2 | 5 / 1 |
| | 5 / 2 | 1 / 1 | 4 / 2 |
| | 3 / 2 | 5 / 1 | 4 / 2 |
| | 5 / 1 | 8 / 2 | 4 / 2 |
| | 7 / 1 | 2 / 2 | 1 / 1 |
| | 1 / 1 | 3 / 2 | 4 / 2 |
| | 5 / 1 | 3 / 2 | 7 / 2 |
| | 3 / 2 | 5 / 1 | 6 / 2 |
Таблица 3.7
Рис. 3.15
На рис. 3.15 приведена треугольная матрица, заполненная по изложенному выше алгоритму. Клетки, не содержащие «×» соответствуют следующим парам эквивалентных состояний: 1 ≡ 5, 3 ≡ 8, 4 ≡ 6, 4 ≡ 7,6 ≡ 7 и из них можно образовать следующие классы эквивалентности:
C1 = {1 , 5}, C2 = {2}, C3 = {3 , 8}, C4 = {4 , 6 , 7}.
Каждому классу сопоставляется символ нового состояния:
C1 – s’1, C2 – s’2, C3 – s’3, C4 – s’4. Далее в исходной таблице переходов символ старого состояния, заменяется на символ нового состояния, который соответствует классу, в который это старое состояние входит. В результате получается таблица переходов и выхода (табл. 3.8).
После объединения в ней одинаковых строк получается таблица переходов и выхода минимального автомата Мили (табл. 3.9), с числом состояний k* = 4 вместо k = 8 в исходном автомате.
Таблица 3.8
| pk si | a | b | c |
| 1’ | 4’/ 1 | 2’/ 2 | 1’/ 1 |
| 2’ | 1’/ 2 | 1’/ 1 | 4’/ 2 |
| 3’ | 3’/ 2 | 1’/ 1 | 4’/ 2 |
| 4’ | 1’/ 1 | 3’/ 2 | 4’/ 2 |
| 1’ | 4’/ 1 | 2’/ 2 | 1’/ 1 |
| 4’ | 1’/ 1 | 3’/ 2 | 4’/ 2 |
| 4’ | 1’/ 1 | 3’/ 2 | 4’/ 2 |
| 3’ | 3’/ 2 | 1’/ 1 | 4’/ 2 |
Таблица 3.9
| pk si | a | b | c |
| 1’ | 4’/ 1 | 2’/ 2 | 1’/ 1 |
| 2’ | 1’/ 2 | 1’/ 1 | 4’/ 2 |
| 3’ | 3’/ 2 | 1’/ 1 | 4’/ 2 |
| 4’ | 1’/ 1 | 3’/ 2 | 4’/ 2 |
 допустимого слова
допустимого слова  также допустим (
также допустим ( 
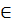 Pg*);
Pg*); sj.
sj. s4 и s5
s4 и s5  s6. После объединения этих состояний получается граф автомата Мили (рис. 3.8).
s6. После объединения этих состояний получается граф автомата Мили (рис. 3.8). s56. После их объединения получается граф автомата Мили (рис. 3.9).
s56. После их объединения получается граф автомата Мили (рис. 3.9). s2 и после их объединения получается граф автомата Мили (рис. 3.10).
s2 и после их объединения получается граф автомата Мили (рис. 3.10).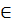 S - это подмножество состояний попарно эквивалентных между собой, причем . Ci ∩ Cj = Ø, если i ≠ j, т.е. пересечение любых двух классов эквивалентности представляет собой пустое множество и следовательно каждое состояние может входить только в один класс эквивалентности.
S - это подмножество состояний попарно эквивалентных между собой, причем . Ci ∩ Cj = Ø, если i ≠ j, т.е. пересечение любых двух классов эквивалентности представляет собой пустое множество и следовательно каждое состояние может входить только в один класс эквивалентности.