Множества истинности операций над предикатами

Обозначим через А_и , В_и множества истинности предикатов А(х), В(х) соответственно.

Нас будут интересовать множества истинности операций над этими предикатами.

Несложно показать при помощи рассуждений, что

[А(х)⋀В(х)]_и = А_и 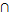В_и , (11.1)

[А(х)⋁В(х)]_и = А_и 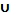В_и , (11.2)

[⅂А(х)]_и = (А_и)’ , (11.3)

[A(x) →В(х)]_и = [⅂А(х)⋁В(х)]_и = (А_и)’ 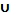В_и . (11.4)

Логическое следование предикатов

Определение 12.1.Пусть А(х) и В(х) – два предиката с общей областью определения. Если

A(x) →В(х) = И, (12.1)

то говорят, что В(х) логически следует из А(х).

Теорема 12.1. Предикат В(х) логически следует из предиката А(х) в том и только том случае, если выполнено включение множеств истинности:

А_и 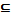В_и . (12.2)

Доказательство.См. рис. 7.1 и 7.2.

Замечание.Если выполнено соотношение (12.1), то говорят, что А(х) является достаточным условием для В(х), а В(х) является необходимым условием для А(х).

Квантор общности

Для определенности, будем в этом разделе говорить об одноместных предикатах , зависящих от переменной х; областью определения рассматриваемых предикатов считаем множество Х.

Определение 13.1.Квантором общности называют выражение

«для каждого х» (13.1)

- это краткая форма записи; либо выражение

«для каждого х 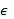Х» (13.1’)

- это подробная форма записи.

Для обозначения квантора общности используют специальный значок - перевернутую букву А (от английского слова all). В результате краткая запись приобретает вид: ( 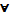х), а подробная запись – вид: ( 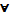х Х).

Замечание.Синонимами выражения (13.1) являются следующие словосочетания: «для всех х», «для любого х», «для всякого х». Аналогичное замечание справедливо и для выражения (13.1’).

Пусть теперь P(x) – некоторый предикат; постановка квантора общности перед ним превращает его в высказывание

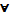( х)P(x) (13.2)

или, в подробной записи,

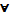( х Х)P(x) . (13.2’)

Замечание. Говорят, что квантор ( 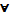х) связывает переменную х; в выражениях (13.2) и (13.2’) переменная х считается связанной (до постановки квантора ( 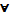х) эта же переменная была свободной).

Пример. Рассмотрим высказывание на естественном языке:

С: «Каждый человек носит шляпу».

Логическая структура этого предложения такова:

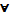( х Х)P(x);

здесь Х – множество всех людей, P(x) – предикат « х носит шляпу».

Нетрудно понять, что высказывание С ложно (т.к. существуют люди, которые не носят шляпу).

Квантор существования

Определение 14.1.Квантором существования называют выражение

«существует х такой, что» (14.1)

- это краткая форма записи; либо выражение

«существует х 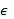Х такой, что» (14.1’)

- это подробная форма записи.

Замечание.В естественном языке роль квантора существования выполняют также словосочетания: «найдется х такой , что», «для некоторых х».

Для обозначения квантора существования используют специальный значок - отраженную по горизонтали букву Е (от английского слова exist). В результате краткая запись приобретает вид: ( 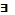х), а подробная запись – вид: ( 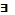х Х).

Квантор существования (как и квантор общности) связывает соответствующую переменную и превращает предикат в высказывание.

Пример. Рассмотрим высказывание:

D: «У некоторых людей четырнадцать ног».

Логическая структура этого предложения такова:

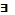( х Х)Q(x);

здесь Х – множество всех людей, Q(x) – предикат «х имеет четырнадцать ног».

Высказывание D, очевидно, ложно, так как не существует ни одного человека с 14-ю ногами.