Элементы теории дискретных структур. Логические (булевы) функции. Теорема о числе логических функций от нескольких аргументов.

ТЕОРЕМА (О разложении булевой функции по переменным)

F (x1,…, xm, x m+1,…,xn)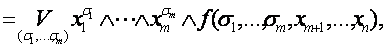

где дизъюнкция берется по всем возможным наборам (s₁,…,s_м).

ДОКАЗАТЕЛЬСТВО

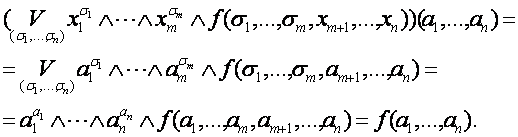ЗАМЕЧАНИЕ

Здесь доказывается, что некоторая формула реализует заданную функцию. Для этого до­статочно взять произвольный набор значений аргументов функции, вычислить на этомнаборе значение формулы, и если оно окажется равным значению функции на этом на­боре аргументов, то из этого следует доказываемое утверждение.

Дизъюктивные и конъюнктивные нормальные формы формул. Совершенные формы формул

Дизъюнкти́внаянорма́льнаяфо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любаябулева формула может быть приведена к ДНФ.^[1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.

Пример ДНФ: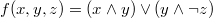

Конъюнкти́внаянорма́льнаяфо́рма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ.^[1] Для этого можно использовать: закон двойного отрицания, закон де Моргана, дистрибутивность.

Пример КНФ: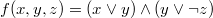

Совершенная конъюнктивная нормальная форма, СКНФ (англ. perfectconjunctivenormalform, PCNF) — это такая КНФ, которая удовлетворяет условиям: § в ней нет одинаковых простых дизъюнкций § каждая простая дизъюнкция полная

Пример СКНФ: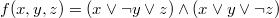

Соверше́ннаядизъюнкти́внаянорма́льнаяфо́рма (СДНФ) — это такая ДНФ, которая удовлетворяет трём условиям:

· в ней нет одинаковых элементарных конъюнкций

· в каждой конъюнкции нет одинаковых пропозициональных букв

· каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке.

Любая булева формула, не являющаяся тождественно ложной, может быть приведена к СДНФ, причем единственным образом^[1], то есть для любой выполнимой функции алгебры логики существует своя СДНФ, причём единственная.

Совершенная ДНФ этой функции:

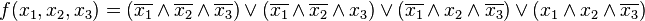
Полнота систем логических функций. Пример полных систем. Свойства линейности , двойственности и монотонности логических функций

Полнота систем логических функций и пример

Определение. Множество функций N называется функционально полной системой (ФПС), если любая булева функция представима суперпозицией функций из N.

Договоримся опускать аргументы при перечислении функций множества N и рассматривать термин ''система'' в данном контексте как синоним множества.

Пример 1. Множество N₁={ 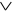, , 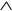^–} является функционально полной системой, так как любую булеву функцию, кроме константы 0, можно представить совершенной ДНФ, то есть суперпозицией функций из N₁ а константу 0 – формулой xx . •

Пример 2. Множество N₂={ 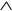, , 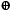1} является ФПС, так как любую булеву функцию можно представить полиномом Жегалкина, то есть суперпозицией функций из N₂, а полином 0 – формулой 1 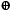1. •

Следующая теорема позволяет сводить вопрос о функциональной полноте одних систем к вопросу о полноте других систем.

Теорема о двух функционально полных системах. Если даны два множества N₁ и N₂ булевых функций и известно, что N₁ – функционально полная система, а каждая функция из N₁ представима суперпозицией функций из N₂, то N₂тоже является функционально полной системой.

Доказательство. Рассмотрим произвольную булеву функцию f(x₁, …, x_n). Она может быть представлена суперпозицией функций из множества N₁={f₀,f₁…, f_m}, так как N₁ – ФПС:

f(x₁, …, x_n)=f₀(f₁(x₁, …, x_n), …, f_m(x₁, …, x_n)).

По условию теоремы каждая из функций f₀, f₁ …, f_m может быть представлена суперпозицией функций из N₂, значит, функция f(x₁, …, x_n) представима суперпозицией функций из N₂, следовательно, N₂ – ФПС. •

Пример 1. N₁={ 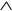, 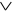^–, }, N₂={ 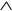, ^–}. Как показано ранее, N₁ – ФПС. Конъюнкция и инверсия содержатся в N₂, а дизъюнкция представима суперпозицией функций из N₂: x 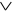y = 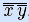, значит, N₂ – ФПС. •

Пример 2. N₁={ 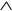, ^–}, N₂={↓ }. Как показано в предыдущем примере, N₁ – ФПС. Инверсия и конъюнкция могут быть представлены суперпозицией стрелки Пирса: x = x↓ x, xy = 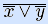= (x↓ x)↓ (y↓ y), следовательно N₂ – ФПС. •

Двойственная функци

Пусть имеем функцию f(a,b,c). Двойственной для нее является функцияf*= 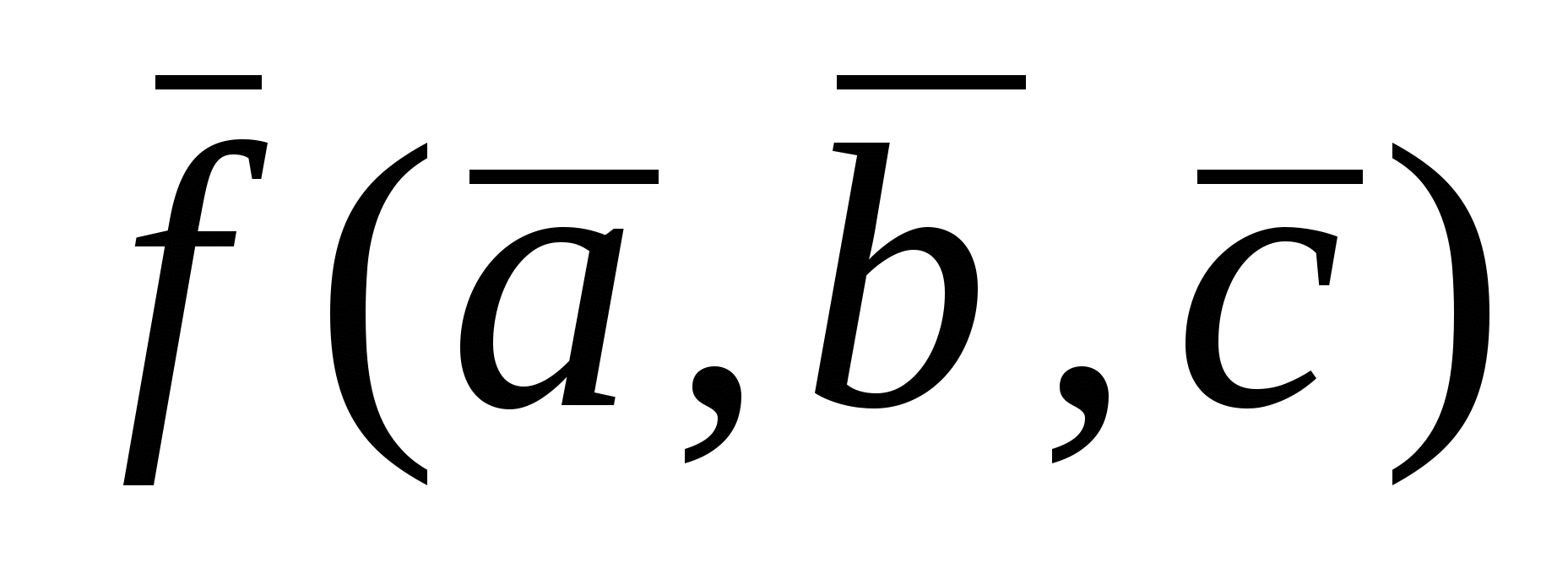, т.е. функция, в которой все аргументы и сама функция инвертированы.

Пример 2:

;

;

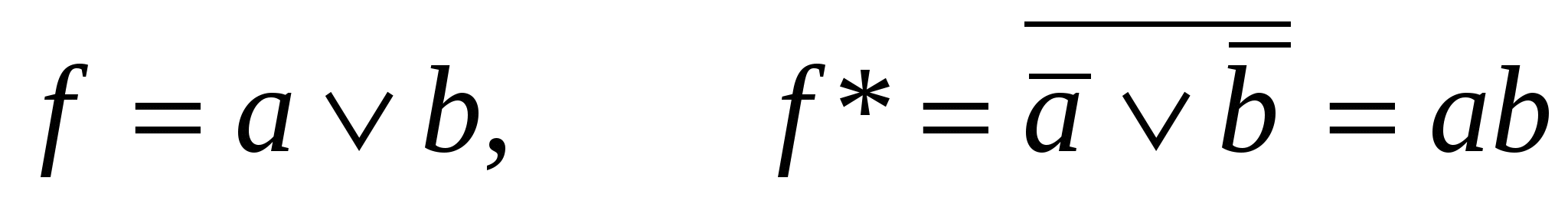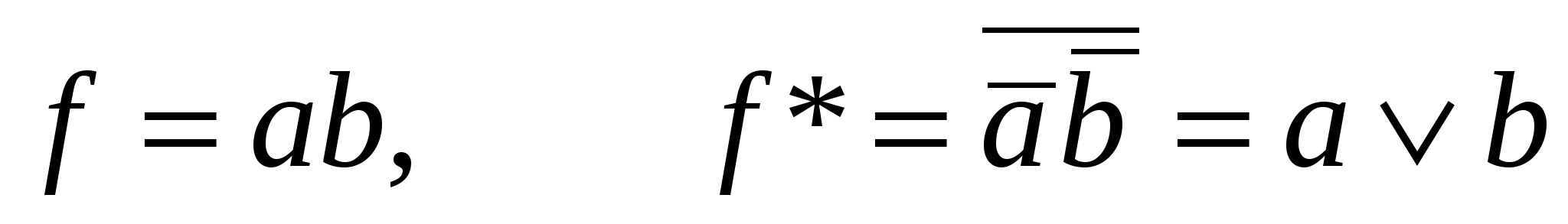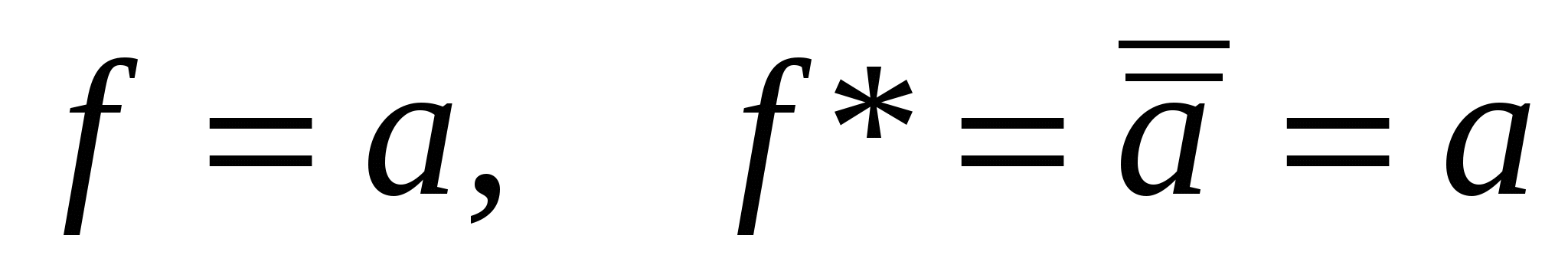– самодвойственная функция;

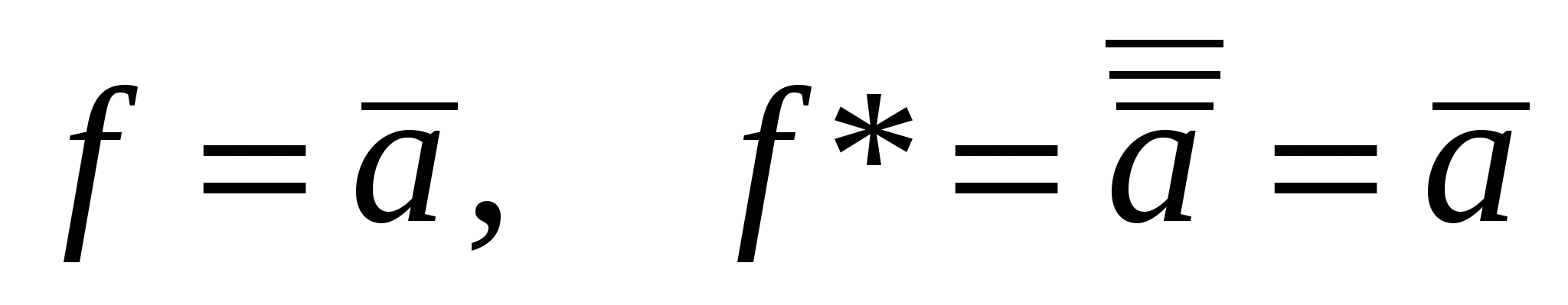– самодвойственная функция;

, = = =

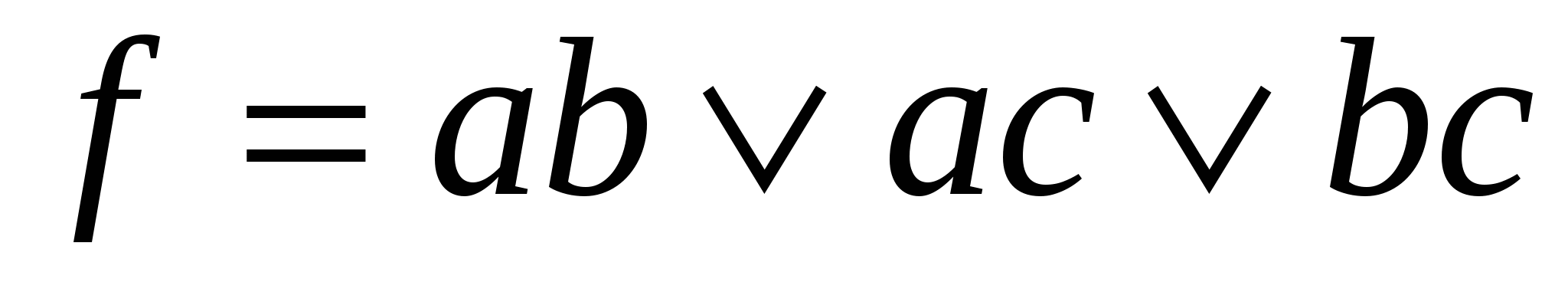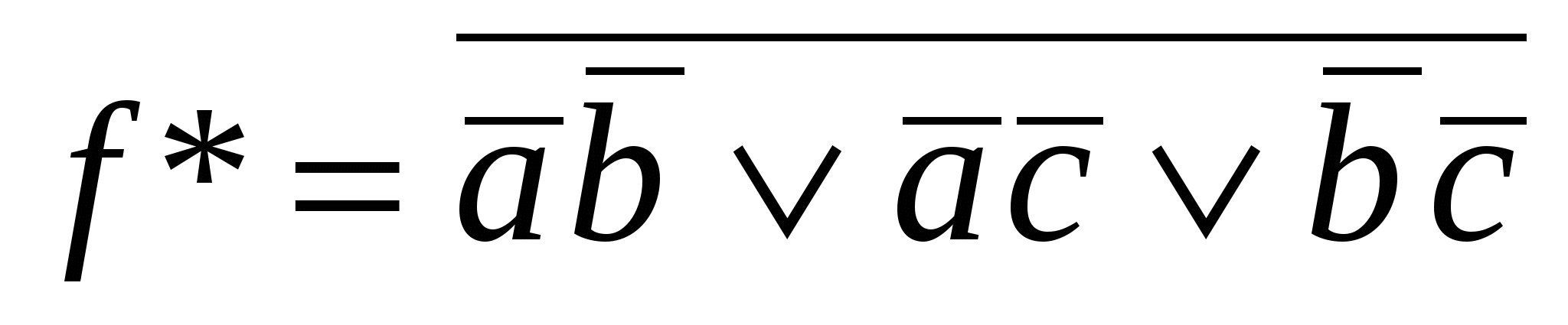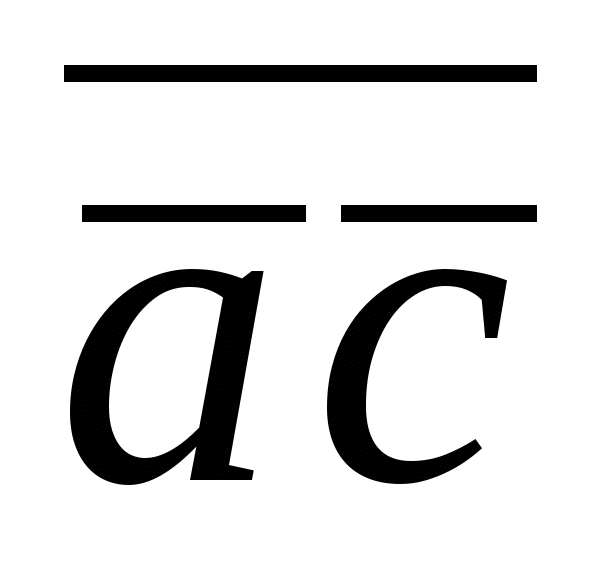
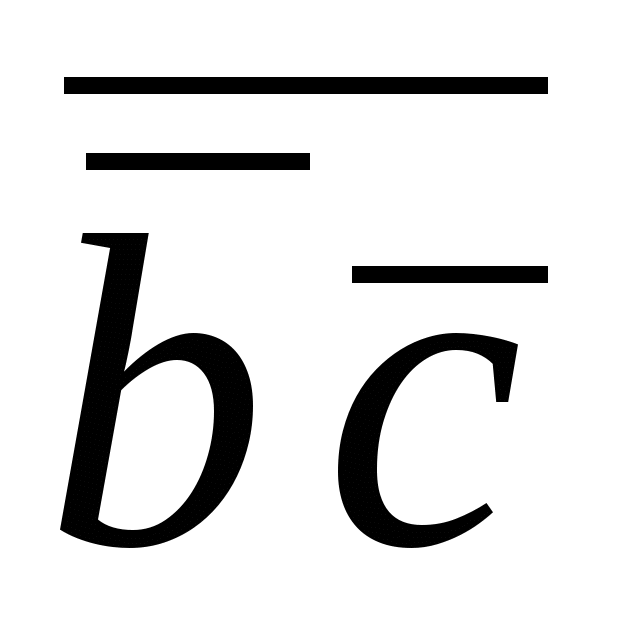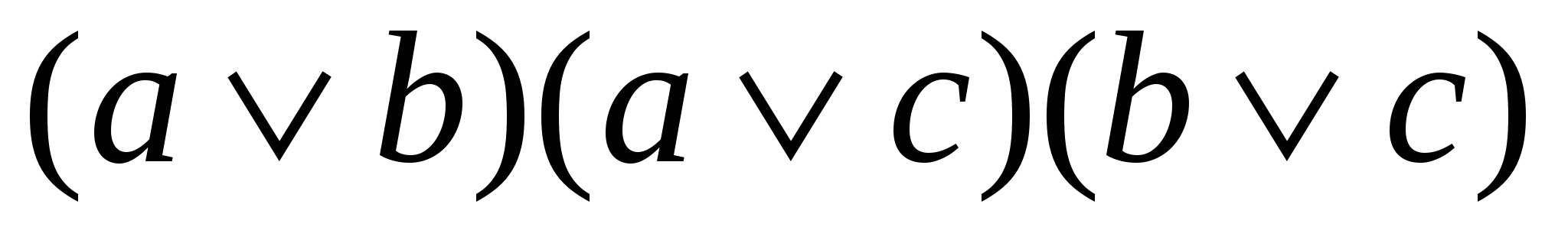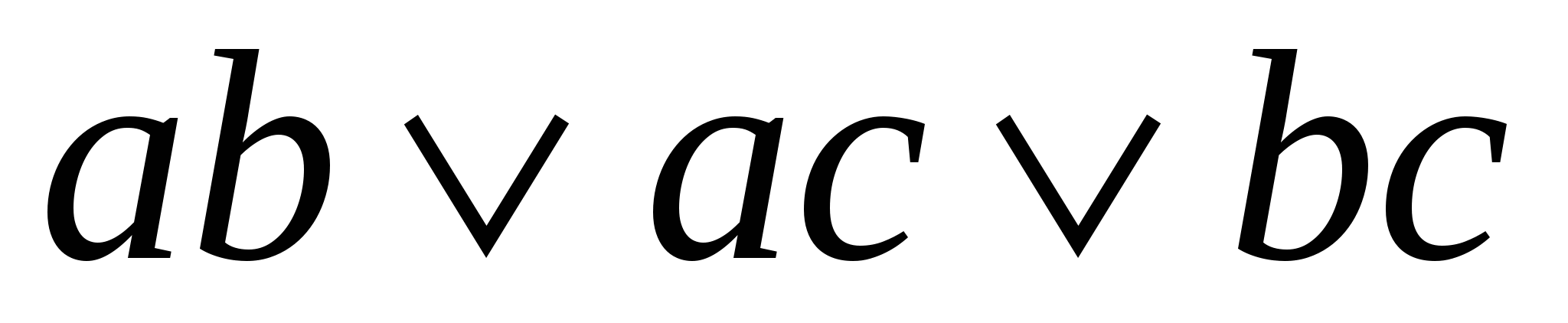= – самодвойственная функция.

Таким образом, для самодвойственной функции можно записать

f(a,b,c) = .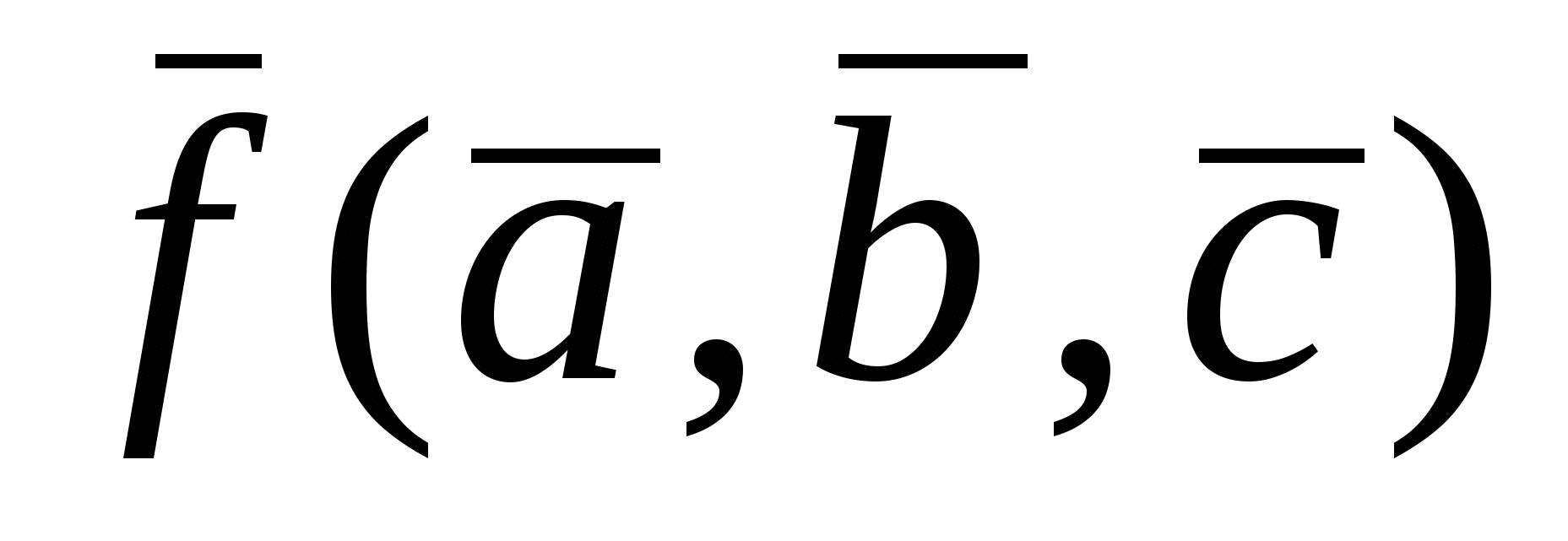

Монотонная функция

Выше мы установили для входных наборов отношение предшествования: Входной набор 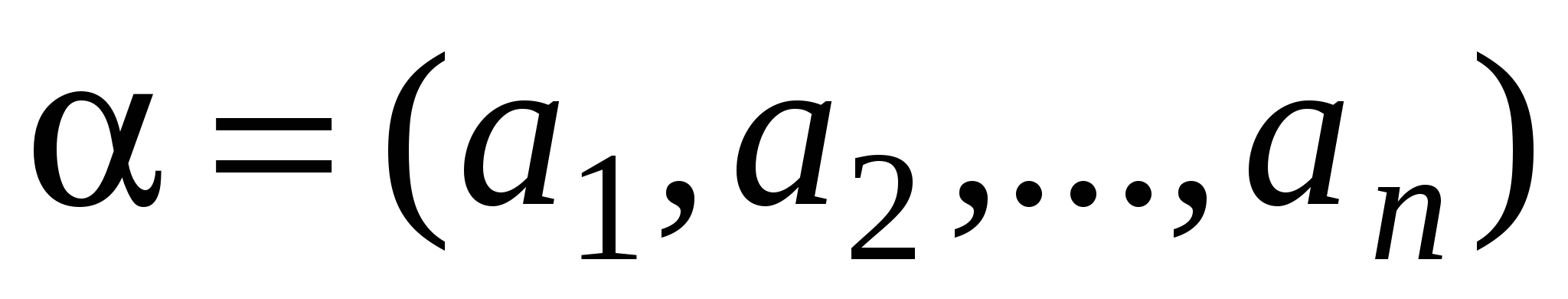предшествует набору 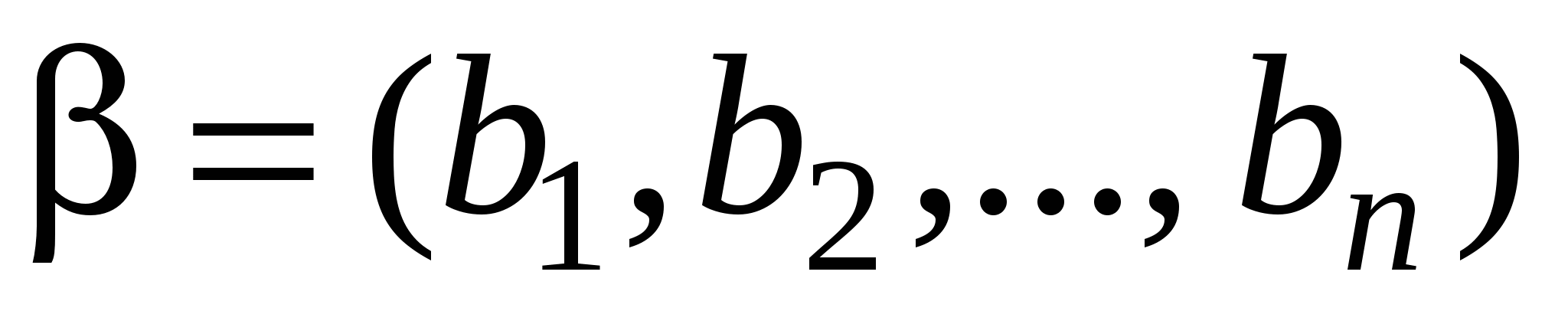(обозначается это так 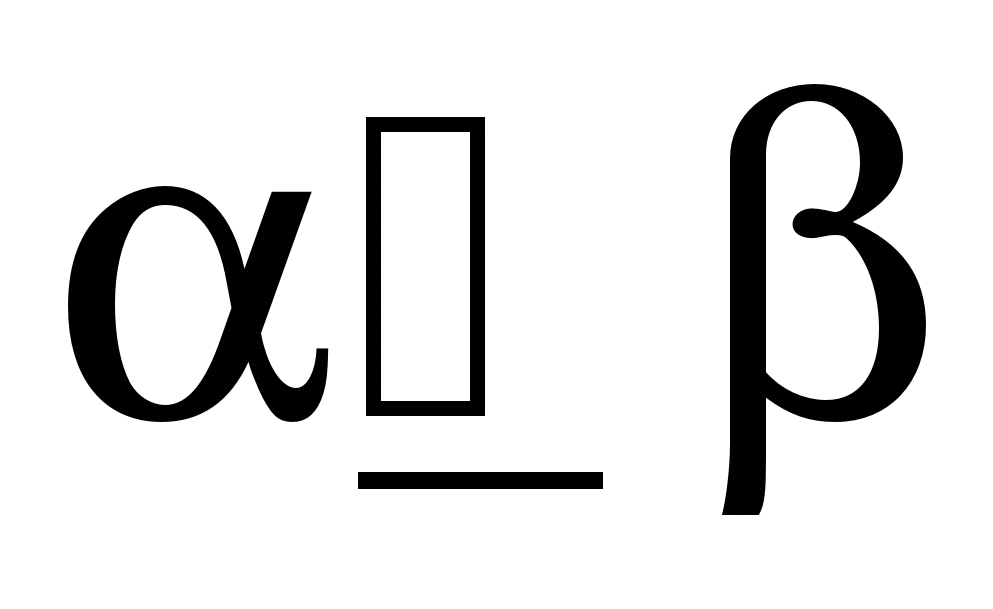), если .

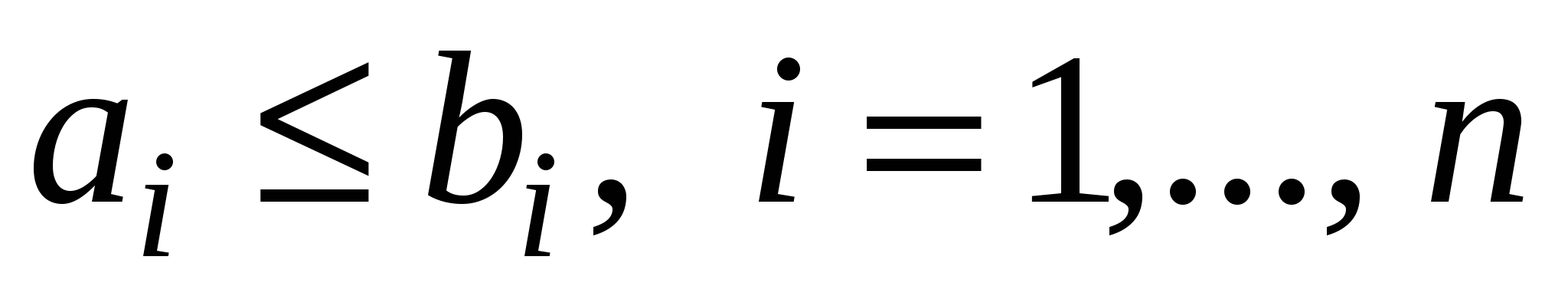функция 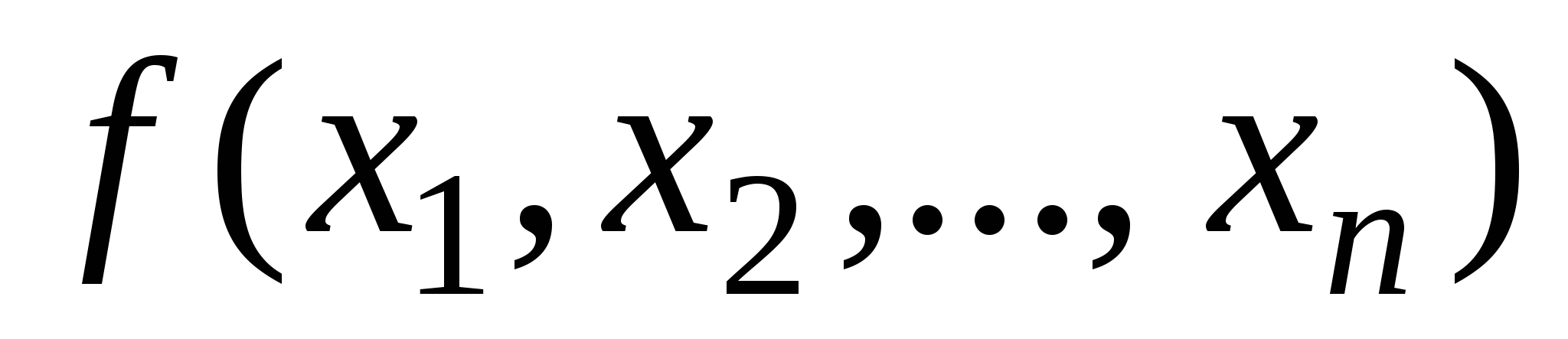монотонна, если для любых двух наборов таких, что они отвечают условиям , имеет место .

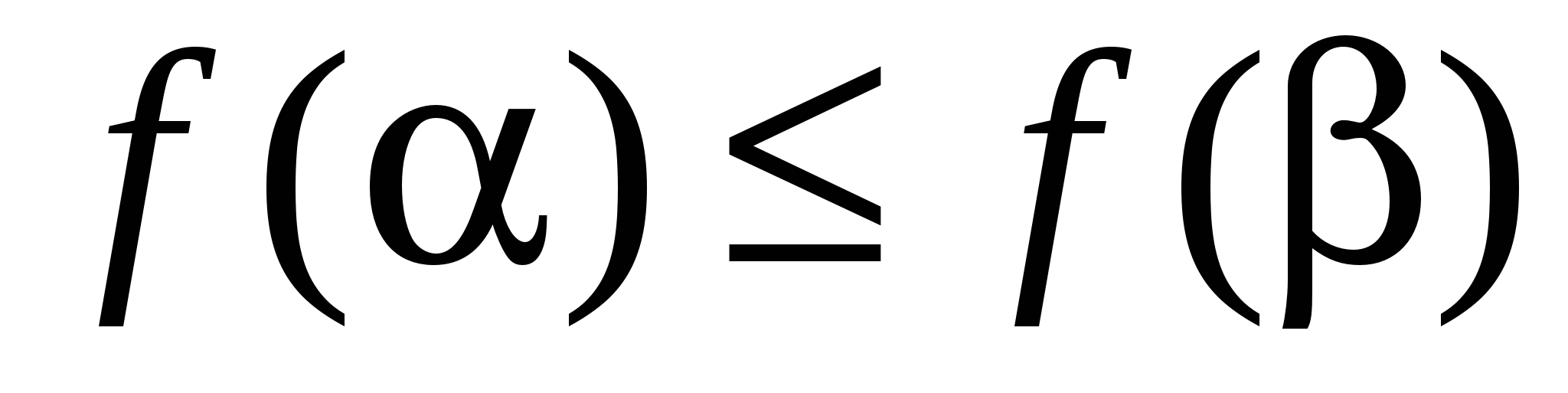Если хотя бы для одной пары таких наборов это не выполняется, то функция не монотонна. Например, функции 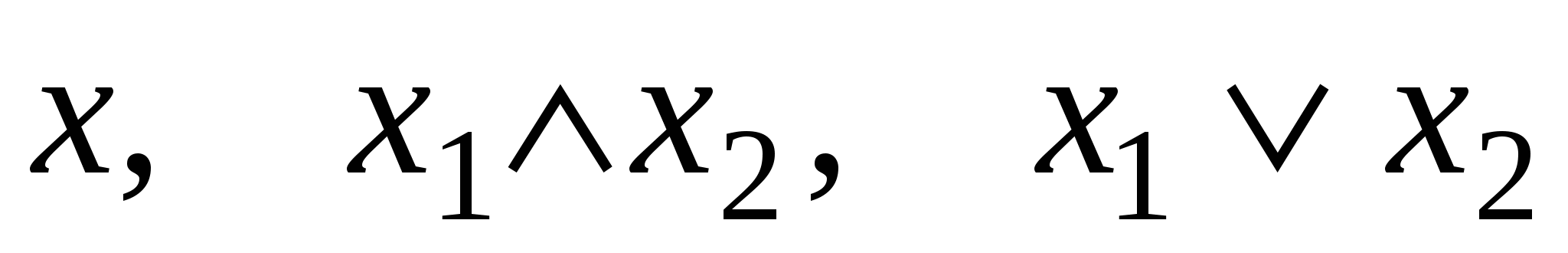монотонны, а функция 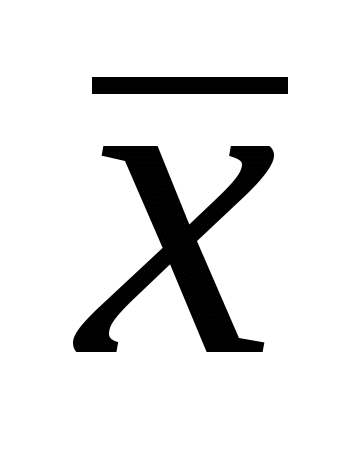не монотонна.

Замечание:Любая монотонная логическая функция может быть представлена в форме без инверсий.

Линейная функция

Функция называется линейной, если ее можно представить полиномом Жегалкина в виде суммы по модулю 2 константы a₀и переменныхx_i, умноженных на постоянные коэффициенты:

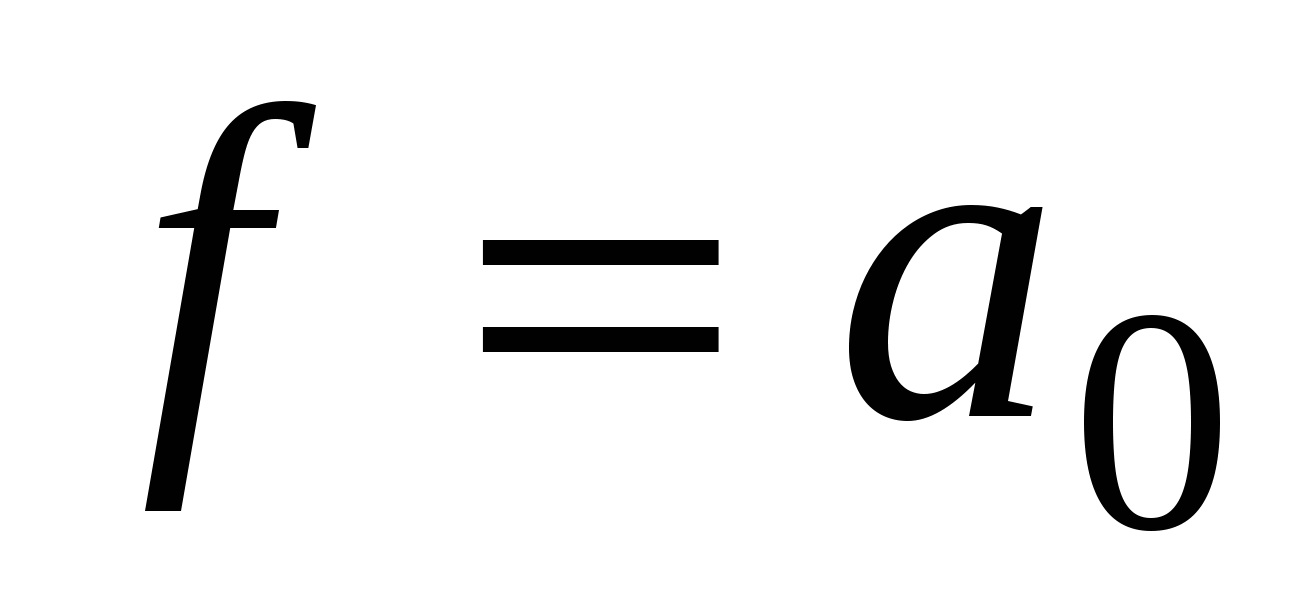
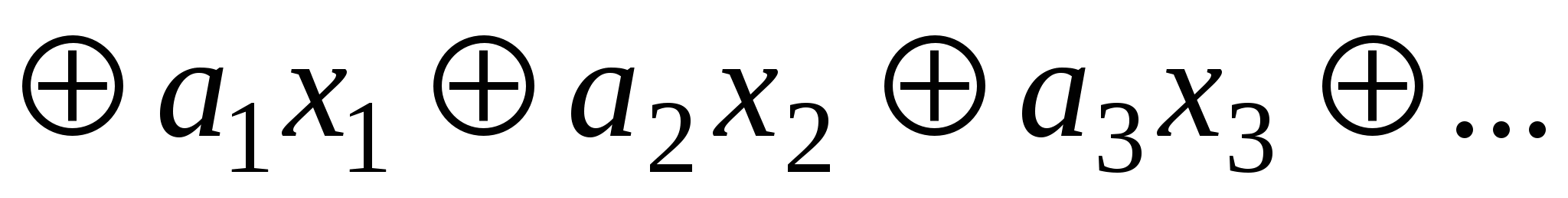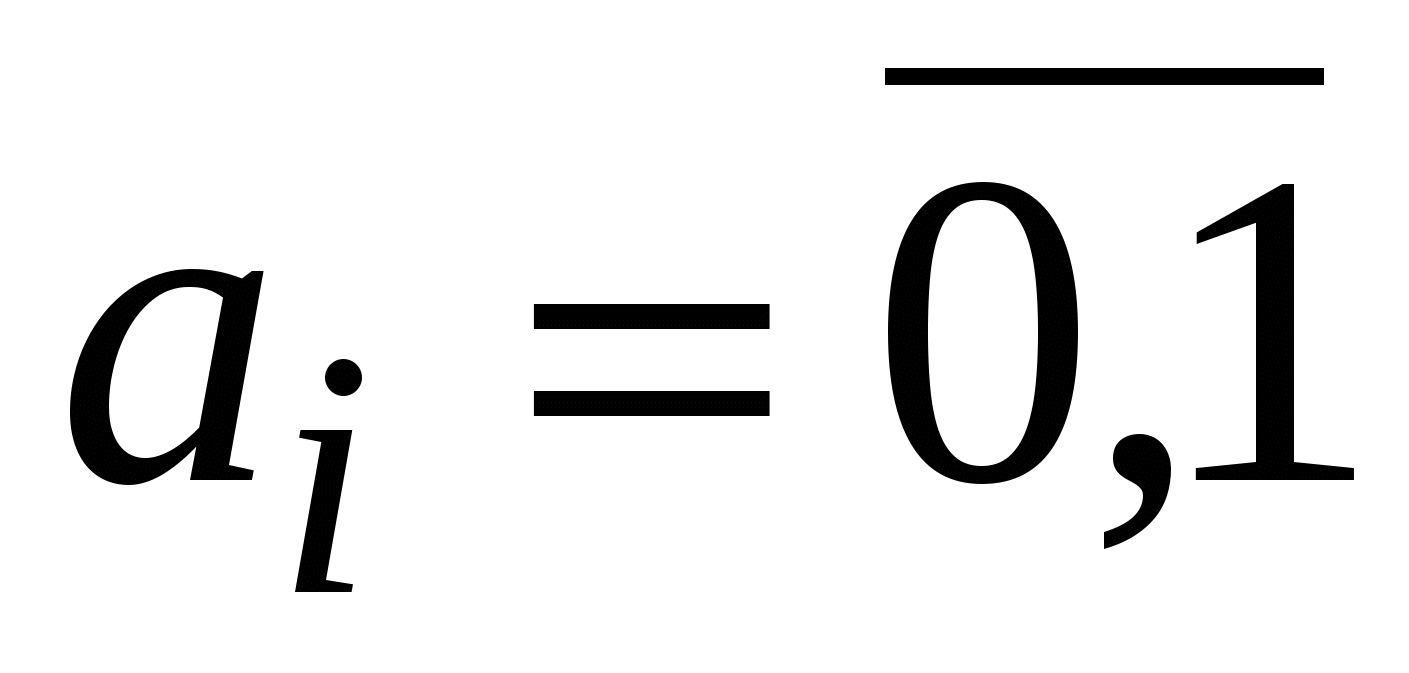, – линейная функция.

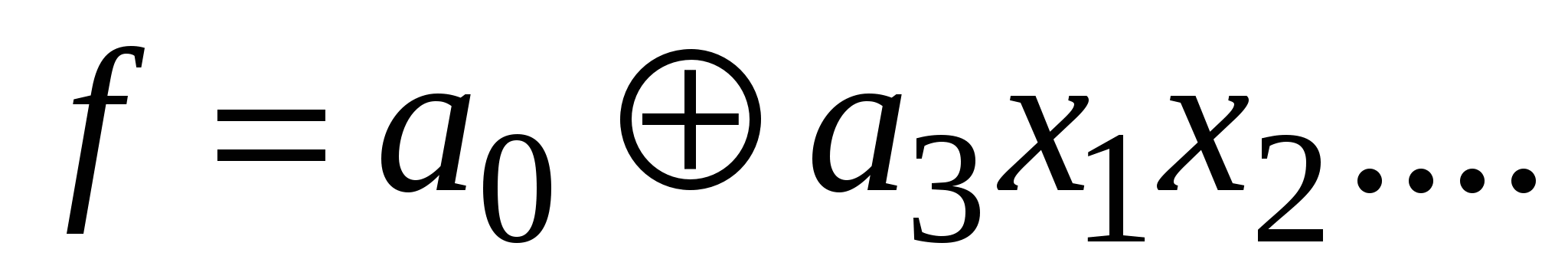– нелинейная функция, так как есть произведение переменных.

5. Понятие замкнутости систем логических функций. Замкнутость классов Т₀, Т_1, L, S, M.

Класс логических функций (множество логических функций) называется замкнутым, если любая суперпозиция функций этого класса снова будет функцией этого же класса. Основными замкнутыми классами логических функций являются классы линейных, самодвойственных, монотонных, сохраняющих константу 0 и 1 функций. Эти классы имеют специальные обозначения и обозначаются соответственно: L, S, M, T0, T1. При помощи основных замкнутых классов логических функций можно установить полноту систем логических функций,

Бинарные отношения

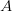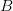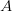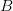Пусть и два конечных множества. Декартовым произведением множеств и называют множество 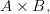состоящее из всех упорядоченных пар, где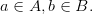

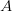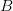Бинарным отношением между элементами множества и называется любое подмножество 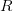множества 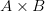, то есть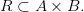

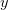По определению, бинарным отношением называется множество пар. Если R – бинарное отношение (т.е. множество пар), то говорят, что параметры и связаны бинарным отношением 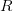, если пара 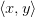является элементом R, т.е.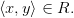

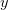Высказывание: “предметы и связаны бинарным отношением 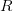” записывают в виде 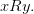Таким образом,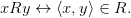

Если 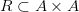, то говорят, что бинарное отношение определено на множестве .

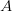Областью определения бинарного отношения 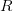называется множество, состоящее из таких , для которых 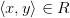хотя бы для одного .

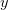Область определения бинарного отношения будем обозначать .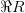

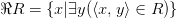
Областью значений бинарного отношения 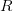называется множество, состоящее из таких 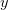, для которых 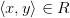хотя бы для одного .
Область значений бинарного отношения будем обозначать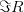

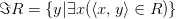
Инверсия (обратное отношение) 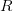— это множество и обозначается, как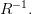

Композиция (суперпозиция) бинарных отношени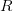й и 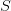— это множество 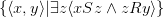и обозначается, как .

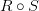Свойства бинарных отношений

Бинарное отношение 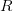на некотором множестве 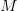может обладать различными свойствами, например:

· Рефлексивность: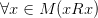

· Антирефлексивность (иррефлексивность):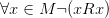

· Корефлексивность: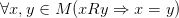

· Симметричность: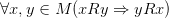

· Антисимметричность: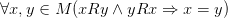

· Асимметричность: 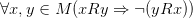. Асимметричность эквивалентна одновременнойантирефлексивности и антисимметричности отношения.

· Транзитивность: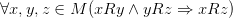

· Связность: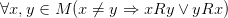

Задача о четырех красках.

Подмножества 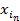множества х вершин, графа G(X) называется внутренне устойчивым, если вершины множества 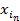не соединены ребрами. В противном случае неуст. Множество называется максимальным внутренне устойчивым, если оно становится внутренне неустойчивым при добавлении любой вершины.

Пример (x₁,x₃,x₅), (x₂,x₅) - внутр. уст.

(x₁,x₃,x₅) - максимальное внутрен.

уст. (x₁,x₃) - просто внутр. устр.

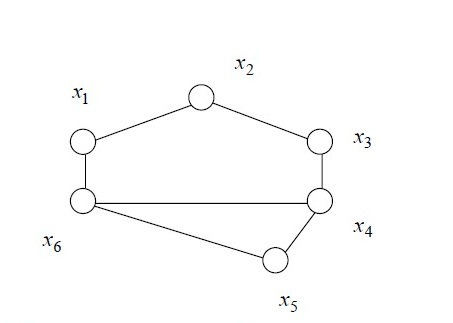
Любое внутреннее устойчивое множество вершин графа содержится в некотором максимальном внутр. устр. Максимальных несколько.

Числом внутренней устойчивости (G) графа G(X) называется

максимально число из чисел | 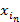|, 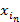- внутр. устро. множества, | 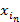| - число элементов множества 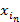, т.е. (G) = max | 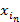|, 1≤ ≤n

Гипотеза четырех красок.

Достаточно ли четырех цветов для раскраски любой карты?

В 1890 году Хейвуд доказал, что достаточно пяти цветов.

Недавно американские математики Аппель и Хакон доказали гипотезу о четырех красках, существенно использовав ЭВМ. Таким образом для раскраски карты достаточно четырех красок. Для этого необходимо правильно подобрать внутренне устойчивые множества Вершин графа.

17. Задача Рамсея.

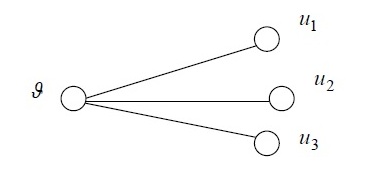
Доказать, что среди любых шести человек найдутся либо трое попарно незнакомых, либо трое попарно знакомых.

Отношение «быть знакомым» изобразим связывая вершин ребрам. Тогда три попарно знакомых образуют треугольник. В G – нет, Δ- ков, 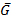- есть.

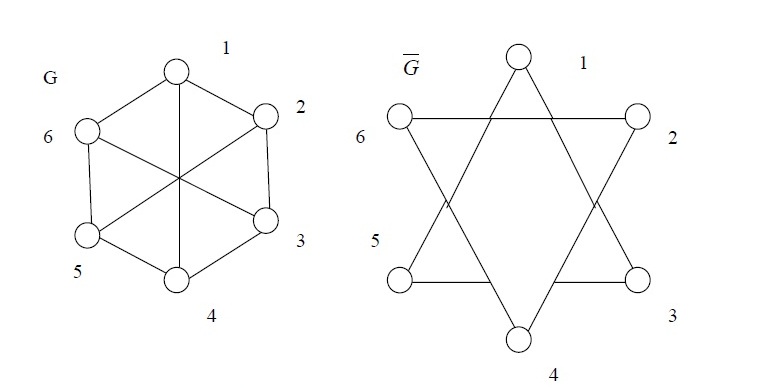
Доказательство. Пусть - произвольная вершина графа шестью вершинами.

Подберем три другие вершины графа G с которыми связан с ребром. Если нет таких и каждая вершина соединена только двумя другими вершинами, то такие вершины найдутся в 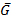и рассмотрим дополнение. Если при этом u1,u2,u3 не соед. ребром то они незнакомы, если есть хотя бы одно ребро то найдутся три знакомых. Теория доказана.

Элементы теории дискретных структур. Логические (булевы) функции. Теорема о числе логических функций от нескольких аргументов.

Булевой функцией от n аргументов называется функция 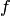, заданная на множестве 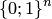и принимающая значения в двухэлементном множестве 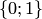. Другими словами, булева функция от 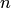аргументов сопоставляет каждому упорядоченному набору длины , составленному из элементов 0 и 1, либо 0, либо 1.

Булева функция от аргументов 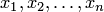обозначается так: .

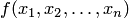Теорема о числе булевых функций. Число различных булевых функций, зависящих от n переменных, равно 2²ⁿ.

Доказательство. Каждая булева функция определяется своим столбцом значений. Столбец является булевым вектором длины m=2ⁿ, где n – число аргументов функции. Число различных векторов длины m (а значит и число булевых функций, зависящих от n переменных) равно 2^m=2²ⁿ.

2.Элементарные логические функции. Понятие формулы и эквивалентности формул. Основные равносильности. Разложение формул по переменным.

Среди булевых функций особо выделяются так называемые элементарные булевы функции, посредством которых можно описать любую булеву функцию от любого числа переменных.
1. Булева функция f(x₁, x₂ ... x_n) принимающая значение 1 на всех наборах нулей и единиц называется константой 1, или тождественной единицей. Обозначение: 1.
2. Булева функция f(x₁, x₂ ... x_n) принимающая значение 0 на всех наборах нулей и единиц называется константой 0, или тождественным нулем. Обозначение: 0.
3. Отрицанием называется булева функция одной переменной, которая определяется следующей таблицей истинности:

x
f(x)

Обозначения: x. Запись x читается «не икс» или «отрицание икс».
4. Конъюнкцией называется булева функция двух переменных, которая определяется следующей таблицей истинности:

x
y
f(x, y)

Другие названия: логическое умножение (произведение); логическое «и».
Обозначения: x&y, x⋅y, min(x,y).
Запись x&y может читаться так: «икс и игрек» или «икс умножить на игрек».
5. Дизъюнкцией называется булева функция двух переменных, которая определяется следующей таблицей истинности:

x
y
f(x, y)

Другие названия: логическое сложение (сумма); логическое «или».
Обозначения: x∨y, max(x,y).
Запись x∨y может читаться так: «икс или игрек» или «сумма икс и игрек».
6. Импликацией называется булева функция двух переменных, которая определяется следующей таблицей истинности:

x
y
f(x, y)

Другое название: логическое следование.
Обозначения: x→y, x⇒y, x⊃y.
Запись x→y может читаться так: «из икс следует игрек».
7. Эквивалентностью называется булева функция двух переменных, которая определяется следующей таблицей истинности:

x
y
f(x, y)

Обозначения: x∼y, x↔y.
Запись x∼y может читаться так: «икс эквивалентно игрек» или «икс равносильно игрек».
8. Cуммой по модулю 2 называется булева функция двух переменных, которая определяется следующей таблицей истинности:

x
y
f(x, y)

Другое название: антиэквивалентность.
Обозначения: x⊕y, x+y.
Запись x⊕y может читаться так: «икс плюс игрек».
9. Штрих Шеффера это булева функция двух переменных, которая определяется следующей таблицей истинности:

x
y
f(x, y)

Другое название: отрицание конъюнкции, логическое «не-и».
Обозначение: x|y.
Запись x|y может читаться так: «не икс или не игрек», «икс и игрек несовместны», «икс штрих Шеффера игрек».
10. Стрелка Пирса это булева функция двух переменных, которая определяется следующей таблицей истинности:

x
y
f(x, y)

Другое название: отрицание дизъюнкции, логическое «не-или», функция Вебба.
Обозначение: x↓y; для функции Вебба - x°y.
Запись x↓y может читаться так: «ни икс и ни игрек», «икс стрелка Пирса игрек».

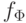Булевы формулы и называются эквивалентными, если соответствующие им функции и 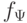равны.

Обозначение: . Эквивалентные формулы называют также тождественно равными, а выражения вида логическими тождествами.

Таким образом, эквивалентные формулы являются различными заданиями одной и той же булевой функции. Ниже мы приводим ряд парэквивалентных формул (тождеств), отражающих существенные свойства логических операций и важные соотношения между различными операциями. Они часто позволяют находить для булевых функций по одним задающим их формулам более простые формулы. Большинство из приводимых тождеств имеют собственные имена. Часто их называют законами логики.

Пусть - это одна из функций 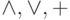. Для этих трех функций выполнены следующие две эквивалентности ( законы ассоциативностии коммутативности ).

1. Ассоциативность:

( 1)

2. Коммутативность:

( 2)

3. Дистрибутивные законы:

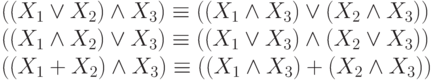( 3)

4. Двойное отрицание:

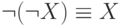( 4)

5. Законы де Моргана (внесение отрицания внутрь скобок):

( 5)

6. Законы упрощения:

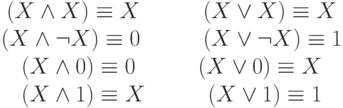( 6)

Некоторые законы упрощения имеют собственные названия: эквивалентности в первой строке называются законами идемпотентности, 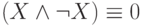- это закон противоречия, 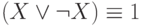- это закон исключенного третьего. Эквивалентности в двух последних строках иногда называют законами 0 и 1.

Следующие две эквивалентности позволяют выразить импликацию и сложение по модулю 2 через дизъюнкцию, конъюнкцию и отрицание.

	( 7)
	( 8)