Д.в. топольский, и.г. топольская
Д.В. Топольский, И.Г. Топольская
Арифметические и логические основы ЭВМ
ОГЛАВЛЕНИЕ
1. ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ.. 6
2. ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ.. 13
3. ВОСЬМЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ.. 15
4. ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ.. 17
5. ДВОИЧНО-ДЕСЯТИЧНЫЕ ЧИСЛА.. 19
6. ДВОИЧНАЯ АРИФМЕТИКА.. 20
7. АРИФМЕТИКА В ОБРАТНОМ И ДОПОЛНИТЕЛЬНОМ КОДАХ 22
8. МАТЕМАТИЧЕСКАЯ ЛОГИКА.. 25
ОТВЕТЫ К УПРАЖНЕНИЯМ.. 35
ПРЕДИСЛОВИЕ
Овладение базовыми знаниями в области компьютерных технологий является очень важной задачей для программистов. Глубокое понимание арифметических и логических основ ЭВМ позволяет создавать качественное программное обеспечению.
В пособии рассмотрены способы представления данных в памяти ЭВМ, их структура и правила преобразования. Каждый из восьми разделов пособия посвящен определенной теме, содержит теоретические сведения, примеры выполнения арифметических и логических операций, а также упражнения для практической и самостоятельной работы студентов.
Пособие предназначено для студентов очной и заочной формы обучения по специальности «Программное обеспечение вычислительной техники и автоматизированных систем».
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Рекомендуется следующая схема работы с пособием. После изучения необходимого материала на практическом занятии разбираются примеры выполнения арифметических и логических операций в ЭВМ. Каждой раздел содержит необходимый объем теоретических сведений и формулировку проблемы. Затем студентам может быть предложено выполнить находящиеся в конце раздела упражнения. Упражнения имеют различную сложность, которая нарастает с увеличением порядкового номера упражнения.
Для быстрого выполнения преобразований чисел из одной системы счисления в другую, помимо умения применять стандартные алгоритмы перевода, студенты должны помнить значения целых степеней числа 2 от 0 до 10, представление чисел от 0 до 16 в системах счисления с основаниями 2, 8, 10 и 16, а также знать свойства систем счисления с основаниями кратными 2.
При выполнении арифметических операций рекомендуется обозначать все заёмы и переносы из одного разряда в другой, имитируя тем самым работу регистра признаков. При работе с прямыми, дополнительными и обратными кодами рекомендуется использовать разрядность 8 бит.
При выполнении упражнений из раздела «Математическая логика» необходимо твердо усвоить символику и определения (таблицы истинности) трех основных логических операций. При вычислении значений логических выражений необходимо помнить приоритет выполнения логических операций.
В конце учебного пособия приводятся ответы к упражнениям.
ВВЕДЕНИЕ
Широкое внедрение вычислительной техники во все сферы человеческой деятельности, эффективность этого процесса неразрывно связаны как с развитием многочисленных сложных технических разработок, так и с уровнем подготовки в этой области специалистов самого разного профиля. Соответствие функциональных возможностей вычислительных систем и технологического назначения связанных с ними объектов обуславливает необходимость соответствующей подготовки программистов.
Решение этой задачи связано как с организацией учебного процесса на всех уровнях, включая и систему повышения квалификации специалистов, так и с его учебно-методическим обеспечением. Современные специалисты в области программного обеспечения должны обладать знаниями как об аппаратной, так и программной частях вычислительной техники.
Вычислительная техника развивается такими быстрыми темпами, что сейчас принято говорить о поколениях вычислительных машин, отличающихся элементной базой, характеристиками и назначением. Однако практически все вычислительные устройства имеют общие арифметические и логические основы, формы представления чисел, а также правила выполнения арифметических и логических операций. Именно эти вопросы рассматриваются в данном учебном пособии.
ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ
Любая информация представляется в ЭВМ с помощью цифровых знаков. Способ такого представления определяется принятой в ЭВМ системой счисления. Системой счисления называют совокупность приемов и правил наименования и обозначения чисел, с помощью которых можно установить взаимно однозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов. Всякая система счисления использует некоторый конечный алфавит, состоящий из цифр а1, а2, .... аn. При этом каждой цифре аi в записи числа соответствует определенный количественный эквивалент (ее «вес»).
Проанализируем «технологию» решения простой задачи — подсчета однородных предметов. Допустим, на столе лежат спички. Необходимо определить их количество и записать его: одна спичка — 1; еще одна спичка — 1; и т.д. Получим запись: 111111, где каждая спичка обозначена символом 1. Подсчитаем количество единиц (символов спичек) и запишем это количество в обычной (привычной) для нас форме — 6 или по-другому — VI. Итак, 6 = VI = 111111, т.е. количество спичек записано в различной форме. Форма записи 111111 очень громоздка; форма записи числа 6 наиболее удобна и привычна для нас.
В разные исторические периоды развития человечества для подсчетов и вычислений использовались те или иные системы счисления. Например, довольно широко была распространена двенадцатеричная система. Многие предметы (ножи, вилки, тарелки, носовые платки и т.д.) и сейчас считают дюжинами. Число месяцев в году — двенадцать.
Двенадцатеричная система счисления сохранилась в английской системе мер (например, 1 фут = 12 дюймов) и в денежной системе (1 шиллинг = 12 пенсов).
В древнем Вавилоне существовала весьма сложная шестидесятеричная система. Она, как и двенадцатеричная система, в какой-то степени сохранилась и до наших дней (например, в системе измерения времени: 1 ч = 60 мин, 1 мин = 60 с, аналогично в системе измерения углов: 1° = 60 мин, 1 мин = 60 с).
У некоторых африканских племен была распространена пятеричная система счисления, у ацтеков и народов майя, населявших в течение многих столетий обширные области американского континента, — двадцатеричная система. У некоторых племен Австралии и Полинезии встречалась двоичная система счисления.
Десятичная система измерения возникла в Индии. Впоследствии ее стали называть арабской потому, что она была перенесена в Европу арабами. Цифры, которыми мы теперь пользуемся, — арабские.
В разное время существовали другие записи цифр, в настоящее время почти забытые. Однако до сих пор мы иногда встречаемся с записью чисел с помощью букв латинского алфавита, например на циферблатах часов, в книгах для обозначения глав или частей, на деловых бумагах для обозначения месяцев и т.д.
Система счисления, в которой величина цифры определяется ее местоположением (позицией), называется позиционной. Таким образом, десятичная система счисления является позиционной. Римская система счисления не является позиционной, т.е. положение цифр не меняет ее значения. Например, число 9 запишем как IX, а число 11 — как XI. При этом знак I в обоих случаях имеет одно и то же значение — единица, только в одном случае он вычитается из десяти (X), а в другом случае — прибавляется. В ЭВМ используются только позиционные системы счисления. Число различных цифр системы счисления называется ее основанием S.
В общепринятой десятичной системе счисления используется десять различных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Позиции цифр в записи числа называют разрядами. В десятичной системе счисления мы имеем дело с разрядами единиц, десятков, сотен и т. д., а также с разрядами десятых, сотых, тысячных и т. д. долей единицы. Другими словами, в десятичной системе счисления «вес» каждого разряда в 10 раз больше «веса» предыдущего. Следовательно, всякое число в десятичной системе счисления образуется как сумма различных целых степеней десяти с соответствующими коэффициентами ai(0, 1, .... 9), взятыми из алфавита данной системы счисления. Таким образом, запишем десятичное число в общем виде:
А = а0×10n+а1×10n–1+а2×10n–2+…+аn–1×101+аn×100 = а0a1…an–1an.
Величина числа А определяется коэффициентами при степенях числа 10. Отсюда видно, что число 10 является основанием системы счисления, которая в данном случае называется десятичной. Например, десятичную запись 245,83 можно представить в виде:
245,83 = 2×102 + 4×101 + 5×100 + 8×10–1 + 3×10–2.
Опуская различные степени десяти, записывают только коэффициенты при этих степенях, т. е. 245,83. Аналогично:
531 = 5×102 + 3×101 + 1×100 = 531;
3527 = 3×103 + 5×102 + 2×101 + 7×100 = 3527;
28395 = 2×104 + 8×103 + 3×102 + 9×101 + 5×100 = 28395.
Для физического представления чисел в ЭВМ необходимы элементы, которые могут находиться в одном из нескольких устойчивых состояний. Число таких состояний должно равняться основанию принятой системы счисления. Тогда каждое состояние будет представлять соответствующую цифру из алфавита данной системы счисления. Наиболее простыми с точки зрения технической реализации являются так называемые двухпозиционные элементы, способные находиться в одном из двух устойчивых состояний — «включено» или «выключено». Например, электромагнитное реле замкнуто или разомкнуто, магнитный материал намагничен или размагничен, транзисторный ключ находится в проводящем или запертом состоянии и т.п. Одно из этих устойчивых состояний может представлять цифра 0, а другое — цифра 1.
Простота технической реализации двухпозиционных элементов обеспечила наибольшее распространение в ЭВМ двоичной системы счисления. Основание этой системы S = 2. В ней используются лишь две цифры: 0 и 1. Любое число в двоичной системе счисления представляется в виде суммы целых степеней ее основания S = 2, умноженных на коэффициенты; 0 или 1. Например, двоичное число
11011,012 = 1×24 + 1×23 + 0×22 + 1×21 +
+ 1×20 + 0×2–1 + 1×2-2 = 16 + 8 + 2 + 1 + 0,25 = 27,2510,
как это следует из приведенного разложения, соответствует десятичному числу 27,2510. Аналогично:
1210 = 1×23 + 1×22 + 0×21 + 0×20 = 11002;
4210 = 1×25 + 0×24 + 1×23 + 0×22 + 1×21 + 0×20 = 1010102.
Кроме двоичной в ЭВМ используются также восьмеричная и шестнадцатеричная системы счисления, которые применяются для более короткой и удобной записи двоичных кодов. Основания этих систем соответствуют целым степеням числа 2 (8 = 23; 16 = 24), поэтому для них исключительно просты правила перевода в двоичную систему счисления и наоборот.
В устройствах индикации широко применяется двоично-десятичный код. В таблице приведены коды систем счисления, из которой видно, что двоично-десятичный код отличается от десятичного тем, что в нем каждое число десятичного разряда записывается в двоичном коде.
В международной системе обозначений приведенные в таблице 1 коды обозначаются следующим образом: десятичный — DEC (decimal), двоичный — BIN (binary), восьмеричный — OCT (octal), шестнадцатеричный — HEX (hexadecimal), двоично-десятичный — BDC (binary-decimal code).
В ЭВМ применяются две формы представления чисел: с фиксированной запятой (точкой) и с плавающей запятой (точкой). Иначе эти формы соответственно называются естественной и полулогарифмической. Для названных форм представления чисел выделяется определенное количество nразрядов, образующих разрядную сетку ЭВМ. С увеличением n увеличиваются диапазон представляемых чисел и точность выполняемых расчетов.
При естественной форме число представляется в виде целой части числа и отделенной от нее точкой дробной части. Если, например, для целой и дробной частей числа отводится по три десятичных разряда, то число 245,6 будет представлено в виде: 245.600. Здесь точка, отделяющая целую часть числа от дробной, зафиксирована после третьего разряда.
Таблица 1
Представление чисел в различных системах счисления
| Десятичный | Двоичный | Восьмеричный | Шестнадцате-ричный | Двоично-десятичный |
| А | 0001 0000 | |||
| В | 0001 0001 | |||
| С | 0001 0010 | |||
| D | 0001 0011 | |||
| Е | 0001 0100 | |||
| F | 0001 0101 | |||
| 0001 0110 | ||||
| 0001 0111 | ||||
| 0001 1000 | ||||
| 0001 1001 | ||||
| 0010 0000 |
Обычно точку фиксируют справа от самого младшего разряда, и поэтому в такой форме могут быть представлены только целые числа. Используются два варианта представления целых чисел: без знака и со знаком. В первом случае все разряды служат для представления модуля числа. Во втором случае для представления знака числа выделяется крайний слева разряд, в котором записывается 0 для положительных чисел и 1 — для отрицательных.
Диапазон чисел, представленных с фиксированной точкой, ограниченный. Так, в n-разрядной сетке числа хбез знака могут быть представлены в диапазоне 0 £ x £ 2n -1. Для представления чисел, не укладывающихся в этот диапазон, в процессе программирования вводят соответствующие масштабные коэффициенты. Необходимость масштабирования данных — это существенный недостаток представления чисел с фиксированной точкой. Другой недостаток заключается в том, что при такой форме представления чисел относительная точность выполняемых расчетов зависит от значения чисел и достигает максимума при выполнении операций с максимально возможными числами.
В связи с этим представление чисел с фиксированной точкой является основной и единственной формой лишь для сравнительно небольших по своим вычислительным возможностям машин, например, в управляющих контроллерах. В ЭВМ, предназначенных для решения широкого круга задач, в основном используется представление чисел с плавающей точкой. Однако и в таких ЭВМ для целых чисел применяется форма представления с фиксированной точкой, поскольку операции с целыми числами выполняются в этой форме проще и за более короткое время.
В форме с плавающей точкой любое число Nпредставляется в виде произведения двух сомножителей: N = m×Sр, где m — мантисса числа (|m|)<1); р — порядок числа (целое число); S — основание системы счисления (целое число).
Например, десятичное число 6,15 в форме с плавающей точкой (запятой) можно записать следующим образом:
6,15 = 0.615×101;
6,15 = 0.0615×102;
6,15 = 0.00615×103 и т. д.
С изменением порядка в ту или иную сторону точка (запятая) как бы «плавает» в изображении числа. Таким образом, при представлении чисел с плавающей точкой в разрядной сетке ЭВМ необходимо записать со своими знаками мантиссу ±m и порядок ±р. Знак числа при этом совпадает со знаком мантиссы.
Для заданной разрядности мантиссы точность вычислений становится наибольшей, если мантисса представлена в нормализованном виде. Модуль нормализованной мантиссы должен удовлетворять условию (1/S) £ |m| < 1, при котором старший разряд мантиссы в S-ричной системе счисления не должен быть равен нулю. В процессе вычислений возможно нарушение нормализации вправо, когда |m| < (1/S), или влево, когда |m| ³ 1. В первом случае мантисса сдвигается влево до появления в старшем разряде ближайшей единицы. При этом в освобождающиеся младшие разряды мантиссы записываются нули и проводится соответствующее уменьшение порядка числа. При нарушении нормализации мантиссы влево производится ее сдвиг вправо с соответствующим увеличением порядка числа. Младшие разряды мантиссы, выходящие при этом за пределы разрядной сетки, отбрасываются.
ЭВМ обрабатывают не только числовую, но и различную алфавитно-цифровую информацию, содержащую помимо цифр буквенные, синтаксические, математические, различные управляющие и другие специальные символы. Такая информация представляется в ЭВМ двоичными кодами (двоичными словами) соответствующей разрядности.
ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Как уже отмечалось, в большинстве ЭВМ используется двоичная система счисления для представления и хранения различной информации, а также при выполнении арифметических и логических операций. В двоичной системе счисления основанием является число 2. В этом случае для записи чисел используют две цифры: 0 и 1.
Перевод числа из десятичной системы счисления в двоичную производится методом последовательного деления числа на 2 до тех пор, пока частное от деления не станет равным 1. Число в двоичной системе счисления записывается в виде остатков от деления, начиная с последнего частного, справа налево:
810 = 10002;
810 = 1×23 + 0×22 + 0×21 + 0×20;
810 = 8 + 0 + 0 + 0.
Перевод десятичного дробного числа в двоичную систему осуществляется в два этапа: вначале переводится целая часть числа (см. выше), затем дробная. Дробная часть переводится путем последовательного умножения дробной части на два. Двоичное число записывается в виде целых частей чисел, полученных при умножении только дробной части, начиная сверху после запятой. При этом задается точность выражений. Например, число 0,4110 в десятичной системе преобразуется в число 0,0112 в двоичной системе счисления:
| 0, | ||||
| ´ | ||||
| ´ | ||||
| ´ | ||||
| . |
По рассмотренным правилам числа можно переводить и в другие широко распространенные системы счисления — восьмеричную, шестнадцатеричную, двоично-десятичную. Во всех случаях умножение или деление переводимых чисел производится на основании новой системы счисления.
Упражнения
1. Преобразовать в десятичный код следующие двоичные числа:
а) 0001; б) 0101; в) 1000; г) 1011; д) 1111; е) 0111; ж) 10000000; з) 00010000; и) 00110011; к) 01100100; л) 00011111; м) 11111111.
2. Преобразовать в двоичный код следующие десятичные числа:
а) 23; б) 39; в) 55; г) 48.
3. Преобразовать десятичное число в двоичный код: 204;
4. Преобразовать двоичное число в десятичный код: 11101110.
Упражнения
1. Записать следующие восьмеричные числа в двоичном коде:
а) 3; б) 7; в) 0; г) 7642; д) 1036; е) 2105.
2. Записать следующие двоичные числа в восьмеричном коде:
а) 101; б) 110; в) 010; г) 111000101010; д) 1011000111; е) 100110100101.
3. Записать восьмеричное число в десятичном коде: 6724.
4. Записать десятичное число в восьмеричном коде: 2648.
Упражнения
1. Записать следующие шестнадцатеричные числа в двоичной форме:
а) C; б) 6; в) F; г) E2; д) 1A; е) 3D; ж) AO; з) 8B; и) 45; к) D7.
2. Преобразовать следующие двоичные числа в шестнадцатеричный код:
а) 1001; б) 1100; в) 1101; г) 1111; д) 10000000; е) 01111110; ж) 0010101; з) 11011011.
3. Преобразовать следующие шестнадцатеричные числа в десятичный код:
а) 7E; б) DB; в) 12A3; г) 34CF.
4. Преобразовать следующие десятичные числа в шестнадцатеричный код:
а) 217; б) 48373.
ДВОИЧНО-ДЕСЯТИЧНЫЕ ЧИСЛА
С целью удобства преобразования чистые двоичные числа представляются десятичными либо шестнадцатеричными. Однако двоично-десятичное преобразование — операция не простая. В контрольно-измерительной аппаратуре, устройствах индикации, телефонах, калькуляторах, когда на доступных пользователю выходах и входах широко распространены десятичные числа, для их представления используют специальный двоично-десятичный код.
Микропроцессоры выполняют арифметические операции с двоичными числами, но также они обладают командами для преобразования результата в двоично-десятичный код. Полученные двоично-десятичные числа легко затем представить в десятичной записи, использую табличный метод перекодировки с использованием таблицы.
Упражнения
1. Записать следующие десятичные числа в двоично-десятичном коде:
а) 99; б) 82; в) 17; г) 40; д) 65; е) 39.
2. Записать следующие двоично-десятичные числа в десятичном коде:
а) 01010101; б) 01000011; в) 01110110; г) 10010010; д) 00000001; е) 10000000.
ДВОИЧНАЯ АРИФМЕТИКА
Достоинством двоичной системы счисления, используемой в ЭВМ, является простота выполнения арифметических операций. Арифметические действия с двоичными числами выполняются по следующим правилам:
| сложение | вычитание | умножение |
| 0 + 0 = 0 | 0 – 0 = 0 | 0 ´ 0 = 0 |
| 0 + 1 = 1 | 1 – 0 = 1 | 0 ´ 1 = 0 |
| 1 + 0 = 1 | 1 – 1 = 0 | 1 ´ 0 = 0 |
| 1 + 1 = 0 + 1 переноса в старший разряд | 10 – 1 = 1 | 1 ´ 1 = 1 |
В случае многоразрядных двоичных чисел арифметические операции выполняются подобно тому, как это делается в десятичной системе счисления. Например, при сложении необходимо учитывать возможные переносы единицы из младших разрядов в старшие. При вычитании многоразрядных двоичных чисел может оказаться необходимым «занять» единицу в старшем разряде, что дает две единицы в младшем разряде. Умножение двоичных чисел сводится к умножению множимого на каждый разряд множителя, и последующему сдвигу множимого или множителя и суммированию образующихся частичных произведений. Деление двоичных чисел производится путем последовательного выполнения вычитаний и сдвигов. Например:
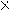 | |||||||||||||
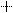 | |||||||||||||
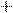 | |||||||||||||
Упражнения
1. Выполнить следующие сложения двоичных чисел:
а) 1010 + 0101; б) 1101 + 0101;
в) 01011011 + 00001111; г) 00111111 + 00011111.
2. Выполнить следующие вычитания двоичных чисел:
а) 1110 – 1000; б) 1010 – 0101;
в) 01100110 – 00011010; г) 01111000 – 00111111.
3. Выполнить следующие умножения двоичных чисел:
а) 1001 ´ 11; б) 1101 ´ 1001; в) 1111 ´ 101; г) 1110 ´ 1110.
Упражнения
Выполнить арифметические операции со следующими десятичными числами, используя метод дополнительного кода:
а) 7 + 1; б) 31 + 26; в) 8 – 5; г) 89 – 46; д) 1 – 6; е) 20 – 60;
ж) – 3 – 4; з) – 13 – 41; и) 7 – 2; к) 113 – 50; л) 3 – 8; м) 12 – 63.
МАТЕМАТИЧЕСКАЯ ЛОГИКА
Любая, даже самая примитивная ЭВМ — сложнейшее техническое устройство. Но даже такое сложное устройство, как и все в природе и в технике, состоит их простейших элементов. Все устройства ЭВМ состоят из десятков и сотен тысяч элементарных логических схем, так называемых вентилей, объединяемых по правилам и законам (аксиомам) алгебры логики в схемы и модули.
Автором алгебры логики является английский математик Джордж Буль. Занимаясь исследованием законов мышления, он применил в логике систему формальных обозначений и правил, близкую к математической. Впоследствии эту систему назвали логической алгеброй или булевой алгеброй. Правила этой системы применимы к самым разнообразным объектам и их группам (множествам, по терминологии автора). Основное назначение системы Буля состояло в том, чтобы кодировать логические высказывания и сводить структуры умозаключений к простым выражениям, близким по форме к математическим формулировкам. Результатом формального расчета логического выражения является одна из двух логических констант: истина или ложь.
Значение логической алгебры долгое время игнорировалось, поскольку ее приемы и методы не содержали практической пользы для науки и техники того времени. Однако, когда появилась принципиальная возможность создания средств вычислительной техники на электронной базе, операции введенные Булем, оказались весьма полезны. Они изначально ориентированы на работу только с двумя понятиями: истинности и ложности высказывания. Нетрудно понять, как они пригодились для работы с двоичным кодом, который в современных компьютерах тоже представляется всего двумя сигналами: 0 и 1.
Под высказыванием понимается повествовательное предложение, в котором что-либо утверждается или отрицается. В соответствии с такой двоичной природой высказываний условились называть их логическими двоичными переменными и обозначать «1» в случае истинности и «0» в случае ложности. Примерами логических переменных являются высказывания: X = «5 – это четное число», Y = «Квадрат – это геометрическая фигура». На основании этих высказываний можно записать X = 0, Y = 1, так как высказывание X ложно, а высказывание Y истинно.
Высказывания могут быть простыми и сложными: простые содержат одно законченное утверждение, сложные образуются из двух или большего числа простых высказываний, связанных между собой некоторыми логическими связями. Формализация и преобразование связей между логическими переменными осуществляются в соответствии с правилами алгебры логики.
Высказывания строятся над множеством {B, Ø, Ù, Ú, 0, 1}, где B — непустое множество, над элементами которого определены три операции: Ø — отрицание (НЕ), Ù — конъюнкция (И), Ú — дизъюнкция (ИЛИ), а также две константы — логический ноль 0 и логическая единица 1.
Отрицание (инверсия). В русском языке логической операции отрицание соответствует частица НЕ (в некоторых высказываниях применяется оборот «неверно, что…»). Отрицание — унарная (одноместная) операция. Записывается в виде: Ø X или 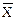 .
.
Конъюнкция (логическое умножение). В русском языке она выражается союзом И. В математической логике используются знаки Ù, & или ´. Конъюнкция — бинарная (двухместная) операция. Записывается в виде: X Ù Y, X & Y или X ´ Y. Значение такого выражения будет Ложь, если значение хотя бы одного из операндов ложно.
Дизъюнкция (логическое сложение). В русском языке она выражается союзом ИЛИ. В математической логике используются знаки Ú или +. Дизъюнкция — бинарная операция. Записывается в виде: X Ú Y или X + Y. Значение такого выражения будет Истина, если значение хотя бы одного из операндов истинно.
Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов: B = {0 (Ложь), 1 (Истина)}. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений, представленных в таблице, однако все они могут быть получены через суперпозицию трёх выбранных операций.
| Функции и их обозначение | Аргументы | Название функции | |||||
| X | Y | X | Y | X | Y | X | Y |
| f1 (XÙY) | Конъюнкция (логическое И) | ||||||
| f2 (XÚY) | Дизъюнкция (логическое ИЛИ) | ||||||
| f3 (XºY) | Эквивалентность | ||||||
| f4 (XÅY) | Сумма по модулю 2 | ||||||
| f5 (XÌY) | Импликация от y к x | ||||||
| f6 (XÉY) | Импликация от x к y | ||||||
| f7 (X¯Y) | Стрелка Пирса («антидизъюнкция») | ||||||
| f8 (X½Y) | Штрих Шеффера («антиконъюнкция») | ||||||
| f9 (XDY) | Инверсия импликации f5 | ||||||
| f10 (YDX) | Инверсия импликации f6 | ||||||
f11 ( 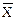 ) ) | Отрицание Х | ||||||
f12 ( 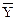 ) ) | Отрицание Y | ||||||
| f13 (X) | Переменная Х | ||||||
| f14 (Y) | Переменная Y | ||||||
| f15 (1) | Константа 1 | ||||||
| f16 (0) | Константа 0 |
Логическая функция (логическое выражение) — формула, содержащая только логические величины и знаки логических операций. Результатом вычисления логической функции является Истина или Ложь.
Не вся система Буля (как и не все предложенные им логические операции) были использованы при создании электронных вычислительных машин. Наибольший практический интерес представляют функции отрицания, логического умножения и логического сложения.
Логическое отрицание НЕ переменной X есть логическая функция F, которая истинна только тогда, когда переменная X имеет значение Ложь, и наоборот.
В алгебре логики любые функции удобно изображать в виде таблицы соответствия всех возможных комбинаций входных логических переменных и выходной логической функции. Для функции логического отрицания НЕ эта таблица имеет вид:
| X | F |
Графически эта функция обозначается кружком на входе или выходе логического символа (рис. 1).
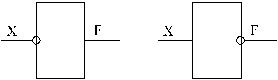
Рис. 1. Графическое изображение функции логического отрицания НЕ
Логическое умножение И двух переменных X и Y есть логическая функция F, которая истинна тогда и только тогда, когда одновременно истинны входные переменные. Для функции логического умножения И таблица истинности имеет вид:
| X | Y | F |
Графическое изображение функции логического умножения И представлено на рис. 2.
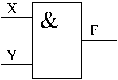
Рис. 2. Графическое изображение функции И
Логическое сложение ИЛИ двух переменных X и Y есть логическая функция F, которая истинна, когда хотя бы одна из входных переменных истинна. Для функции логического сложения ИЛИ таблица соответствия имеет вид:
| X | Y | F |
На рис. 3 представлено графическое изображение функции логического сложения ИЛИ.
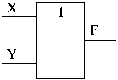
Рис. 3. Условно-графическое изображение функции логической суммы
Три рассмотренные функции позволяют реализовать любую логическую зависимость, они лежат в основе базовых схемотехнических элементов.
Базисом называется совокупность элементов, с помощью которых схемотехнически можно реализовать устройство любой сложности. То есть, базис — это те элементы, при помощи которых можно сделать любое устройство (речь идет о цифровой технике). Из указанных простейших базовых логических элементов собирают, конструируют сложные логические схемы ЭВМ. Например, сумматоры, шифраторы, дешифраторы и др. Большие интегральные схемы (БИС) и сверхбольшие (СБИС) интегральные схемы также содержат в своем составе (на кристалле кремния площадью в несколько квадратных сантиметров) десятки тысяч вентилей.
Это возможно еще и потому, что базовый набор логических схем (инвертор, конъюнктор, дизъюнктор) является функционально полным (любую логическую функцию можно представить через эти базовые вентили), представление логических констант в них одинаково (одинаковы электрические сигналы, представляющие 1 и 0) и различные схемы можно «соединять» и «вкладывать» друг в друга (осуществлять композицию и суперпозицию схем). На их основе можно сделать все вышеперечисленные элементы. Таким способом конструируются более сложные узлы ЭВМ — ячейки памяти, регистры, шифраторы, дешифраторы, а также сложнейшие интегральные схемы.
Кроме того, широкое распространение получили в реализации современных логических схем функции И-НЕ, ИЛИ-НЕ, исключающее ИЛИ.
«И-НЕ» — это схема И и схема НЕ, сложенные вместе. Операция, которую производит такой элемент, называется инверсией логического умножения или отрицанием логического умножения, или инверсией конъюнкции, а также штрих Шеффера. В виде формулы операция И-НЕ записывается так: F = X | Y.
Таблица истинности для этой функции представлена в следующем виде:
| X | Y | F |
Графическое изображение функции И-НЕ представлено на рис. 4.
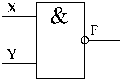
Рис. 4. Графическое представление функции И-НЕ
Операция, выполняемая элементом ИЛИ-НЕ, называется инверсией логического сложения или инверсией дизъюнкции и еще словосочетанием «стрелка Пирса». В виде формулы эта функция записывается так: F = X↓Y.
Значения этой функции при различных X и Y могут быть представлены в таблице истинности:
| X | Y | F |
