Глава 1. логика высказываний
Глава 1. Логика высказываний
Основные понятия

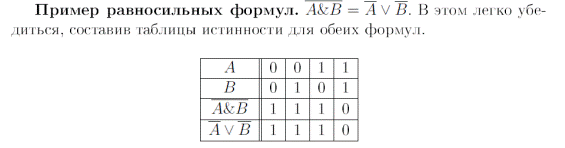
Истинностные значения «истина» и «ложь» будем обозначать прописными буквами И и Л соответственно.
Высказывание называется простым (элементарным), если оно рассматривается как некое неделимое целое. Сложным (составным) называется высказывание, составленное из простых с помощью логических связок (операций).
Основными логическими операциями над высказываниями являются: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность, неравнозначность.
Отрицанием (инверсией) высказывания P называется высказывание, истинное тогда и только тогда, когда высказывание P ложно, и ложное в противном случае. Обозначения: 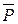 , ù P. Читается: «не P». Отрицание определяется таблицей истинности (табл. 4.1).
, ù P. Читается: «не P». Отрицание определяется таблицей истинности (табл. 4.1).
Конъюнкцией (операцией «И», логическим произведением) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания, и ложное во всех других случаях. Обозначения: P&Q, P×Q, PÙQ. Читается: «P и Q». Конъюнкция определяется таблицей истинности (табл. 4.2).
Дизъюнкцией (операцией «ИЛИ», логической суммой) двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны, и истинное – во всех других случаях. Обозначения: PÚQ, P+Q. Читается: «P или Q» (понимается как неразделительное «или»). Дизъюнкция определяется таблицей истинности (табл. 4.3).
Импликацией (логическим следованием) двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда P истинно, а Q ложно, и истинное – во всех других случаях. Обозначения: P®Q, PÉQ. Читается: «если P, то Q», «P влечет Q»). Высказывание P называется посылкой импликации, а высказывание Q - заключением. Импликация определяется таблицей истинности (табл. 4.4).
Эквивалентностью (равнозначностью, эквиваленцией) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинностные значения P и Q совпадают, и ложное в противном случае. Обозначения: P«Q, P~Q, PºQ. Читается: «P эквивалентно Q», «P, если и только если Q», «P равнозначно Q». Эквивалентность определяется таблицей истинности (табл. 4.5).
Неравнозначностью (исключающим «ИЛИ», сложением по модулю 2) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинностные значения P и Q не совпадают, и ложное – в противном случае. Обозначения: PÅQ, PDQ. Читается: «P неравнозначно Q», «либо P, либо Q», «или P, или Q» (понимается – в разделительном смысле). Неравнозначность определяется таблицей истинности (табл. 4.6).
Буквы, обозначающие высказывания, логические связки и скобки, составляют алфавит языков логики высказываний: алгебры логики и исчисления высказываний.
Логической формулой называется выражение, составленное из обозначений высказываний, логических операций и скобок, и удовлетворяющее следующим условиям:
- любая переменная, обозначающая высказывание, - формула;
- если P и Q – формулы, то 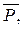 P&Q, PÚQ, P®Q, P«Q, PÅQ – формулы;
P&Q, PÚQ, P®Q, P«Q, PÅQ – формулы;
- других формул нет.
Пример 4.1. Представить логическими формулами следующие высказывания:
1. «Сегодня понедельник или вторник».
2. «Идет дождь или снег».
3. «Если идет дождь, то крыши мокрые. Дождя нет, а крыши мокрые».
4. «Что в лоб, что по лбу».
Решение.
1. Составное (сложное) высказывание «Сегодня понедельник или вторник» состоит из двух простых:
P – «Сегодня понедельник»; Q – «Сегодня вторник».
Высказывания P и Q соединены связкой «или» в разделительном смысле. Поэтому данное высказывание представимо логической формулой:PÅQ.
2. Составное высказывание «Идет дождь или снег» состоит из двух простых:
P – «Идет дождь»; Q – «Идет снег».
Высказывания P и Q соединены связкой «или» не в разделительном, а в обычном смысле. Таким образом, логическая формула имеет вид:P Ú Q.
3. Первое предложение «Если идет дождь, то крыши мокрые» включает два простых высказывания:
P – «Идет дождь»; Q – «Крыши мокрые».
Высказывания P и Q соединены связкой «если ¼ , то ¼»:P ® Q.
Второе предложение «Дождя нет, а крыши мокрые» также как и первое включает высказывания:
P – «Идет дождь»; Q – «Крыши мокрые».
Союз “а” имеет смысл связки «и», кроме того высказывание P используется с отрицанием, т.е. второе предложение представляется в виде: 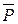 & Q.
& Q.
Далее, объединяем оба предложения в одно высказывание связкой &:(P ® Q) &( 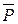 & Q).
& Q).
4. Составное высказывание «Что в лоб, что по лбу» состоит из двух простых:
P – «В лоб»; Q – «По лбу».
Высказывания P и Q соединены связкой «равнозначно»:P « Q.
Алгебра логики








Предикаты








Множества
Множество относится кпервоначальным понятиям науки, не определяемым через другие, более простые термины. Множество представляет собой определенную совокупность объектов, объединенных в единое целое в соответствии с некоторыми признаками и правилами.Множества обозначаются: A, B, C, X, Y, Z. Примеры множеств:
· множество всех атомов на Марсе;
· множество точек окружности;
· множество решений заданного уравнения;
· множество всех действительных чисел - R.
Г. Кантор (1845–1918 гг.) определял Множество как «многое, понимаемое как единое».
Наконец, определение Множества как «совокупности определенных различаемых объектов». Здесь для «объекта» важен просто сам факт принадлежностик Множеству – своеобразное характеристическое свойство.
Таким образом, в общем случае требуется задать характеристическое свойство, которым должны обладать все элементы множества. Способ задания «принадлежности», или попросту, путем перечисления годится, только для конечныхмножеств.
Множества обозначаются обычно большими латинскими буквами (необязательно), в их определении используется фигурные скобки ( {} ). Например, M = {a, b, c }.
Здесь определено 3-элементное множество путем простого перечисления элементов.
Еще пример, множество натуральных чисел: N= {1, 2, 3, …}.
Это бесконечное множество (о других его определениях еще придется говорить).
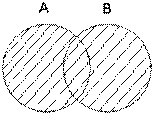
Рис. 1. Диаграмма Венна
Для пересечения множеств
Объединение множеств(рис. 2): А È В = {х : х Î А или х Î В}.
 «È» похоже на незавершенную русскую букву «О» («объединение»). ИЛИ здесь – не исключительное, т. е. это аналог «обычной» нестрогойдизъюнкции. Есть еще строгая дизъюнкция (ИЛИ-ИЛИ), в логике она обозначается «
«È» похоже на незавершенную русскую букву «О» («объединение»). ИЛИ здесь – не исключительное, т. е. это аналог «обычной» нестрогойдизъюнкции. Есть еще строгая дизъюнкция (ИЛИ-ИЛИ), в логике она обозначается « 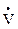 ».
».
Рис. 2. Объединение множеств
Утверждение: Для любых множеств А и В мощность объединения
çА 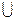 Вç=çАç+çВç-çА
Вç=çАç+çВç-çА 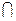 Вç
Вç
Первые две операции фактически обладают теми же свойствами, что и операции &, v в алгебре логики.
Например, они коммутативны: А * В = В * А, и это, вообще-то, свойство логических связок «и», «или».
Они идемпотентны: А * А = А.
Свойство идемпотентности позволяет произвольно сжимать или расширять выражения, что весьма полезно в разного рода преобразованиях.
Кстати, {1, 2} Ç {2, 3} = {2},
{1, 2} È {2, 3} = {1, 2, 3},
но
 {{1, 2}, {2, 3}} ¹ {1, 2 , 3}!
{{1, 2}, {2, 3}} ¹ {1, 2 , 3}!
Разностьдвух множеств А \ В = {х : х Î А и х Ï В}. (рис. 3):
Рис. 3. Разность двух множеств
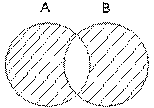 Заштрихованная область на рис. 3 соответствует дополнению В до А. Аналогично можно определить разность В \ А, или дополнение А до В (область В на рис. 3 без общей части).
Заштрихованная область на рис. 3 соответствует дополнению В до А. Аналогично можно определить разность В \ А, или дополнение А до В (область В на рис. 3 без общей части).
Симметрическая разность (рис. 4): А D В = (А È В) \ (А Ç В).
Рис. 4. Симметрическая разность
Как видно, здесь реализуется исключительное ИЛИ (строгая дизъюнкция). В алгебре логике существует аналог: А Å В = (А v В) 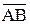 .
.
Действительно, (А v В) 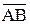 = (А v В) (`А v `В ) = А`В v `АВ = А Å В.
= (А v В) (`А v `В ) = А`В v `АВ = А Å В.
Дополнение множества (до универсального): А¢ = Е \ А = {х : х Ï А}.
Множество и его дополнение однозначно определяются двумя равенствами (используются в доказательствах):
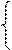 А Ç А¢ = Æ,
А Ç А¢ = Æ,
А È А¢ = Е.
Рис. 6. Диаграмма Венна
Элементы комбинаторики
Принцип сложения
Если выбор А можно осуществить n способами, а выбор В можно осуществить m способами, то выбор либо А, либо В можно осуществить m+n способами, в случае если при выборе способов нет совпадений, если k – число совпадений, то выбор либо А либо В можно осуществить m+n-k способами.
Принцип умножения
Пусть выбор А можно осуществить n способами, а выбор В - m способами, тогда выбор А и В можно осуществить m*n способами.
Решим задачу.
1.Из Ростова-на-Дону до Москвы можно добраться пароходом, поездом, автобусом и самолетом. Из Москвы до Санкт-Петербурга поездом, автобусом и самолетом. Сколькими способами можно осуществить путь по маршруту Ростова-на-Дону – Москва - Санкт-Петербург.
| Ростова-на-Дону | пароходом | Москва | поездом | Санкт-Петербург |
| поездом | автобусом | |||
| автобусом | самолетом | |||
| самолетом |
4*3=12
Выбор А*В можно осуществить 12 способами.
2.В стране чудес есть 4 города А, В, С, Д. Из города А в город В ведет 6 дорог, из В в Д – 4, из А в С – 2, из С в Д – 3. Сколькими способами можно проехать от А до Д.
| А | В | |
| С | Д |
2*3+6*4=30
Соединения без повторений
| Соединение предметов | ||
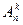 | 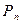 | 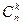 |
| Размещение из n элементов по k элементам (важен порядок и важны сами элементы) | Перестановка n элементов без повторения (важен порядок, элементы не важны) | Сочетание из n элементов по k элементам (важны элементы, порядок не важен) |
Определение: Введем множество N0=NÈ{0}.Пусть элементы k, n ÎN0, причем k£n. Размещением из n элементов множества В={b1, b2,…, bn} по k элементам будем называть всякую последовательность, составленную из неповторяющихся элементов множества В, имеющую длину k
(а1, а2, …, аk).
Пример: А={1,2,3}. Выпишем все размещения из трех элементов по 2
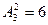 (1,2); (1,3); (2,1); (2,3); (3,1); (3,2)
(1,2); (1,3); (2,1); (2,3); (3,1); (3,2)
ТеоремаПусть дано множество В={b1, b2,…, bn} k, n ÎN0, k£n. Число размещений из n элементов по k элементам без повторений можно вычислить по формуле:
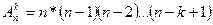 =
= 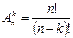
Для доказательства воспользуемся принципом умножения. Для построения каждого размещения нужно рассмотреть последовательность из n элементов. На первом месте n возможностей, на втором n-1.
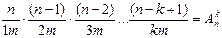
Пусть (n-k)!=1*2*3*…(n-k) n!=1*2*3*…*(n-k)*(n- k +1)*…*n
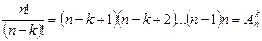
Определение: Пусть N0=NÈ{0}, k, n ÎN0, k£n, В={b1, b2,…, bn}. Сочетаниемиз n элементов по k элементам без повторений будем называть всякое подмножество множества В, состоящее из k неповторяющихся элементов заданного множества В.
Пример: А={0,1,4}. Выпишем все размещения из трех элементов по 2
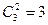 {0,1}; {1,4};{ 0,4}
{0,1}; {1,4};{ 0,4}
ТеоремаПусть k, n ÎN0, k£n, В={b1, b2,…, bn}. Число сочетаний из n элементов по k элементам можно подсчитать используя формулу: 
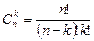
Рассмотрим формулу из предыдущей теоремы. Число размещений равно 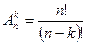 . Ясно, что число размещений
. Ясно, что число размещений 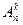 можно связать с числом сочетаний формулой
можно связать с числом сочетаний формулой 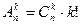 .
. 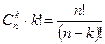 следовательно
следовательно 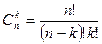 .
.
Задача: Сколькими способами можно рассадить 4 учащихся на 25 местах.
I способ (принцип умножения)
25*24*23*22=303600
II способ (размещение)
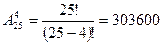
Задача: Учащемуся необходимо сдать 4 экзамена на протяжении 8 дней. Сколько способов? Решить задачу если известно, что последний экзамен будет сдаваться на 8 день.
1) 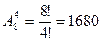
2) 4* 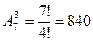
Задача: Сколькими способами читатель может выбрать 3 книги из 5.
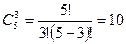
Задача: В турнире принимали участие n шахматистов, каждые два шахматиста встретились 1 раз. Сколько партий было в турнире?
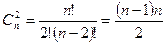
Определение: Пусть n ÎN0, В={b1, b2,…, bn}. Перестановкой n элементов множества В будем называть всякое размещение без повторений из n элементов по n элементам.
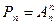
Теорема 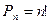 . Число перестановок n элементов множества равно n! n ÎN0, В={b1, b2,…, bn}.
. Число перестановок n элементов множества равно n! n ÎN0, В={b1, b2,…, bn}.
Пусть 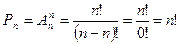
Следствие: n, k ÎN0, k£n, В={b1, b2,…, bn}. Число размещений из n элементов по k элементам модно вычислить по формуле:
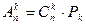
Задача: Сколькими способами можно разместить в очередь 7 человек.
N=7 Р7=7!
Задача: Сколькими способами можно упорядочить множество 1, 2, 3, …, 2n, так чтобы каждое четное число имело четный номер.
А={1, 2, 3, …, 2n} n!*n!=(n!)2.
Задача: Сколько можно составить перестановок из n элементов, в которых данные два элемента не стоят рядом.
n!-(n-1)!2!=(n-1)!(n-2)
Свойства сочетаний
1° 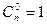 2°
2° 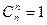 3°
3° 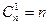
4° 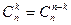 5°
5° 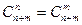 6°
6° 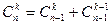 7°
7° 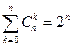 ( из7)
( из7)
Из св 6 можно последовательно находить 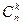 зная
зная 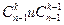 . в виде треугольника Паскаля:
. в виде треугольника Паскаля:
Формула бинома Ньютона
(а+b)n= 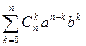 (можно доказать по индукции)
(можно доказать по индукции)
Перемножим (а+b) само на себя n раз, получим сумму, содержащую 2n слагаемых, каждое слагаемое представляет произведение d1*d2*…*dn, где di либо а, либо b, 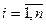 , полученную сумму разобьем на n+1 слагаемых В0, В1, …Вn.
, полученную сумму разобьем на n+1 слагаемых В0, В1, …Вn.
Пусть у нас в группе Вk содержатся те произведения, в которых элемент b встречается k раз, а элемент a встречается (n-k) раз.
Полиномиальная теорема
(а1+а2+…+аk)n= 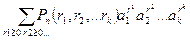
Перемножим сумму k слагаемых на себя n раз
(а1+а2+…+аk)… (а1+а2+…+аk), получим kn слагаемых вида d1d2…dn, где каждый множитель di равен либо а1,а2,…,аk. Обозначим В(r1, r2, …,rk) совокупность всех тех слагаемых, в которых элемент а1 встречается r1 раз, а2 встречается r2 раза, аk встречается rk раз. Число таких слагаемых равно 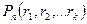
Пусть элемент а повторяется r раз, элемент b – (n-r) раз соответственно, полиномиальный коэффициент
Рn(r,n-r)= 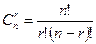
Упражнение: Покажите, что 
Отношения. Основные понятия
Отношения – это один из способов задания взаимосвязей между элементами множества. Наиболее распространены унарные и бинарные отношения.
Унарные (одноместные) отношения отражают наличие какого-либо определенного признака R у элементов множества A.
Все элементы множества A, обладающие признаком R, образуют некоторое подмножество: AR = ía: aÎA & aÎRý.
Бинарные (двухместные) отношения используются для определения взаимосвязей, которыми характеризуются пары элементов множества A. Например, на множестве людей могут быть заданы следующие бинарные отношения: «жить в одном городе», «учиться в одном институте».
В общем случае отношения могут быть n-местными. Под n-местным отношением понимают подмножество R прямого произведения n множеств:
RÍM1´M2´¼´Mn.
Бинарным отношением R называется подмножество пар (a,b) Î R декартового произведения M1´M2, где R Í M1´M2. Множество M1 – область определения отношения R, множество M2 – область значений отношения R.
Если задано отношение R между парами элементов одного и того же множества M, то R Í M´M.
Вместо записи (a,b) Î R используют также обозначение a R b.
Шахматная доска доставляет пример бинарного отношения на множестве горизонталей G = {1, 2, …, 8} и множестве вертикалей W = {a, b, …, h}. В результате получается множество клеток доски: D = W * G = {(a, 1), (a, 2), …, (h, 8)}, |D| =64.
Выделяются три отношения:
– пустое отношение, Æ Í М2;
– универсальное отношение, UM = {(x, y): x, y Î M};
– тождественное отношение, IM = {(x, x): x ÎM}.
Область D(R) определения и область значений Q(R) отношения R определяются в виде:
D(R) = ía: (a,b)ÎRý, Q(R) = íb: (a,b)ÎRý.
Задать бинарные отношения можно любым способом задания множеств:
1) В виде характеристического свойства R = í(a,b): (a,b)ÎRý, где в правой части равенства вместо R записывается характеристическое свойство.
2) Списком (перечислением) пар, для которых выполняется данное отношение. Например, R = í(a,b), (a,d), (b,c)ý.
3) Матрицей. Отношению R Í M´M, где M = ía1, a2, ¼, aný, соответствует квадратная матрица порядка n, в которой элемент cij, стоящий на пересечении i-й строки и j-го столбца, равен 1, если между ai и aj имеет место отношение R, или 0, если оно отсутствует:
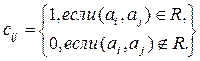 .
.
Пример 2.1. Пусть M = í1, 2, 3, 4, 5ý. Задать в виде характеристического свойства, списком (в явном виде) и матрицей отношение R Í M´M, если R означает «быть меньше».
Решение. Отношение R как множество содержит все пары элементов a,b из M, такие что a<b. Тогда отношение R в виде характеристического свойства имеет вид:
R = í(a,b): a<b, a,bÎMý.
В виде списка отношение R выглядит следующим образом:
R = í(1,2), (1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,4), (3,5), (4,5)ý.
Матрица отношения R приведена на рис. 2.2.

Можно рассмотреть несколько вариантов графического представления отношений:
 – точки в плоскости D
– точки в плоскости D  F;
F;
– ориентированные отрезки (со стрелками)
 от точек оси абсцисс, соответствующих левым
от точек оси абсцисс, соответствующих левым
элементам пар, к точкам оси ординат,
 соответствующих правым элементам;
соответствующих правым элементам;
– двудольный орграф
(левая доля соответствует области определения
D, правая – области значений F);
– ориентированный граф порядка, равного мощности бинарного отношения (рис. 7).
 М = {1, 2, 3, 4}, R = {(1, 2), (1, 4), (2, 3), (2, 4), (3, 4), (4, 1)} (рис. 7а).
М = {1, 2, 3, 4}, R = {(1, 2), (1, 4), (2, 3), (2, 4), (3, 4), (4, 1)} (рис. 7а).
Рис. 7. Графическое представление отношений
На рис. 7б и 7в представлены также графы тождественного отношения IМ и универсального отношения UМ.
Свойства отношений
Основнымисвойствами отношений являются:
– рефлексивность; – симметричность; – транзитивность; – антисимметричность;
Рефлексивность означает: справедливо xrx для любогоx Î M.
В графе отношения все вершиныимеют петли. (например, отношение «жить в одном городе» – рефлексивно);
R – антирефлексивно, если ни для какого a Î M имеет место a R a (например, отношение «быть сыном» – антирефлексивно);
Симметричность:xry Þ yrx. (например, отношение «учиться в одном институте» – симметрично)
При этом может быть и «пустая» симметричность когда нет xry («на нет и суда нет»). В графе соответствия каждая дуга имеет пару, но может быть и отсутствие связи между двумя вершинами.
Транзитивность:xry и yrz Þ xrz. «быть моложе» – транзитивно
Для каждой пары связанных непрямовершин существует и прямая связь (замыкающая образующийся многоугольник в графе отношения).
Транзитивность может быть и вырожденная (пустая, когда условие в левой части (до двойной стрелки) не выполняется). Здесь опять «на нет и суда нет».
Антисимметричность:xry и yrx Þ x = y. т.е. ни для каких различных элементов a, b (a ¹ b) не выполняется одновременно a R b и b R a (например, отношения «быть сыном», «быть начальником» – антисимметричны);
В графе отношений нет ни однойдвойной связи. И антисимметричность может быть пустой – вообще нет никакой прямой связи между двумя вершинами. Таким образом, в графе отношений допускаются только одинарные прямые связи.
асимметричность,… означает: прямые связи есть и двойные, и одинарные, и «никакие», т.е. нет ни симметричности, ни антисимметричности.
Свойства симметричности и антисимметричности не являются взаимно исключающими. Они могут “сосуществовать”. Правда, это возможно только в пустом варианте (рис. 8.)

Рис. 8. Примеры одновременных симметричности и антисимметричности
Отмеченные выше свойства отношений являются относительно редкими. Например, отношение, представленное графом на рис. 9, не является ни рефлексивным (P), ни симметричным (C), ни транзитивным (T) и ни антисимметричным (А).
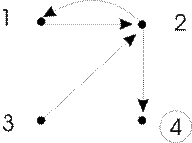 |
Рис. 9. Пример отношения.
Наконец, отметим ошибочность утверждения о том, что из симметричности и транзитивности якобы вытекает рефлексивность, т.е. что последнее свойство является производным от первых двух и петли в графе отношения появляются сами собой:
С: xry Þ yrx, А: xry и yrz Þ xrz;
при x = z получается как будто рефлексивность:
Р: xrx.
На самом деле это, конечно, не так. Убедиться в этом (доказать это) предоставляется читателю. (На примере?)

Пример: А={1,2,3}
r1={(1,1), (3,3), (1,2)} нерефлексивно, несимметрично, транзитивно
r2={(1,1), (3,3), (2,2)} рефлексивно, симметрично, транзитивно, эквивалентно на А, антисимметрично
r3={(1,2), (2,1)} антирефлексивно, симметрично, нетранзитивно
r4={(1,1), (3,3), (1,2), (2,1)} нерефлексивно, симметрично, нетранзитивно
r5={(1,1)} нерефлексивно, симметрично, транзитивно
r6={(1,2)} антирефлексивно, несимметрично, транзитивно
r7=r2È{(1,3), (3,1)} эквивалентно
r8=r2È{(1,3), (3,1), (2,3)} рефлексивно, несимметрично, нетранзитивно
Пусть задано некоторое множество А, разбиение будем называть U.
Определение: Совокупность подмножеств множества А будем называть разбиением данного множества, если:
1) АiÇAj=Æ, i¹j
2) 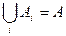 .
.
Пример: Дано множество В=R=(-¥;1)È[1;2] È[2;¥)
А1 А2 А3
Является ли разбиением данные подмножества?
U={А1,А2,А3} - не является
Пусть задано множество В={-1;4;7}
U1={-1,{4,7}} не является разбиением
U2={{-1,4,7}} является разбиением
U3={{-1},{4},{7}} является разбиением
U4={{-1,4},{7}} является разбиением
U5={{-1,4},{4,7}} не является разбиением
Отношение эквивалентности
Предварительно определим два таких понятия.
Покрытие множества– это совокупность его подмножеств, совместно накрывающих это непустое множество: 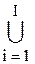 Мi = M, М ¹ Æ.
Мi = M, М ¹ Æ.
Например, {M1, M2} является покрытием множеств M1 È M2.
Разбиение множества – частный случай покрытия, когда составляющие подмножества попарно не пересекаются: 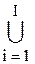 Мi = M,
Мi = M,
Mi1 Ç Mi2 ( i1 ¹ i2) = Æ.
Например, для универсального множества:
E = { М1 Ç М2, М1 Ç М2¢, М1¢ Ç М2, М1¢ Ç М2,¢}r.
Здесь индекс «r» («разбивание») обязателен, иначе получается неравенство мощностей слева и справа (справа – всего 4). В подмножествах разбиения каждый элемент M представлен только один раз.
Отношение эквивалентности– это первое замечательное теоретико-множественное отношение. Оно обладает тремя свойствами: рефлексивность, симметричность и транзитивность. По-другому говорят: любое РСТ-отношение – это отношение эквивалентности. Таковым является, например, обычное математическое равенство (« = »).
Отношение эквивалентности r разбивает множество М на классы эквивалентности: M / r. Между элементами каждого такого класса существует РСТ-отношение. Класс эквивалентности обозначается с использованием квадратных скобок. Внутри указывается любой элемент класса.
Например, широко используемые в теории чисел сравнения задают разбиение множества целых чисел Zна m классов эквивалентности, где m – некоторый модульсравнения: rm ={(x, y): x – y = k m, m Î N, k Î Z}.
При m=5 получаем: [1]={6, 11, 16, –4, 1, …},
[34]={29, 39, 4, …},
… …
Фактически различных классов эквивалентности здесь всего 5 – столько «простых» вычетовпо модулю 5. Эти вычеты (остатки от деления на 5): 0, 1, 2, 3, 4.
[0] = {… , –5, 0, 5, 10, …},
[1] = {… , –4, 1, 6, 11, …},
… …
[4] = {… , –1, 4, 9, 14, …}.
Кстати, сами сравнения записываются в виде:
0 º 5 (mod 5),
1 º –4 (mod 5),
… …
Они обладают многими свойствами, аналогичными свойствам обычных равенств. Но это уже специальная тема.


Отношение порядка
Это второе «замечательное» отношение (в математическом анализе есть второй замечательный предел, определяющий константу e = 2,71828…:  ).
).
Частичный порядок на множестве M – это любое рефлексивное, транзитивное и антисимметричное (РТА-) отношение. В обычной математике ему соответствует отношение нестрогого неравенства « £ ».
Наиболее важное свойство отношения порядка – его транзитивность.
Кстати, отношение £ и < (строгое неравенство) связаны очень просто:
а < b Û а £ b и а ¹ b, а £ b Û а < b или а = b.
Видно, что отношение строгого порядка нерефлексивно.
Полное отношение порядка r на M означает, что для любых элементов x, y Î M выполняется xry и/или yrx, причем r – это РТА- отношение.
В связи c упорядочиванием элементов вводится множество таких понятий:
–верхняя граница элементовx, y (u Î M, x £ u, y £ u);
– нижняя граница элементов x, y (v Î M, v £ x, v £ y);
–верхняя грань элементов x, y («супремум»); m Î M, m £ "u; здесь верхних границ u – множество; m = sup (x, y));
– нижняя грань элементов x, y («инфимум»; n Î M, "v £ n; n = inf (x, y));
– замкнутый интервал значений ([a, b] = {x : x Î R, a £ x £ b } );
–открытый интервал ( ] a, b [ = { x : x Î R, a < x < b} );
–полуоткрытый интервал ( ] a, b ] = { x : x Î R, a < x £ b} или [ a, b [ = {x : x Î R,
a £ x < b} );
–концевые точки интервала (a, b).


Глава 1. Логика высказываний
Основные понятия

Истинностные значения «истина» и «ложь» будем обозначать прописными буквами И и Л соответственно.
Высказывание называется простым (элементарным), если оно рассматривается как некое неделимое целое. Сложным (составным) называется высказывание, составленное из простых с помощью логических связок (операций).
Основными логическими операциями над высказываниями являются: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность, неравнозначность.
Отрицанием (инверсией) высказывания P называется высказывание, истинное тогда и только тогда, когда высказывание P ложно, и ложное в противном случае. Обозначения: 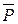 , ù P. Читается: «не P». Отрицание определяется таблицей истинности (табл. 4.1).
, ù P. Читается: «не P». Отрицание определяется таблицей истинности (табл. 4.1).
Конъюнкцией (операцией «И», логическим произведением) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания, и ложное во всех других случаях. Обозначения: P&Q, P×Q, PÙQ. Читается: «P и Q». Конъюнкция определяется таблицей истинности (табл. 4.2).
Дизъюнкцией (операцией «ИЛИ», логической суммой) двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны, и истинное – во всех других случаях. Обозначения: PÚQ, P+Q. Читается: «P или Q» (понимается как неразделительное «или»). Дизъюнкция определяется таблицей истинности (табл. 4.3).
Импликацией (логическим следованием) двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда P истинно, а Q ложно, и истинное – во всех других случаях. Обозначения: P®Q, PÉQ. Читается: «если P, то Q», «P влечет Q»). Высказывание P называется посылкой импликации, а высказывание Q - заключением. Импликация определяется таблицей истинности (табл. 4.4).
Эквивалентностью (равнозначностью, эквиваленцией) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинностные значения P и Q совпадают, и ложное в противном случае. Обозначения: P«Q, P~Q, PºQ. Читается: «P эквивалентно Q», «P, если и только если Q», «P равнозначно Q». Эквивалентность определяется таблицей истинности (табл. 4.5).
Неравнозначностью (исключающим «ИЛИ», сложением по модулю 2) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинностные значения P и Q не совпадают, и ложное – в противном случае. Обозначения: PÅQ, PDQ. Читается: «P неравнозначно Q», «либо P, либо Q», «или P, или Q» (понимается – в разделительном смысле). Неравнозначность определяется таблицей истинности (табл. 4.6).
Буквы, обозначающие высказывания, логические связки и скобки, составляют алфавит языков логики высказываний: алгебры логики и исчисления высказываний<
