Проектирование систем типа Мамдани.

Рассмотрим основные этапы проектирования систем типа Мамдани на примере создания системы нечеткого логического вывода, моделирующей зависимость 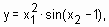, 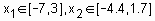. Проектирование системы нечеткого логического вывода будем проводить на основе графического изображения указанной зависимости.

Для построения трехмерного изображения функции 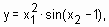в области 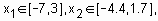составим следующую программу:

%Построение графика функции y=x1^2*sin(x2-1)

%в области x1є[-7,3] и x2є[-4.4,1.7].

n=15;

x1=-7:10/(n-1):3;

x2=-4.4:6.1/(n-1):1.7;

y=zeros(n,n);

for j=1:n

y(j,:)=x1.^2*sin(x2(j)-1);

end

surf(x1,x2,y)

xlabel('x1')

ylabel('x2')

zlabel('y')

title('Target');

В результате выполнения программы получим графическое изображение, приведенное на рисунке 4.13. Проектирование системы нечеткого логического вывода, соответствующей приведенному графику, состоит в выполнении следующей последовательности шагов.

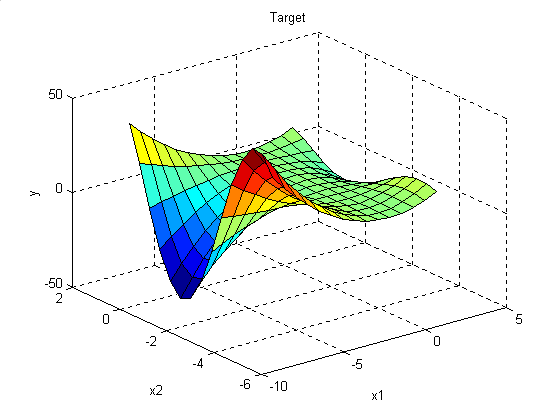
Рисунок 4.13 - Эталонная поверхность

Шаг 1. Для загрузки основного fis-редактора напечатаем слова fuzzy в командной строке.

Шаг 2. Добавим вторую входную переменную. Для этого в меню Edit выбираем команду Add input.

Шаг 3. Переименуем первую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input1, введем новое обозначение x1 в поле редактирования имени текущей переменной и нажмем <Enter>.

Шаг 4. Переименуем вторую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input2, введем новое обозначение x2 в поле редактирования имени текущей переменной и нажмем <Enter>.

Шаг 5. Переименуем выходную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке output1, введем новое обозначение y в поле редактирования имени текущей переменной и нажмем <Enter>.

Шаг 6. Зададим имя системы. Для этого в меню File выбираем в подменю Export команду To disk и вводим имя файла, например, first.

Шаг 7. Перейдем в редактор функций принадлежности. Для этого сделаем двойной щелчок левой кнопкой мыши на блоке x1.

Шаг 8. Зададим диапазон изменения переменной x1. Для этого напечатаем -7 3 в поле Range (рисунок 4.14) и нажмем <Enter>.

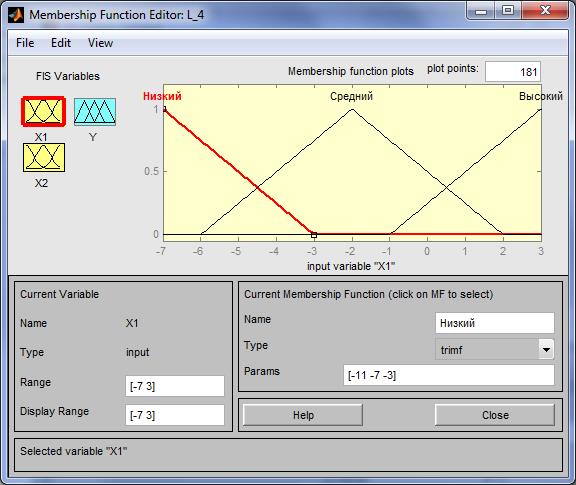
Рисунок 4.14 - Функции принадлежности переменной x1

Шаг 9. Зададим функции принадлежности переменной x1. Для лингвистической оценки этой переменной будем использовать 3 терма с треугольными функциями принадлежности. Для этого в меню Edit выберем команду Add MFs... В результате появиться диалоговое окно выбора типа и количества функций принадлежностей. По умолчанию это 3 терма с треугольными функциями принадлежности. Поэтому просто нажимаем <Enter>.

Шаг 10. Зададим наименования термов переменной x1. Для этого делаем один щелчок левой кнопкой мыши по графику первой функции принадлежности (рисунок 4.14). Затем вводим наименование терма, например, Низкий, в поле Name и нажмем <Enter>. Затем делаем один щелчок левой кнопкой мыши по графику второй функции принадлежности и вводим наименование терма, например, Средний, в поле Name и нажмем <Enter>. Еще раз делаем один щелчок левой кнопкой мыши по графику третьей функции принадлежности и вводим наименование терма, например, Высокий, в поле Name и нажмем <Enter>. В результате получим графическое окно, изображенное на рисунке 4.14.

Шаг 11. Зададим функции принадлежности переменной x2. Для лингвистической оценки этой переменной будем использовать 5 термов с гауссовскими функциями принадлежности. Для этого активизируем переменную x2 с помощью щелчка левой кнопки мыши на блоке x2. Зададим диапазон изменения переменной x2. Для этого напечатаем -4.4 1.7 в поле Range (рисунок 4.15) и нажмем<Enter>. Затем в меню Edit выберем команду Add MFs.... В появившимся диалоговом окне выбираем тип функции принадлежности gaussmfв поле MF type и 5 термов в поле Number of MFs. После этого нажимаем <Enter>.

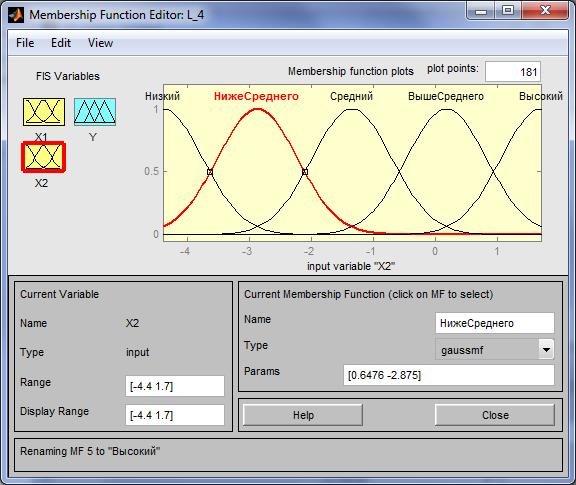
Рисунок 4.15 - Функции принадлежности переменной x2

Шаг 12. По аналогии с шагом 10 зададим следующие наименования термов переменной x2: Низкий, Ниже среднего, Средний, Выше среднего, Высокий. В результате получим графическое окно, изображенное на рисунке 4.15.

Шаг 13. Зададим функции принадлежности переменной y. Для лингвистической оценки этой переменной будем использовать 5 термов с треугольными функциями принадлежности. Для этого активизируем переменную y с помощью щелчка левой кнопки мыши на блоке y. Зададим диапазон изменения переменной y. Для этого напечатаем -50 50 в поле Range (рисунок 4.16) и нажмем<Enter>.Затем в меню Edit выберем команду Add MFs.... В появившимся диалоговом окне выбираем 5 термов в поле Number of MFs. После этого нажимаем <Enter>.

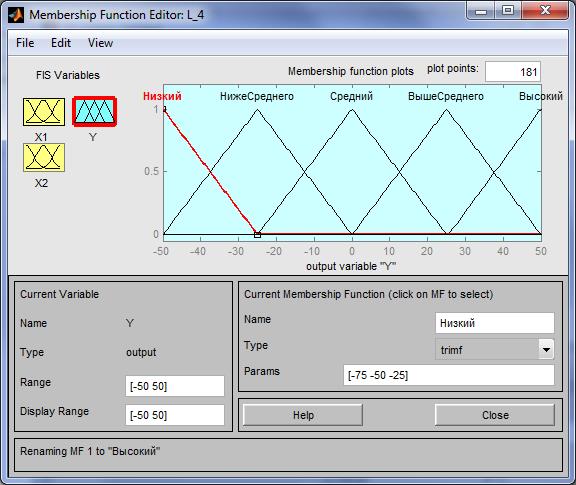
Рисунок 4.16 - Функции принадлежности переменной y

Шаг 14. По аналогии с шагом 10 зададим следующие наименования термов переменной y: Низкий, Ниже среднего, Средний, Выше среднего, Высокий. В результате получим графическое окно, изображенное на рисунке 4.16.

Шаг 15. Перейдем в редактор базы знаний RuleEditor. Для этого выберем в меню Edit команду Edit rules....

Шаг 16. На основе визуального наблюдения за графиком, изображенным на рисунке 4.13 сформулируем следующие девять правил:

Если x1=Средний, то y=Средний;

Если x1=Низкий и x2=Низкий, то y=Высокий;

Если x1=Низкий и x2=Высокий, то y=Высокий;

Если x1=Высокий и x2=Высокий, то y=Выше Среднего;

Если x1=Высокий и x2=Низкий, то y=Выше Среднего;

Если x1=Высокий и x2=Средний, то y=Средний;

Если x1=Низкий и x2=Средний, то y=Низкий;

Если x1=Высокий и x2=Выше Среднего, то y=Средний;

Если x1=Высокий и x2=Ниже Среднего, то y=Средний.

Для ввода правила необходимо выбрать в меню соответствующую комбинацию термов и нажать кнопку Add rule. На рисунке 4.17 изображено окно редактора базы знаний после ввода всех девяти правил. Число, приведенное в скобках в конце каждого правила представляет собой весовым коэффициент соответствующего правила.

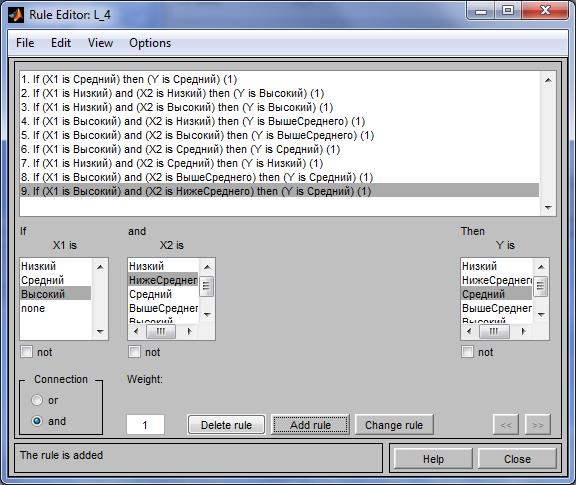
Рисунок 4.17 - База знаний в RuleEditor

Шаг 17. Сохраним созданную систему. Для этого в меню File выбираем в подменю Exportкоманду To disk.

На рисунке 4.18 приведено окно визуализации нечеткого логического вывода. Это окно активизируется командой View rules... меню View. В поле Input указываются значения входных переменных, для которых выполняется логический вывод.

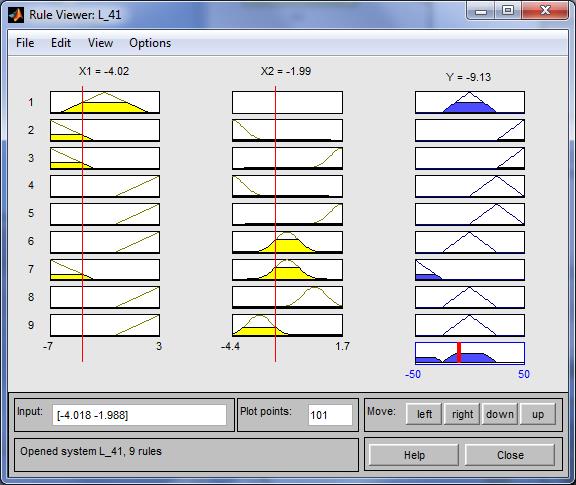
Рисунок 4.18 - Визуализация нечеткого логического вывода в RuleViewer

На рисунке 4.19 приведена поверхность «входы-выход», соответствующая синтезированной нечеткой системе. Для вывода этого окна необходимо использовать команду View surface... меню View. Сравнивая поверхности на рисунке 4.13 и на рисунке 4.19 можно сделать вывод, что нечеткие правила достаточно хорошо описывают сложную нелинейную зависимость.

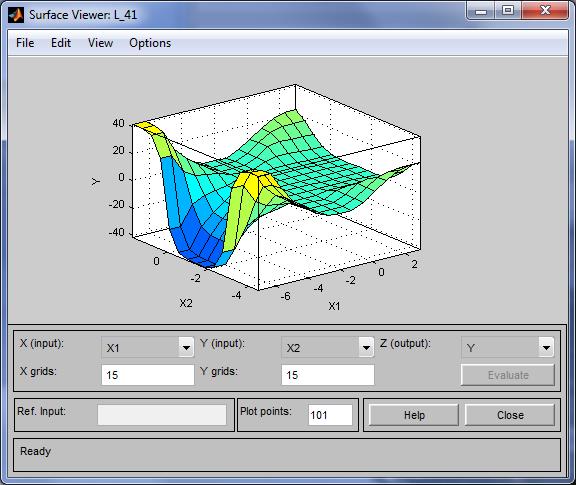
Рисунок 4.19 - Поверхность «входы-выход» в окне SurfaceViwer

Контрольные вопросы к защите

1. Для чего предназначен FIS-редактор?

2. Назовите основные элементы окна FIS-редактора?

3. Опишите редактор функций принадлежности?

4. Какого типа имеются функции принадлежности в пакете fuzzy logic?

5. Опишите окно редактора баз знаний?

6. Каким образом можно произвести визуализацию нечеткого логического вывода?

7. Что такое визуализация поверхности типа «входы-выходы»?