Простые числа специального типа
Числа Мерсенна — числа вида  , где
, где 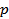 — простое число.
— простое число.
Числа Вудалла — числа вида  , где
, где 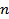 — натуральное число.
— натуральное число.
Числа Прота — числа вида  , где
, где 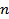 — натуральное число, а
— натуральное число, а  нечетно и
нечетно и  .
.
Числа Кулдена — числа вида  , где
, где 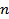 — натуральное число. При
— натуральное число. При 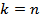 числа Кулдена являются частным случаем чисел Прота.
числа Кулдена являются частным случаем чисел Прота.
Числа Ферма — числа вида 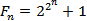 , где
, где 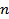 — целое положительное число. Числа Ферма являются частным случаем чисел Прота при
— целое положительное число. Числа Ферма являются частным случаем чисел Прота при 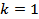 и
и 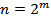 . По состоянию на ноябрь 2011 года известно только 5 простых чисел Ферма для
. По состоянию на ноябрь 2011 года известно только 5 простых чисел Ферма для  и высказана гипотеза, что других простых чисел Ферма нет.
и высказана гипотеза, что других простых чисел Ферма нет.
Принято отмечать наибольшие простые числа. Один из рекордов поставил в свое время Эйлер (1707-1783), найдя простое число  . По состоянию на ноябрь 2011 года наибольшим простым числом является
. По состоянию на ноябрь 2011 года наибольшим простым числом является 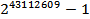 . Оно относится к числам Мерсенна и содержит 12 978 189 десятичных цифр.
. Оно относится к числам Мерсенна и содержит 12 978 189 десятичных цифр.
