Вращение вокруг осей, расположенных параллельно плоскости проекций

Задача: плоскость общего положения преобразовать в плоскость уровня.

На рис. 2.4 задана плоскость ABC общего положения. Рассмотрим вращение вокруг горизонтали, для чего через проекцию B'' зададим проекцию горизонтали h''. Через В' и 1'проведем горизонтальную проекцию горизонтали h'. При вращении плоскости ABC вокруг горизонтали, горизонтальные проекции точек A' и C'будут перемещаться в горизонтально проецирующих плоскостях перпендикулярных к h'.

Остановить вращение надо в тот момент, когда плоскость ABC на горизонтальной плоскости проекций отобразится в натуральную величину. Для этого надо найти натуральную величину радиуса вращения, например, точки A (Н. В. расстояния от A' до h' ). Это можно сделать, воспользовавшись способом прямоугольного треугольника [2, стр. 24]. Или см. рис. 5.7, а также рис. 5.8. Отложим найденную величину (отрезок от А⁰ до до центра вращения точки A') на горизонтально проецирующей плоскости, в которой вращается точка А, получим ее новое положение A'₁. Это и будет новое положение проекции точки A', когда плоскость ABC преобразуется в плоскость уровня.

Точка 1 (1') лежит на оси вращения, поэтому своего положения при вращении плоскости АВС не изменит. Проекция точки C' перемещается в своей горизонтально проецирующей плоскости, перпендикулярной кh', поэтому, проведя прямую из проекции A'₁ через 1' до пересечения с горизонтально проецирующей плоскостью точки C', получим новое положение точки C'₁. Соединив точки A'₁, B', C'₁ получим новое положение треугольника ABC, преобразованного в плоскость уровня. О способах преобразования проекционного чертежа см. [2, стр. 49]

Теперь вы должны выполнить задачи 9 и 10 контрольной работы

Практическое занятие 4.
Способы преобразования прямоугольных проекций

Способы преобразования прямоугольных проекций применяются при решении многих практических задач.

При решении задач № 9, №11 и, возможно, при решении задач №12 и №13 необходимо применить способ замены плоскостей (см. рис. 2.1 – а - прямую общего положения преобразовать в прямую уровня; рис. 2.1-б - прямую общего положения преобразовать в проецирующую прямую; рис. 2.2 - плоскость общего положения преобразовать в проецирующую и далее - в плоскость уровня.), или способ вращения (см. рис.2.3 - вращение вокруг осей, расположенных перпендикулярно плоскости проекций; рис.2.4 - вращение вокруг осей, расположенных параллельно плоскости проекций).

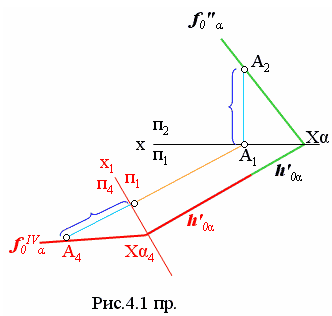
На рис. 4.1 пр. показано преобразование плоскости общего положения, заданной следами, в проецирующую. Для придания наглядности в системе х (п₁/п₂) следы плоскости α выделены зеленым цветом. Новая система х₁ (п₁/п₄) выделена красным цветом. Горизонтальный след плоскости h'_{0 α} условно выделен двумя цветами (зеленым для исходной системы и он же красным для преобразованной).

Алгоритм преобразования следующий. Задаем точку, принадлежащую плоскости α – А (А₂ А₁) . Задаем новую ось х₁ перпендикулярно горизонтальному следу h'_{0 α}. Образовалась новая система х₁(п₁/п₄). На оси х₁ отмечаем точку схода следов Хα₄. По линиям связи переносим точку А (А₄) в плоскость п₄ . Через новую точку схода следов и проекцию А₄ задаем след f₀^IV, являющийся следом проецирующей плоскости.

По данной теме Вам необходимо выполнить в контрольной работе задачу №9.

Тема 3

Поверхности

Мир поверхностей разнообразен и безграничен. Он простирается от простейшей поверхности – плоскости, до сложнейших, причудливых форм криволинейных поверхностей, не поддающихся точному математическому описанию. Под поверхностью мы будем понимать границу материального тела, не имеющую третьего измерения – толщины. Поверхность можно задать следующими способами: аналитическим; кинематическим; каркасным.

Аналитический способ задания поверхностей рассматривается в соответствующих разделах курса высшей математики. Под кинематическим способом задания поверхностей подразумевается «след» непрерывно перемещающейся линии в пространстве по определенному закону. Закон движения перемещающейся линии – образующей, может определять другая линия (или линии) – направляющая. При этом подразумевается, что образующая скользит по направляющей.

Каркасный способ задания поверхности упрощенно можно представить как набор линий – продольных и поперечных.

Кинематический способ задания поверхности подводит к понятию определителя поверхности, который состоит из двух частей: геометрической и алгоритмической. Геометрическая часть определяет вид и способ задания образующей и направляющей. Алгоритмическая часть определяет закон движения образующей.

Многогранники

В определении понятия многогранники существует несколько суждений. Рассматривая заданиеповерхности многогранника с позиций кинематического способа, можно сказать следующее. Движение прямолинейной образующей по ломаной направляющей образует гранную поверхность. Если образующая движется по направляющей «параллельно самой себе», поверхность называется призматической. Если одна точка образующей закреплена неподвижно – поверхность называется пирамидальной. [2, стр. 62]

В некоторых учебниках вместо поверхности многогранников рассматривается геометрическое тело, ограниченное со всех сторон плоскими многоугольниками [8, стр. 105]. Плоские многоугольники, ограничивающие многогранник, являются его гранями, а линии пересечения граней – его ребрами.