Пропедевтика темы «Деление с остатком»
1. Практическая работа.
Учитель предлагает учащимся с помощью фигурок наборного полотна выполнить деление, записать и решить выражения.
Н а п р и м е р: учитель выставляет на наборное полотно 12 яблок.
– Как можно 12 яблок разделить между 3 детьми поровну? (Один из учащихся выполняет работу у доски.)
– Как записать то, что вы сейчас выполнили?
– Запись с комментированием:
12: 3 = 4
– Как можно 12 яблок разделить между 4 детьми поровну?
– Запишите то, что выполняли.
Запись с комментированием.
12 : 4 = 3
– Как можно 12 яблок разделить между 2 (6) детьми поровну?
– Запишите это.
Запись с комментированием:
12 : 2 = 6
12 : 6 = 2
Аналогичная работа проводится по рисункам с. 51 учебника (часть 2, задание 1).
2. Работа с учебником.
К задаче 2 (с. 51 учебника, часть 2) учащиеся выполняют рисунок и записывают решение задачи действием деления. (Один учащийся выполняет работу на доске с использованием фигурок наборного полотна.)
Работа над задачей 3 (с. 51 учебника, часть 2) является пропедевтической работой к изучению темы «Деление с остатком».
Работу можно построить следующим образом: после того как учащиеся прочитали задачу, учитель беседует с ними.
– Сколько дощечек идет на один скворечник? (Семь.)
– Сколько дощечек имеется? (Пятнадцать.)
– Можно из пятнадцати дощечек сделать один скворечник?
– Докажите это. (Если из пятнадцати дощечек взять семь на изготовление скворечника, то восемь дощечек останется.)
– Можно ли из пятнадцати дощечек сделать два скворечника?
– Как это узнать? (На один скворечник идёт 7 дощечек. Чтобы узнать, сколько дощечек идёт на 2 скворечника, надо 7 умножить на 2 или к 7 прибавить 7, получится 14. Из 15 дощечек возьмём 14 на изготовление скворечника, и 1 дощечка останется.)
– Можно ли из пятнадцати дощечек сделать три скворечника?
– Как это узнать? (На один скворечник идет 7 дощечек, а на 2 – 14. Чтобы узнать, сколько дощечек идет на 3 скворечника, надо к 14 прибавить ещё 7, получится 21. 21 больше 15, значит, 3 скворечника сделать нельзя.)
– Сколько же можно сделать скворечников из 15 дощечек? (Один, два.)
При работе над задачей 4 (с. 51 учебника, часть 2) учитель показывает учащимся краткую запись задачи, которая решается умножением.
– Прочитайте задачу.
– Выделите условие (вопрос).
– Какие слова используем в краткой записи?
– Что известно про Ваню?
– Что известно про Нину?
З а п и с ь:
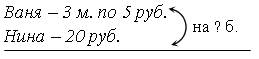
Решение задачи выполняется по действиям с объяснением.
– Можем сразу ответить на вопрос задачи?
– Почему?
– Как узнать: сколько денег у Вани?
– Запишите. (3 · 5 = 15 (руб.) у Вани.)
– Можем теперь ответить на вопрос задачи?
– Какое действие следует для этого выполнить?
– Запишите. (20 – 15 = 5 (руб.).)
– Сформулируйте ответ и запишите его.
V. Решение и сравнение выражений.
С комментированием выполняется задание 6 (с. 51 учебника, часть 2). Особое внимание следует уделить выражениям первого столбика.
Затем устно, с объяснением выполняется задание 5 (с. 51 учебника, часть 2), в котором учащиеся сравнивают выражения.
Далее учитель предлагает учащимся внимательно рассмотреть выражения, записанные на доске (учитель использует выражения из задания 9 (с. 51 учебника, часть 2).
– Что заметили?
– На какие группы можно разделить данные выражения? (Высказывания детей.)
– Найдите значения выражений. (Работа выполняется устно, с объяснением.)
– Разделите выражения на группы по их значениям.
VI. Домашнее задание.
Выполнить задание 7 (с. 51 учебника, часть 2).
VII. Итог урока.
– Что узнали сегодня на уроке?
– Всё ли было понятно?
– Оцените свою работу.
У р о к 109. РЕШЕНИЕ ЗАДАЧ ДЕЙСТВИЕМ ДЕЛЕНИЯ
Цели:формировать умение учащихся решать задачи действием деления; развивать вычислительные навыки; закреплять умение учеников решать уравнения и задачи изученных видов; развивать логическое мышление, внимание, наблюдательность.
Ход урока
I. Организационный момент.
II. Каллиграфическая минутка.
9 9 9 9 9 9
0 0 0 0 0 0
III. Устный счет.
1. Какое число и какой знак пропущены?
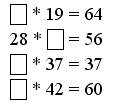
2. Задание 5 (с. 52 учебника, часть 2).
Учащиеся заполняют таблицу, которая записана на доске. Выполняя задание, дети повторяют термины «слагаемое», «сумма».
3. Сравните значения выражений:
2 · 5 * 2 · 4 3 · 6 * 3 · 3
2 · 7 * 7 · 2 8 · 3 * 3 · 8
2 · 8 * 9 · 2 3 · 4 * 7 · 3
– Можно ли сравнить значения этих выражений, не вычисляя их?
– Обоснуйте ваше мнение.
