Изображение на чертеже Сферы. Линии каркаса, очерк, точки и линии на поверхности сферы

Каркас поверхности. Если построить некоторое количество образующих по некоторому алгоритму, то получим каркас или сеть поверхности

Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.

Шаром называется тело, ограниченное сферической поверхностью.

Очерк поверхности.Линия пересечения проецирующей поверхности, огибающей заданную поверхность, с плоскостью проекций называется очерком поверхности.

Очерком поверхности называют проекции контурной линии.

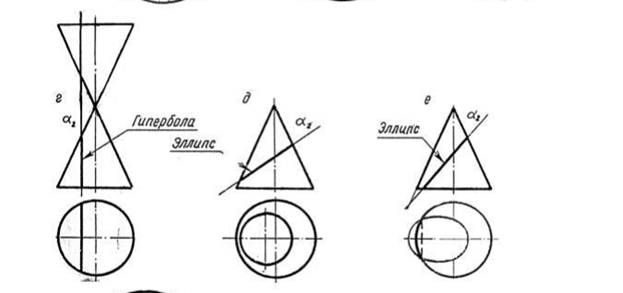
Сфера - на ортогональном чертеже сферическая поверхность задается

проекциями центра О (О1,О2,О3) и числовым значением радиуса r.

Наибольшая параллель называется экватором m (m1,m2,m3). Экватор - это

наибольшая окружность, параллельная горизонтальной плоскости проекций.

Фронтальный главный меридиан n (n1,n2,n3) - это наибольшая окружность,

параллельная фронтальной плоскости проекций. Профильный главный

меридиан р (р1,р2,р3) - это наибольшая окружность, параллельная

профильной плоскости проекций.

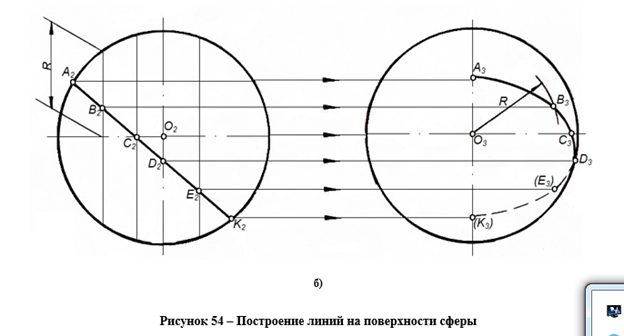
Точкапринадлежит поверхности сферы, если она принадлежит окружности этой сферы. На эпюре окружности для определения точек проводятся параллельно экватору или главным меридианам, так как в этом случае они параллельны плоскостям проекций и проецируются на них в натуральную величину.

Общие приемы построения линии пересечения поверхности плоскостью. Конические сечения.

КОНИЧЕСКИЕ СЕЧЕНИЯ,плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей через его вершину. С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек, удовлетворяющих уравнению второго порядка. За исключением вырожденных случаев, рассматриваемых в последнем разделе, коническими сечениями являются эллипсы, гиперболы или параболы.

При пересечении многогранной поверхности плоскостью в сечении получается плоский многоугольник, вершины которого есть точки пересечения ребер многогранника с секущей плоскостью, стороны – линии пересечения граней поверхности с секущей плоскостью. Стороны многоугольника видимы, если они лежат на видимых гранях, и невидимы, если – на невидимых. Если при построении сечения многогранника плоскостью секущая плоскость или грани являются проецирующими, то следует использовать вырождение их соответствующих проекций в прямые. При профильном расположении одного из ребер пирамиды необходимо, в первую очередь, строить профильную проекцию точки пересечения его с плоскостью, а затем уже горизонтальную. Кривые поверхности с плоскостью в общем случае пересекаются по плоским кривым линиям.

Линией пересечения боковой поверхности прямого кругового конуса с плоскостью могут быть две прямые – образующие конуса (рис. 9, а), если плоскость проходит через вершину конуса; окружность (рис. 9, б), если плоскость перпендикулярна к оси конуса; парабола (рис. 9, в), если плоскость параллельна одной образующей конуса; гипербола (рис. 9, г), если плоскость параллельна двум образующим конуса; эллипс (рис. 9, д, е), если плоскость пересекает все образующие конуса и не перпендикулярна к его оси.