Иначе говора, требуется решить задачу Коши

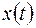Предположим, что правая часть уравнения (5.1) и искомая функция вместе со своими производными до 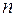-го порядка включительно являются оригиналами. Так как функция 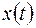является решением уравнения (5.1), удовлетворяющим (5.2), то после подстановки этой функции в (5.1) мы получим тождество. Значит, функция, стоящая в левой части (5.1), и функция имеют одно и то же изображение Лапласа. Поэтому имеет место равенство

.

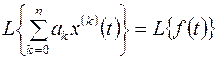В силу свойства линейности изображения запишем

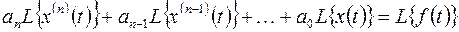. (5.3)

Пусть

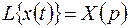и 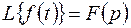. (5.4)

По теореме о дифференцировании оригинала с учетом начальных условий (5.2) будем иметь

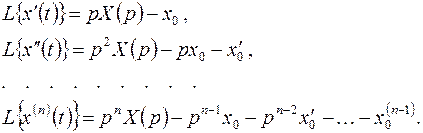(5.5)

Подставляя в равенство (5.3) вместо изображений функций , 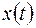и ее производных выражения (5.4) и (5.5), получим

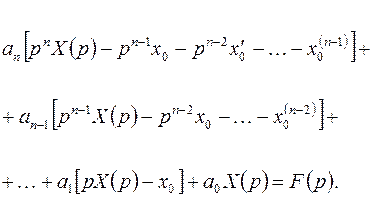(5.6)

Уравнение (5.6) а также (5.3) называют уравнением в изображениях или операторным уравнением. Операторное уравнение для данного дифференциального уравнения (5.1) является алгебраическим уравнением первой степени относительно изображения 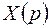искомой функции .

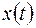Перепишем уравнение (5.6) так:

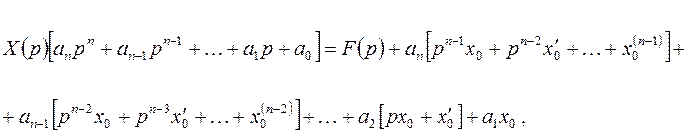
Откуда найдем изображение

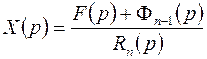, (5.7)

где 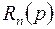и 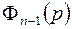– многочлены от 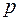соответственно степене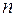й и .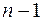

.

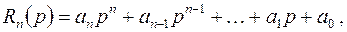
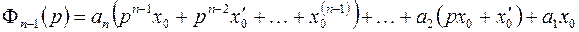Если, в частности, начальные условия нулевые, то формула (5.7) упростится:

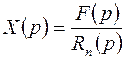. (5.7 а)

Теперь по найденному изображению 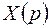отыскиваем оригинал 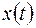(или непосредственно по таблице или по теореме обращения). В силу теоремы единственности оригинал 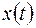будет искомым решением задачи Коши.

Пример 5.1. Найти решение уравнения

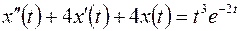
при начальных условиях: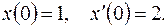

Решение. Переходим к уравнению в изображениях, полагая, что 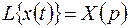. Найдем изображения для 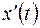и :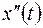

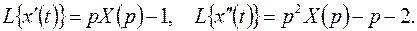
Из соответствия 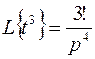(см. в таблице оригиналов и изображений формулу (3)), пользуясь теоремой затухания, найдем изображение правой части уравнения

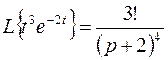
Тогда операторное уравнение запишется в виде

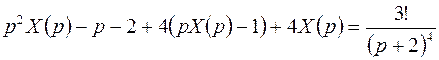
Или

,

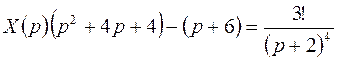Откуда

.

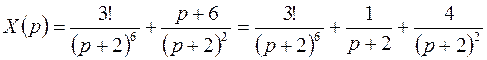С помощью таблицы соответствий восстанавливаем оригиналы для каждого слагаемого:

;

.

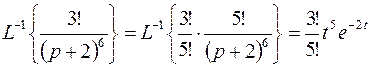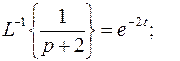
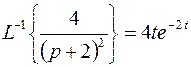Следовательно, .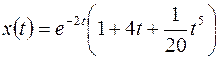

Обсудим подробнее преимущества операционного метода интегрирования дифференциальных уравнений. При решении задачи Коши для линейного неоднородного дифференциального уравнения 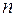-го порядка обычным путем, рассмотренным в теории обыкновенных дифференциальных уравнений, необходимо сначала найти общее решение, которое зависит от 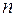произвольных постоянных 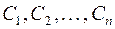. Определение произвольных постоянных требует дополнительного решения системы 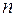линейных алгебраических уравнений, определяющих при 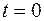искомую функцию и ее производные до

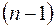-го порядка включительно, а это для случая 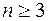довольно громоздко и утомительно. Применение преобразования Лапласа сильно упрощает решение задачи потому, что, во-первых, надо решать не дифференциальное уравнение относительно оригинала, а алгебраическое уравнение относительно его изображения, во-вторых, не требуется находить значения произвольных постоянных, исходя из начальных условий, так как они автоматически вводятся в решение относительно изображения, а затем и в решение относительно оригинала. Наиболее частый на практике случай нулевых начальных условий при классическом методе решения не освобождает от решения упомянутой системы алгебраических уравнений относительно произвольных постоянных. Использование в этом случае операционного метода обеспечивает исключительно простой ход вычислений. Кроме того, отыскание общего решения неоднородных линейных дифференциальных уравнений традиционным способом состоит из двух этапов: решения соответствующего однородного уравнения и затем решения неоднородного уравнения по методу вариации постоянных. Операционный метод позволяет сразу решать неоднородное уравнение. Если же требуется найти общее, а не частное решение дифференциального уравнения, то и это можно сделать операционным методом.

И в том случае, когда в правой части уравнения типа (5.1) стоит кусочно-непрерывная функция , которую записывают с помощью нескольких аналитических выражений, успешно применяется операционный метод. Это является еще одним преимуществом операционного метода по сравнению с традиционными: при использовании последних уравнений, правая часть которого имеет различный вид на разных интервалах изменения аргумента, пришлось бы интегрировать по этапам, т.е. на каждом таком интервале по отдельности. При этом на каждом этапе пришлось бы искать свое решение неоднородного уравнения, отвечающее данному виду правой части, определять свои начальные условия и по найденным начальным условиям определять свои значения произвольных постоянных, входящих в решение. По теореме запаздывания находят изображение кусочно-непрерывной функции, после чего получают одно операторное уравнение относительно изображения искомого решения задачи Коши.

Пример 5.2. Найти решение уравнения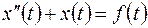

при нулевых начальных условиях; 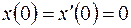, если функции задана графиком, изображенным на рис.5.1.

Решение. Исходя из графика функции , получим ее аналитическое представление