Кинетостатический расчет механизма
Кинетостатическим, в отличие от статического, называется расчет механизма с учетом сил инерции. Целью кинетостатического расчета является определение сил, действующих на звенья механизма, реакций в кинематических парах и затрат энергии, необходимой для приведения механизма в движение и выполнения им работы в соответствии с его назначением.
Для выполнения кинетостатического расчета необходимо иметь:
- кинематическую схему (план) механизма;
- планы скоростей и ускорений для заданного положения звеньев механизма;
-величину масс подвижных звеньев и моменты их инерции (для звеньев, совершающих вращательное и плоскопараллельное движения);
-закон изменения силы полезного сопротивления при работе механизма.
Кинетостатический расчет начинается с выделения из механизма структурных групп Ассура, являющихся статически определимыми системами (рис.7). В сложных механизмах расчет начинается с группы, к которой приложена сила полезного сопротивления (Рс). В рассматриваемом механизме расчет можно начинать с любой из них. Предварительно структурную группу необходимо изобразить на чертеже в таком положении, в котором она находится в механизме с соблюдением масштаба. Допускается увеличить размеры звеньев с изменением масштаба изображения. Для выделенной группы определяем действующие на ее звенья силы.
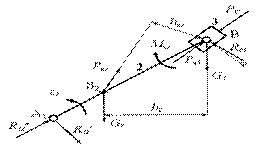
Рис.7 Расчетная схема для 1-ой группы Ассура
На звенья в их центрах масс действуют силы тяжести G2 и G3.
В тех же точках приложены силы инерции этих звеньев Р2 и Р3, которые направлены против ускорений этих звеньев.
На рабочую поверхность поршня, в зависимости от фазы, в которой находится поршневая группа, может действовать сила полезного сопротивления (Рс) - сила давления сжатого воздуха в цилиндре.
R63 – реакция стенок цилиндра (звено 6) на поршень 3. R63 является геометрической суммой силы нормального давления N и силы трения F, направленной против движения поршня. Реакция отклонена от силы N на величину угла трения φ, тангенс которого равен коэффициенту трения 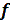 . При расчетах механизмов принимают
. При расчетах механизмов принимают 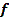 =0,1 (полусухое трение), следовательно
=0,1 (полусухое трение), следовательно 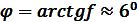

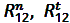 - соответственно нормальная и тангенциальная составляющие реакции со стороны отброшенного звена 1. Нормальная составляющая направляется произвольно по шатуну.
- соответственно нормальная и тангенциальная составляющие реакции со стороны отброшенного звена 1. Нормальная составляющая направляется произвольно по шатуну.
Реакция в точке В, где осуществляется соединение шатуна с поршнем является внутренней силой и не влияет на равновесие сил, действующих на эту группу. На плане сил определяется, как сумма всех сил, действующих на какое-либо звено рассматриваемой группы.
Так как группа Ассура является статически определимой системой составляем векторное уравнение равновесия сил для определения неизвестных величин:
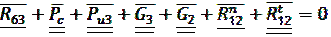 , (17)
, (17)
Для графического решения векторного уравнении (17) необходимо добиться, чтобы в нем осталось две неизвестные величины.
Сила тяжести шатуна:
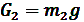 [Н]
[Н]
Сила тяжести поршня:
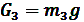 [Н]
[Н]
Сила инерции шатуна :
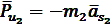 [Н]
[Н]
Сила инерции поршня:
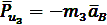 [Н]
[Н]
Силы инерции приложены в центрах масс соответствующих звеньев и направлены против векторов ускорений этих звеньев (рис.7).
К звену 2 необходимо приложить еще момент сил инерции, который направлен противоположно угловому ускорению ε2:
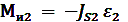 [Н м],
[Н м],
где JS2 - момент инерции звена относительно центра масс.
Из уравнения равновесия моментов всех сил относительно т.В (ΣМВ=0) определяем тангенциальную составляющую R12t. Знак момента сил выбирается произвольно. Примем в нашем случае положительное направление моментов против часовой стрелки:
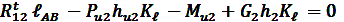 , (18)
, (18)
где h2, hи2 - плечи действия соответствующих сил относительно т.В - измеряются на чертеже и подставляются в мм.
Из уравнения (18) находим:
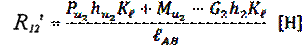
Силу полезного сопротивления Рс определяем по формуле:
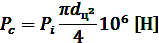 ,
,
где Pi - давление сжатого воздуха на единицу площади рабочей поверхности поршня (МПа) в зависимости от фазы работы поршневой группы;
πdц2/4 - площадь рабочей поверхности поршня (м2);
dц - диаметр рабочей поверхности поршня.
Давление Pi определяется с помощью индикаторной диаграммы, в соответствии с процессом, происходящим в цилиндре компрессора (всасывание, сжатие, нагнетание). Если поршень движется к оси вращения кривошипа, то данной поршневой группой реализуется фаза всасывания воздуха.
Индикаторная диаграмма характеризует изменение давления воздуха в цилиндре за цикл, соответствующий повороту кривошипа на 360°и строится по данным, представленным в таблице 1:
Таблица 1 Характерные точки для построения индикаторной диаграммы
| SB/ SBmax | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
| Pi/Pmax при всасывании | 1,0 | 0,3 | |||||||||
| Pi/Pmax при сжатии | 1,0 | 1,0 | 1,0 | 0,55 | 0,38 | 0,27 | 0,18 | 0,12 | 0,08 | 0,04 |
Здесь: SBmax – максимальный ход поршня; для центрального кривошипно -ползунного механизма: SBmax =2r1,
где r1- радиус кривошипа.
SB - фактическое перемещение поршня от крайнего положения до заданного в соответствии с происходящим в цилиндре процессом(всасывание, сжатие, нагнетание).
Pmax-максимальное давление воздуха в компрессоре.
Для построения индикаторной диаграммы в системе координат xy (рис.8) по оси x откладываем перемещение поршня SBmax ,которое делим на десять равных частей. По оси y в произвольном масштабе откладываем величину давления в цилиндре в MПа.
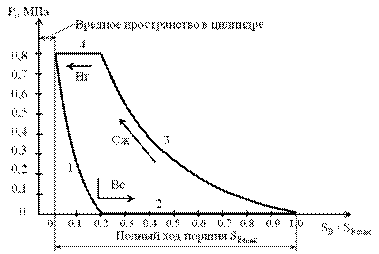
Рис.8 Индикаторная диаграмма работы компрессора
В соответствии с таблицей 1 при SB/SBmax=0, величина давления в цилиндре компрессора равна его максимальному значению; при SB/ SBmax=0,1давление в цилиндре Pi=0,3Pmax, а при SB/ SBmax=0,2 давление Pi=0. Отложив на графике полученные значения Pi получим кривую 1, характеризующую изменение давления оставшегося в цилиндре воздуха при движении поршня в режиме всасывания. Следует отметить, что давление оставшегося воздуха будет создавать движущую силу действующую в направлении движения поршня.
При дальнейшем движении поршня в цилиндре будет создаваться разряжение и произойдет всасывание воздуха (прямая 2).
На схеме механизма (рис.1) режим всасывания соответствует движению поршня 3 от точки В к точке O ,поршня 5 – от точки С к точке O.
При движении поршня в обратном направлении происходит сжатие воздуха в цилиндре. Величина давления изменяется в соответствии с кривой 3, построенной на основании данных таблицы 1. Так, например, перемещение поршня на одну десятую хода (от 1,0 до 0,9) увеличивает давление до Pi= 0,04Pmax, перемещение от 0,9 до 0,8 увеличивает давление до Pi= 0,08Pmax и т.д. Откладывая полученные таким образом значения давления воздуха в цилиндре на графике, получим кривую 3 (сжатие воздуха в цилиндре). Максимальное давление воздуха достигается при SB/ SBmax=0,2, после чего происходит его нагнетание в резервуар (линия 4).
Для определения величины давления Pi, соответствующей заданному положению кривошипа, с использованием индикаторной диаграммы необходимо определить соотношение SB/ SBmax для своего положения. Для этого на плане механизма или аналитически определяется фактический пройденный поршнем путь SB от его крайнего положения в соответствии с происходящим в компрессоре процессом (всасывание или нагнетание).
Например, для поршня 3 (рис.1) процесс сжатия начался, когда точка А была в положении 7, а полный ход соответствует повороту кривошипа из положения 7 в положение 1. Разделив величину перемещения поршня SB на величину полного хода поршня SBmax получим 0,9. При отсчете по кривой 3 справа налево (сжатие) найдем величину давления в цилиндре Pi, МПа, что позволяет определить силу Рс.
В результате в векторном уравнении (17) осталось две неизвестные величины R63 и R12n, что позволяет его решить графически. Для этого выбираем масштабный коэффициент построения плана сил KP1 [Н/мм], который показывает, сколько единиц силы содержится в одном миллиметре отрезка, изображающего вектор этой силы на чертеже. Величина масштабного коэффициента КР выбирается произвольно исходя из возможности размещения плана сил на имеющейся площади чертежа.
Разделив численные значения известных сил на выбранный масштабный коэффициент КР1 найдем величину отрезков-векторов, изображающих эти силы на чертеже.
Далее строим план сил (решаем уравнение (17) графически), откладывая последовательно отрезки-векторы сил на чертеже (рис.9), параллельно действующим силам. Для удобства определения реакции в точке В необходимо группировать силы, действующие на одно звено.
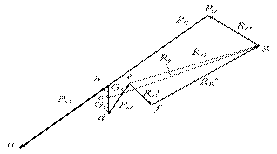
Рис.9 План сил для 1-ой группы Ассура
После построения плана сил определяем неизвестные силы:
R12n=КР1· fg [H]
R12=КР1· eg [H]
R63=КР1· Pf1g [H]
Для определения реакции в точке В замыкаем вектором RВ3 силы, действующие на звено 3, при этом так же замыкаются силы, действующие на звено 2, но направление вектора RВ2 изменяется на противоположное.
RВ=КР1· cg [H]
Аналогичным образом определяем силы и моменты, действующие на звенья структурной группы 4-5 (Рис.10).

Рис.10 Расчетная схема для 2-ой группы Ассура
Cилы тяжести:
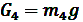 [Н]
[Н]
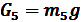 [Н]
[Н]
Силы инерции:
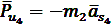 [Н]
[Н]
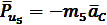 [Н]
[Н]
Момент сил инерции:
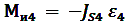 [Нм]
[Нм]
Момент инерции JS4 звена 4 равен моменту инерции JS2 звена 2.
Уравнение равновесие сил, действующих на звенья 4 и 5 в векторной форме:
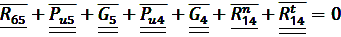 (19)
(19)
Рассматриваемая поршневая группа находится в фазе всасывания воздуха, поэтому при соотношении SС/SСmax≥ 0,2, согласно индикаторной диаграмме (рис.8), давление Рi, а, следовательно, и сила полезного сопротивления Рс равны 0. При выбранном положении кривошипа 1 (рис.1) SС/SСmax = 0,34, следовательно Рс = 0.
Для графического решения уравнения (19) определяем величину силы 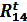 из уравнения моментов сил, действующих на звено 4 относительно точки C.
из уравнения моментов сил, действующих на звено 4 относительно точки C.
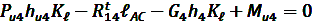
откуда находим:
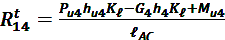 , [Н]
, [Н]
Выбрав масштаб плана сил КР2 и разделив на него численные значения сил, действующих на звенья группы 4-5, из полученных отрезков-векторов строим план сил (рис.11).
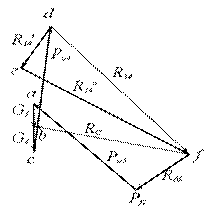
Рис.11 План сил для 2-ой группы Ассура
Определив с помощью плана сил величину отрезков-векторов неизвестных сил находим их величину:
R14n=КР2· ef [H]
R14=КР2· df [H]
R65=КР2· Pf2f [H]
Замыкая векторы сил, действующих на звено 4 (или 5) находим реакцию в точке C:
RС=КР2· bf [H]
На кривошип 1 в кинематических парах А1 и А2 действуют силы R21 и R41 соответственно, равные определенным ранее R12 и R14 и противоположные им по направлению.
Силы R21 и R41 создают момент сопротивления движению, поэтому для его преодоления к кривошипу необходимо приложить уравновешивающий момент Мур, равный по величине суммарному моменту от сил R21 и R41 и направленный в противоположную сторону (рис.12).

Рис.12 Схема моментов сил, действующих на кривошип
Для определения Мур составляем уравнение равновесия моментов всех сил относительно т.О (ΣМО=0):
Мур -R21h21Kℓ - R41h41Kℓ =0 ,
откуда Мур =R21h21Kℓ + R41h41Kℓ [Н м]
Кинетостатический расчет механизма обычно прозводится за полный цикл (в данном случае поворот кривошипа на 3600), в рамках которого для ряда положений механизма определяется величина Мур и строится график его изменения в зависимости от угла поворота кривошипа (рис.13).
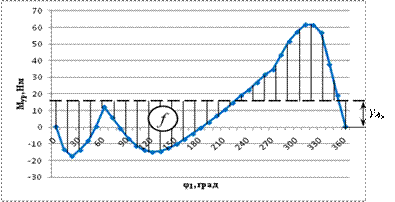
Рис.13 График изменения уравновешивающего момента
Площадьf под кривой [Мур, φ1]определяет работу, которую должен выполнять двигатель, приводящий механизм в движение. Ордината удв, равная высоте прямоугольника, площадь которого также равна f, соответствует в масштабе моменту двигателя:
Мдв = КМ удв, [Н м]
где КМ - масштабный коэффициент моментов.
Мощность двигателя на основе кинетостатического расчета можно определить по формуле:
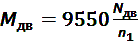 , (20)
, (20)
где n1- число оборотов кривошипа, мин-1;
Из формулы (20) следует:
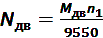 [КВт]
[КВт]
Минимальная мощность двигателя, необходимая для преодоления сил сопротивления в поршневых компрессора, определяется из граничного условия Мдв = Мур.
При силовом расчете механизма за цикл желательно построить годографы сил, действующих в кинематических парах.
Далее определяем силы, действующие на коленчатый вал (кривошип 1 на рис.1). Для этого расположим кривошип в системе координат ху (рис.14) и найдем проекции этих сил на оси.

Рис.14 Схема определения проекций сил R21 и R41
R21х = R21 cosα21 [H]
R21y = R21 sinα21 [H]
R41х = R41 cosα41 [H]
R41y = R41 sinα41 [H]
Для определения составляющих реакций углы α21 и α41 измеряются.
В рассматриваемом механизме кривошип представляет собой двухопорный вал, к колену которого присоединяются шатуны 2 и 4. Так как шатуны и поршни этого механизма движутся в параллельных плоскостях, реакции в подшипниках коленчатого вала определим из пространственной схемы (в осях xyz) действия на него составляющих сил R21 и R41 (рис.15). Реакции в подшипниках O1 и O2 представим в виде составляющих, направленных по осям координат.
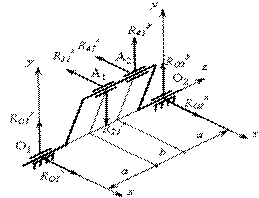
Рис.15 Расчетная схема для определения реакций в опорах коленчатого вала
Так как при силовом расчете неизвестны конструктивные размеры a и b коленчатого вала, задача решается в общем виде.
Для определения составляющей RO1х составляем уравнение равновесия моментов всех сил относительно оси О2у (ΣМО2у=0). При этом принимаем, что момент является положительным если со стороны положительного направления оси, относительно которой он реализуется, данный момент действует против часовой стрелки:
- R41ха - R21х(a+b) + RO1х(2a+b) = 0
откуда RO1х = (R21х(a+b) + R41ха) /(2a+b)
Если составляющая RO1х получается отрицательной, значит, ее необходимо перенаправить на расчетной схеме в противоположную сторону.
Аналогично составляем уравнения равновесия моментов сил для определения остальных неизвестных:
ΣМО2х=0: - R41уа + R21у(a+b) - RO1у(2a+b) = 0
ΣМО1у=0: R21хa +R41х(a+b) - RO2х(2a+b) = 0
ΣМО1х=0: - R21уa + R41у(a+b) + RO2у(2a+b) = 0
Величины реакций в подшипниках O1 и O2 находим по формулам:
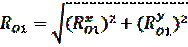
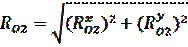
Векторы реакций RO1 и RO2 образуют с осью х углы γ1 и γ2, определяемые из соотношений:
cos γ1 = RO1х / RO1; cos γ2 = RO2х / RO2
