Упражнения для самостоятельной работы
9. Выполнить основные четыре действия алгебры над комплексными числами 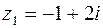 и
и 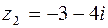 .
.
10. Найти действительные решения уравнения
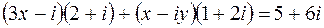 .
.
11. Найти середину отрезка, соединяющего точки 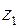 и
и 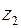 .
.
12. Три последовательные вершины параллелограмма находятся в точках 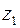 ,
, 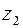 ,
, 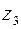 . Найти четвертую вершину.
. Найти четвертую вершину.
13. Показать, что 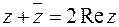 ,
, 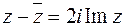 .
.
14. Изобразить на комплексной плоскости числа 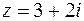 ,
, 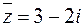 . Найти их модули и аргументы.
. Найти их модули и аргументы.
15. Изобразить на комплексной плоскости числа
а) 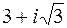 ; б)
; б) 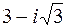 ; в)
; в) 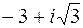 ;
;
г) 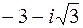 ; д)
; д) 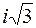 ; е)
; е) 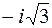
и вычислить их модули и главные значения аргумента.
16. Представить в показательной форме числа
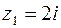 ;
; 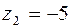 ;
; 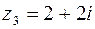 ;
; 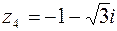 .
.
17. Найти модуль и аргумент числа 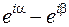 , если
, если 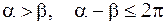 .
.
18. Вычислить 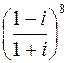 .
.
19. Решить уравнение 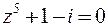 .
.
2. МНОЖЕСТВА ТОЧЕК, ЛИНИИ, ОБЛАСТИ
НА КОМПЛЕКСНОЙ ПЛОСКОСТИ
Линии и области на комплексной плоскости мы рассматриваем как множество точек, обладающих определенными свойствами и удовлетворяющих определенным уравнениям или системе уравнений, неравенствам или системе неравенств.
Параметрические уравнения кривой в действительных переменных
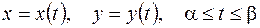
в комплексной плоскости могут быть заменены одним уравнением
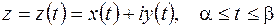 , (2.1)
, (2.1)
которое называется параметрическим или уравнением кривой в комплексной форме.
Если кривая задана в неявном виде 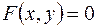 , то путем подстановки в это уравнение выражений
, то путем подстановки в это уравнение выражений
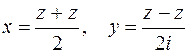 (2.2)
(2.2)
получим уравнение кривой в комплексной форме 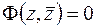 .
.
При решении задач по определению и изображению линии и областей в комплексной плоскости следует помнить геометрический смысл модуля разности двух комплексных чисел 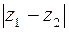 (см. упражнение 2). Рассматривая
(см. упражнение 2). Рассматривая 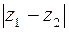 как расстояние между двумя точками
как расстояние между двумя точками 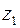 и
и 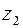 плоскости, достаточно легко задавать аналитически линии и области.
плоскости, достаточно легко задавать аналитически линии и области.
УПРАЖНЕНИЯ
20. Написать в комплексной форме уравнение кривой 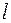 :
:
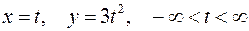 .
.
Решение. 1-й способ. Согласно (2.1) имеем параметрическое уравнение кривой 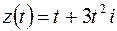 .
.
2-й способ. Легко видеть, что данная кривая – парабола 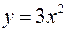 . Перейдем в этом уравнении к комплексному переменному, воспользовавшись формулами (2.2),
. Перейдем в этом уравнении к комплексному переменному, воспользовавшись формулами (2.2), 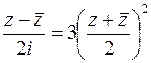 , откуда получаем
, откуда получаем 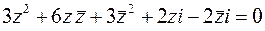 .
.
21. Написать уравнение окружности в комплексной форме.
Решение. 1-й способ. Рассмотрим окружность как множество точек  , равноудаленных на расстояние
, равноудаленных на расстояние 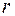 от центра
от центра 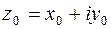 . Тогда имеем
. Тогда имеем 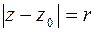 .
.
2-й способ. Как известно, параметрические уравнения окружности радиуса 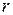 с центром в точке
с центром в точке 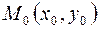 имеют вид
имеют вид
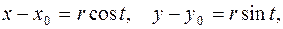 где
где 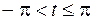 .
.
Следовательно, 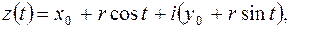
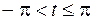 . Если воспользоваться показательной формой комплексного числа, то полученное уравнение можно записать в виде
. Если воспользоваться показательной формой комплексного числа, то полученное уравнение можно записать в виде 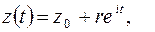
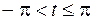 .
.
22. Написать уравнение эллипса с фокусами в точках 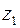 и
и 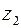 , большая ось которого равна
, большая ось которого равна 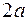 .
.
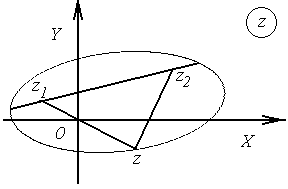 Рис.2.1 Рис.2.1 | Решение. По определению эллипса 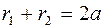 . Здесь . Здесь 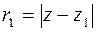 и и 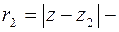 расстояния произ-вольной точки расстояния произ-вольной точки  эллипса до фокусов эллипса до фокусов 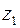 и и 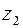 соответственно (рис.2.1). Следовательно, уравнение эллипса в комплексной форме имеет вид соответственно (рис.2.1). Следовательно, уравнение эллипса в комплексной форме имеет вид 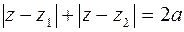 . . |
Расстояние между фокусами: 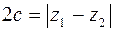 , а малая полуось по известным
, а малая полуось по известным 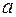 и
и 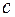 определяется из формулы
определяется из формулы 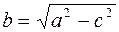 .
.
23. Выяснить геометрический смысл уравнения 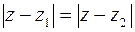 .
.
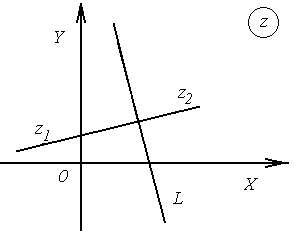 Рис.2.2 Рис.2.2 | Решение. 1-й способ геометрический. В данном случае 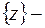 множество точек, равноудаленных от точек множество точек, равноудаленных от точек 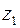 и и 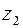 . Очевидно, это есть прямая . Очевидно, это есть прямая 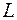 , перпендикулярная отрезку , перпендикулярная отрезку 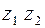 и проходящая через его середину (рис.2.2). и проходящая через его середину (рис.2.2). |
2-й способ аналитический. Пусть 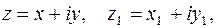
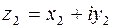 , тогда
, тогда
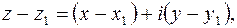
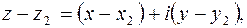
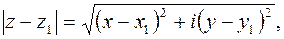
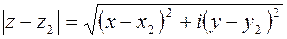 .
.
Поскольку левые части последних соотношений равны, то равны и их правые части, т.е. 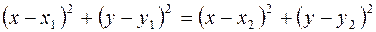 . После упрощения получаем уравнение прямой линии.
. После упрощения получаем уравнение прямой линии.
24. Какая кривая определяется уравнением 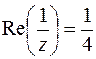 ?
?
Решение. Из области определения функции исключается точка 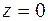 , пусть
, пусть 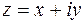 . Тогда
. Тогда 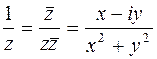 . Следовательно,
. Следовательно, 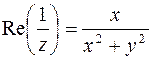 . По условию
. По условию 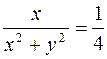 или
или 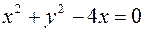 , откуда следует, что данное условие определяет окружность
, откуда следует, что данное условие определяет окружность 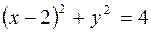 ,
, 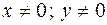 .
.
25. Определить, какое множество точек удовлетворяет условию 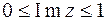 .
.
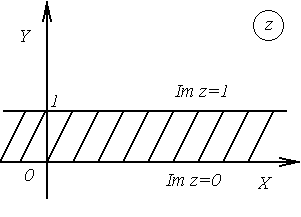 Рис.2.3 Рис.2.3 | Решение. Так как по определению 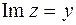 , то данное неравенство может быть записано в виде , то данное неравенство может быть записано в виде 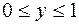 . Следовательно, искомое множество точек – полоса между прямыми . Следовательно, искомое множество точек – полоса между прямыми 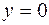 и и 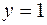 , включая эти прямые (рис. 2.3). , включая эти прямые (рис. 2.3). |
26. Построить на комплексной плоскости области, заданные условиями:
а) 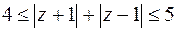 ; б)
; б) 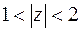 ,
, 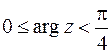 .
.
Решение. а) Искомое множество точек удовлетворяет двум неравенствам: 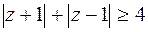 и
и 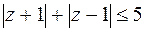 . Первое условие определяет точку эллипса с фокусами
. Первое условие определяет точку эллипса с фокусами 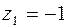 и
и 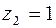 , для которого
, для которого 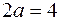 ,
, 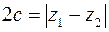 ,
, 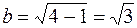 (уравнение эллипса в действительных переменных:
(уравнение эллипса в действительных переменных: 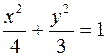 ). Второе уравнение – внутренность эллипса с фокусами в тех же точках с полуосями
). Второе уравнение – внутренность эллипса с фокусами в тех же точках с полуосями 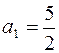 и
и 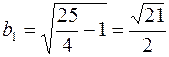 (уравнение эллипса в действительных переменных
(уравнение эллипса в действительных переменных 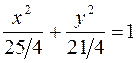 ).
).
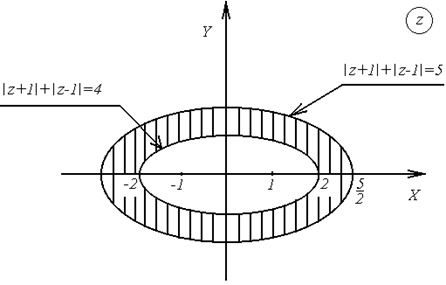 Рис.2.4 Рис.2.4 | Искомое множество точек – часть плоскости, заключенная между двумя эллипсами (рис. 2.4), включая сами эллипсы. |
б) Легко видеть, что множество точек, удовлетворяющих условию 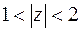 , есть внутренность кольца, ограниченного окружностями
, есть внутренность кольца, ограниченного окружностями 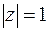 и
и 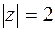 с центрами в начале координат и радиусами 1 и 2. Система неравенств
с центрами в начале координат и радиусами 1 и 2. Система неравенств 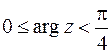 определяет множество точек, составляющих угол между лучами
определяет множество точек, составляющих угол между лучами 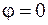 и
и 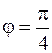 , причем точки первого луча принадлежат области, а второго – нет.
, причем точки первого луча принадлежат области, а второго – нет.
Пересечение указанных множеств определяет искомую область 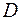 , которая изображена на рис. 2.5.
, которая изображена на рис. 2.5.
27. Какое множество точек комплексной плоскости определяется условием 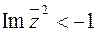 ?
?
Решение. Пусть 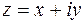 . Тогда
. Тогда 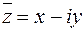 и
и 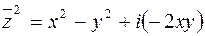 . Следовательно,
. Следовательно, 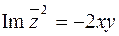 . По условию
. По условию 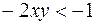 или
или 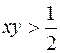 . Полученное неравенство определяет множество точек, изображенных на рис. 2.6.
. Полученное неравенство определяет множество точек, изображенных на рис. 2.6.
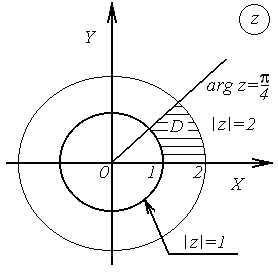 Рис.2.5 Рис.2.5 | 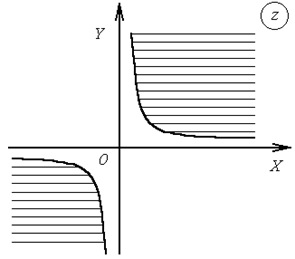 Рис.2.6 Рис.2.6 |
