Законы Кирхгофа в операторной форме
Некоторые свойства изображений
- Изображение суммы функций равно сумме изображений слагаемых:
.
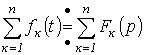- При умножении оригинала на коэффициент на тот же коэффициент умножается изображение:
.
С использованием этих свойств и данных табл. 1, можно показать, например, что
.
Изображения производной и интеграла
В курсе математики доказывается, что если 
, то 
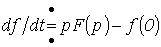, где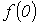 
- начальное значение функции 
.
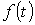Таким образом, для напряжения на индуктивном элементе можно записать
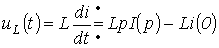
или при нулевых начальных условиях
.
Отсюда операторное сопротивление катушки индуктивности
.
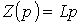Аналогично для интеграла: если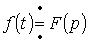 
, то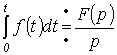 
.
С учетом ненулевых начальных условий для напряжения на конденсаторе можно записать:
.
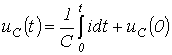Тогда
или при нулевых начальных условиях
,
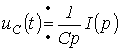откуда операторное сопротивление конденсатора
.
Закон Ома в операторной форме
Пусть имеем некоторую ветвь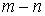 
(см. рис. 1), выделенную из некоторой
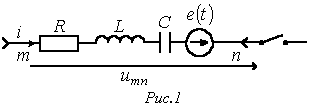
сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые.
Для мгновенных значений переменных можно записать:
.
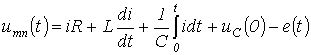Тогда на основании приведенных выше соотношений получим:
.
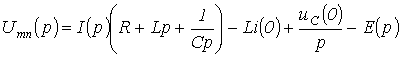Отсюда
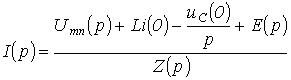 , | (2) |
где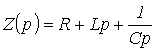 
- операторное сопротивление рассматриваемого участка цепи.
Следует обратить внимание, что операторное сопротивление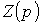 
соответствует комплексному сопротивлению 
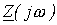ветви в цепи синусоидального тока при замене оператора р на 
.
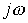Уравнение (2) есть математическая запись закона Ома для участка цепи с источником ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать операторную схему замещения,представленную на рис. 2.
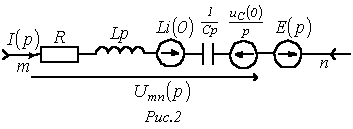
Законы Кирхгофа в операторной форме
Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю
.
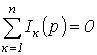Второй закон Кирхгофа:алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура
.
При записи уравнений по второму закону Кирхгофа следует помнить о необходимости учета ненулевых начальных условий (если они имеют место). С их учетом последнее соотношение может быть переписано в развернутом виде
.
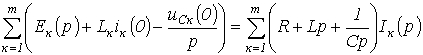В качестве примера запишем выражение для изображений токов в цепи на рис. 3 для двух случаев: 1 - 
; 2 -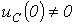 
.
В первом случае в соответствии с законом Ома 
.
Тогда
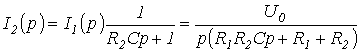
и
.
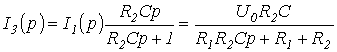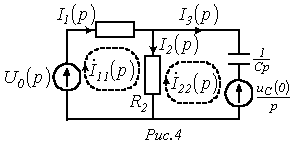
Во втором случае, т.е. при 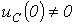, для цепи на рис. 3 следует составить операторную схему замещения, которая приведена на рис. 4. Изображения токов в ней могут быть определены любым методом расчета линейных цепей, например, методом контурных токов:
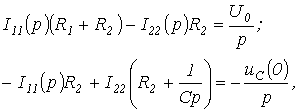
откуда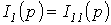 
; 
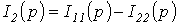и 
.