Символический метод расчета цепей синусоидального тока
Сущность метода состоит в том, что для упрощения расчета цепей синусоидального тока переходят от уравнений для мгновенных значений, являющихся по сути интегро-дифференциальными уравнениями, к алгебраическим уравнениям в комплексной форме. Расчет цепи удобнее вести для комплексных действующих величин синусоидальных токов и напряжений.
Для схемы (рис. 1) c входным напряжением  заданы следующие параметры:
заданы следующие параметры:

r1 = 4,5 Ом; r2 = 5 Ом;
r3 = 2,7 Ом; xL1 = j3 Ом;
xC2 = -j1,5 Ом; xC3 = -j4,5 Ом; xL4 = j3,5 Ом;
Е = 14,76 В; jЕ = 54,4°.
Рис. 1
Для заданной схемы определить токи в ветвях, падения напряжений на каждом элементе цепи, рассчитать баланс активных и реактивных мощностей и построить в масштабе векторно-топографическую диаграмму.
Порядок расчета:
1. Определяем комплексные сопротивления каждой ветви
 Ом,
Ом,
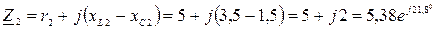 Ом,
Ом,
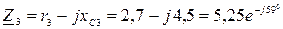 Ом.
Ом.
2. Определяем комплексное сопротивление разветвленного участка Zab: 
3. Определяем комплексное сопротивление всей цепи ZΣ:
ZΣ =Z1 + Zab = 4,5 + j3 + 3,29 – j1,13 = 7,79 + j1,87 = 7,95e j13,6 Ом.
4. Записываем напряжение источника в комплексной форме Е и определяем ток I1в неразветвленной части цепи:
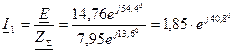 = 1,4 + j1,2 A.
= 1,4 + j1,2 A.
5. Определяем напряжение на разветвленном участке «ав»:
Uab= I1×Zab=  ×3,48e -j19° =6,46e j21,8° =(6+ j2,4) В.
×3,48e -j19° =6,46e j21,8° =(6+ j2,4) В.
6. Определяем токи в остальных ветвях:
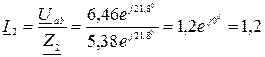 A;
A;
 A.
A.
7. Мгновенное значение тока i3 определяем по его комплексному действующему значению I3 =1,23e j80,8ْ А.
Комплексная амплитуда тока Im3 = 
 =
=  ×1,23e j80,8ْ B,
×1,23e j80,8ْ B,
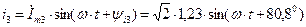 А.
А.
8. Комплексную мощность всей цепи определяем как
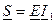 = P ± jQ,
= P ± jQ,
где Е =14,76e j54,4ْ = 8,59 +j12 В, I1 =1,85e -j40,8 А,
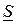 =14,76e j54,4ْ ×1,85e -j40,8ْ =27,3e j13,6 = (26,5+ j6,4)ВА.
=14,76e j54,4ْ ×1,85e -j40,8ْ =27,3e j13,6 = (26,5+ j6,4)ВА.
9. Согласно закону сохранения энергии активная мощность всей цепи равна сумме активных мощностей всех n активных сопротивлений, входящих в цепь: 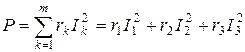 =4,5×1,852+5×1,22+2,7×1,232=26,52 Вт.
=4,5×1,852+5×1,22+2,7×1,232=26,52 Вт.
10. По закону сохранения энергии реактивная мощность всей цепи равна алгебраической сумме мощностей всех m реактивных сопротивлений, входящих в цепь (Xk >0, если сопротивление индуктивное и Xk <0, если емкостное): 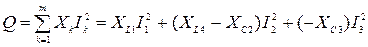 =
=
= 3×1,852 + (3,5-1,5)×1,22 + (-4,5)×1,232 = 6,43 ВAp.
Баланс активных и реактивных мощностей сходится:
P = 26,5 ≈ 26,52Вт; Q = 6,4 ≈ 6,43 ВAp.
11. Топографическая диаграмма — это векторная диаграмма цепи, в которой каждой точке электрической схемы соответствует точка на топографической диаграмме (рис. 2).
Это достигается тем, что векторы напряжений на отдельных элементах схемы строятся в той последовательности, в которой они расположены в схеме (обходим схему в направлении тока – по часовой стрелке).
Для построения топографической диаграммы определяем напряжения на всех элементах цепи.
Ur1 = I1 R1 = 1,85e -j40,8°×4,5 = 8,34e -j40,8° = 6,31 – j5,45 В;
UL1 = I1 XL1 = 1,85e -j40,8°×3e j90° = 5,55e j49,2° = 3,63 + j4,2 В;
Ur2 = I2 R2 = 1,2 ×5 = 6 В;
UС2 = I2 XС2 = 1,2 × 1,5 e -j90° = 1,8 e –j90° = –j1,8 В;
UL2 = I2 XL2 = 1,2 ×3,5e j90° = 4,2 e j90° = j4,2 В;
Ur3 = I3 r3 = 1,23 × 2,7 = 3,32 В;
UC3 = I3 X3 = 1,23 × 4,5 = 5,54 В.
12. Проводим проверку правильности расчета токов и напряжений по 1 и 2 законам Кирхгофа, используя алгебраическую форму записи комплексных чисел.
Проверка по 1 закону осуществляется для любого из двух узлов а или в. Например, для узла а:
I1 – I2 – I3 = 0, значит I1 = I2 + I3,
следовательно, 1,4 + j1,2 = 1,2 + 0,2 + j1,21 » 1,4 + j1,21.
Аналогично проводим проверку по 2 закону для контура а в с, обходя его по часовой стрелке
E = Ur2 + UL2 + UC2 + Ur1 + UL1.
8,59 +j12 = 6,31 – j5,45 + 3,63 + j4,2 + 6 + j4,2 – j1,8.
Если результаты проверок удовлетворительные, то можно строить векторную диаграмму.
13. Выбираем масштабы по току и напряжению μI = 0,1 А/мм, μU = 1 В/мм. Построение топографической векторной диаграммы начинаем с построения векторов токов, которые проводим из начала координат под углами, найденными в П4 и П6. Диагональ параллелограмма должна соответствовать вектору 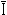 1=
1= 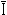 2+
2+ 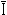 3.
3.
Из начала координат под углом Ψu = -54,4° строим вектор питающего напряжения Е. Затем так же из начала координат (точка а) по направлению тока I2 строим сначала вектор падения напряжения Ur2, а затем последовательно вектора UL2 и UС2, ориентируя их соответствующим образом относительно тока I2. Построение векторов Ur1 и UL1 ориентируем относительно тока I1. Векторная сумма этих последовательно построенных пяти падений напряжений, согласно 2 закону Кирхгофа, равна вектору питающего напряжения Е.
Аналогичным образом строим сумму векторов падений напряжений Ur3 и UC3, ориентируя их по току третьей ветви I3.
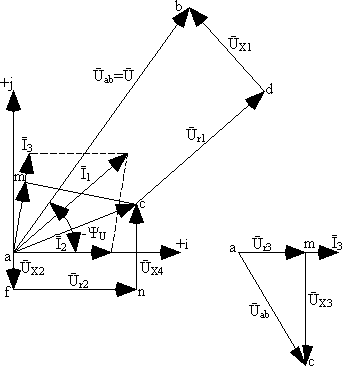
Рис. 2
