Расчет закрытой цилиндрической зубчатой передачи
Кинематический расчет
Определим вращающие моменты на валах.
Угловая частота вращения вала:
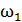 =
= 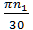 =
= 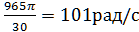 [1; с.46]
[1; с.46]
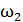 =
= 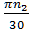 =
= 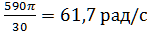
Вращающий момент на валах привода, Нм:
Т= 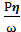 , где P- мощность, Вт [1; с.46]
, где P- мощность, Вт [1; с.46]
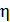 = 0,95 – КПД цилиндрической закрытой передачи.
= 0,95 – КПД цилиндрической закрытой передачи.
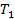 =
= 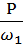 =6500/101=64,35 – Вращающий момент на ведущем валу;
=6500/101=64,35 – Вращающий момент на ведущем валу;
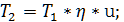 где
где 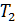 – вращающий момент на ведомом валу;
– вращающий момент на ведомом валу;
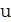 - передаточное отношение;
- передаточное отношение; 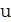 =
= 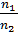 =
= 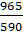 = 1,63
= 1,63
 =0,95 –КПД;
=0,95 –КПД;
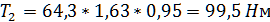
 |
2. Выбор материала и термообработки зубчатых колес
Сталь в настоящее время – это основной материал для изготовления зубчатых колес. Одним из важных условий является повышение контактной прочности поверхностей зубьев и их прочности на изгиб. При этом снижаются габаритные размеры.
Сочетание шестерни, закаленной при нагреве ТВЧ, и улучшенного колеса дает большую нагрузочную способность. Такая пара хорошо прирабатывается, ее применение предпочтительно.
Поэтому выбираем материал 40ХН. Для шестерни термообработку – закалка ТВЧ до твердости зубьев 48…53 HRC, для колеса улучшение до твердости 269…302HB.
 |
Допускаемые напряжения
3.1 Определение допускаемых контактных напряжений
Допускаемые контактные напряжения определяются по формуле:
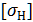 =
= 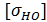 *
* 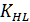 ; [1;с55]
; [1;с55]
Где 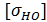 - базовое допускаемое напряжение, МПа;
- базовое допускаемое напряжение, МПа;
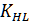 -коэффициент долговечности;
-коэффициент долговечности;
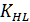 =1- при длительной работе привода.
=1- при длительной работе привода.
Шестерня:
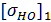 =14HRC+170=14
=14HRC+170=14 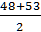 +170=877МПа; [1;табл3.1]
+170=877МПа; [1;табл3.1]
Колесо: 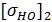 =1,8HB+67=1,8
=1,8HB+67=1,8 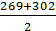 +67=580МПа;
+67=580МПа;
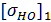 =877*1=877МПа
=877*1=877МПа
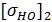 =580*1=580МПа
=580*1=580МПа
Зубчатые передачи рассчитывают по меньшему значению из полученных для шестерни и колеса, то есть принимаем: 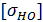 =580МПа.
=580МПа.
3.2 Определение допускаемых напряжений изгиба
Определяется отдельно для шестерни и колеса:
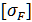 =
= 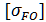 *
* 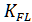 , где [1; с56]
, где [1; с56]
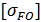 - предел выносливости при изгибе, МПа
- предел выносливости при изгибе, МПа
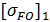 =370МПа- при закалке [1;табл3.1]
=370МПа- при закалке [1;табл3.1]
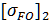 =1,03HB=
=1,03HB= 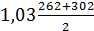 =294МПа
=294МПа
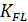 - коэффициент долговечности;
- коэффициент долговечности;
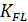 =1 - при длительной нагрузке.
=1 - при длительной нагрузке.
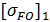 =370*1=370 МПа
=370*1=370 МПа
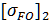 =294 *1=294 МПа.
=294 *1=294 МПа.
 |
4. Выбор вида передачи
Прямозубые передачи применяют в основном при невысоких скоростях, в планетарных и открытых передачах. Косозубые колеса применяют для ответственных передач при средних и высоких скоростях. Косозубые передачи обладают меньшим шумом и большей плавностью при работе. Поэтому я применяю косозубую передачу.
 |
Расчет закрытой цилиндрической зубчатой передачи
5.1 Проектный расчёт
5.1.1. Определение межосевого расстояния
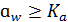 *(u+1)
*(u+1) 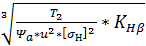 ; [1; с61]
; [1; с61]
Где 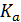 - вспомогательный коэффициент
- вспомогательный коэффициент
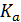 =430-для косозубых передач;
=430-для косозубых передач;
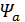 –коэффициент ширины венца колеса
–коэффициент ширины венца колеса
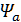 =0,3-для шестерни, расположенной симметрично относительно опор в проектируемых нестандартных одноступенчатых цилиндрических редукторах;
=0,3-для шестерни, расположенной симметрично относительно опор в проектируемых нестандартных одноступенчатых цилиндрических редукторах;
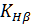 -коэффициент неравномерности нагрузки;
-коэффициент неравномерности нагрузки;
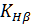 =1- для прирабатывающихся колес;
=1- для прирабатывающихся колес;
u- передаточное число =1,63
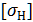 – допускаемое контактное напряжение, равное 580 МПа (п.3.1 ПЗ)
– допускаемое контактное напряжение, равное 580 МПа (п.3.1 ПЗ)
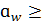 430*(1,63+1)
430*(1,63+1) 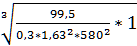 =83,46 мм
=83,46 мм
Округляем межосевое расстояние до 80мм.
 |
5.1.2.Определение модуля зацепления
m 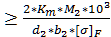 [1; с.62]
[1; с.62]
где 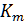 - вспомогательный коэффициент, для косозубой передачи =5,8;
- вспомогательный коэффициент, для косозубой передачи =5,8;
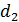 - делительный диаметр колеса, мм;
- делительный диаметр колеса, мм;
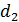 =
= 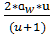 =
= 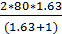 =99мм.
=99мм.
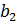 -ширина венца колеса, мм;
-ширина венца колеса, мм;
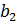 =
= 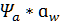 =0,3*80=24мм.
=0,3*80=24мм.
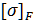 –допускаемое напряжение изгиба материала колеса с менее прочным зубом, Н/
–допускаемое напряжение изгиба материала колеса с менее прочным зубом, Н/ 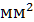 =294.
=294.
m 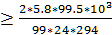 =1,65мм
=1,65мм
Округлим до значения из стандартного ряда до m=2 (по табл. с.62)
5.1.3. Определение угла наклона зубьев
 = arcsin
= arcsin 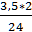 = 16, 95° [1; с.62]
= 16, 95° [1; с.62]
В косозубых передачах угол наклона зубьев принимают β=8…16.
При больших β у косозубых зубчатых передач возрастает осевая сила.
5.1.4.Определение суммарного числа зубьев
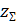 =
= 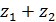 =
= 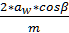 =
= 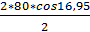 =76,5 [1; с.62]
=76,5 [1; с.62]
Полученное значение zΣ округлим до целого числа 77.
 |
5.1.5. Уточним действительную величину угла наклона зубьев для косозубых передач:
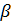 =arccos [(zΣ * m)/(2* aw)]= arccos (0,9625) = 15,74°= 15° 40!
=arccos [(zΣ * m)/(2* aw)]= arccos (0,9625) = 15,74°= 15° 40!
5.1.6. Определение числа зубьев шестерни:
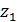 =
= 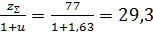 [1; с.62]
[1; с.62]
Из условий уменьшения шума и отсутствия подрезания зубьев рекомендуется 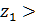 18.
18.
Принимаем z1= 29 зубьев.
5.1.7. Определение числа зубьев шестерни:
Z2= ZΣ– Z1 = 77-29 =48 зубьев
5.1.8. Определение фактического передаточного числа
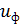 =
= 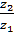 =
=  =1,655 [1; с.62]
=1,655 [1; с.62]
Необходимо проверить его отклонение от заданного
∆u= 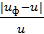 *100% =[(1,655-1,63)/1,63]*100% = 1,5%
*100% =[(1,655-1,63)/1,63]*100% = 1,5% 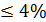 [1; с.63]
[1; с.63]
5.1.9. Определение фактического межосевого расстояния
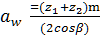 =
= 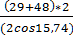 = 80 мм
= 80 мм
5.1.10. Определение геометрических параметров зубчатых колес:
делительные диаметры:
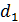 =
= 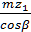 =
= 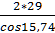 =60, 26 мм
=60, 26 мм
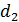 =
= 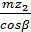 =
= 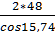 = 99, 74 мм
= 99, 74 мм
 диаметры вершин зубьев:
диаметры вершин зубьев:
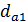 =
= 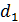 +2m = 60,26+2*2=64, 26 мм
+2m = 60,26+2*2=64, 26 мм
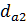 =
= 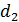 +2m = 99,74+2*2 =103, 74 мм
+2m = 99,74+2*2 =103, 74 мм
диаметры впадин:
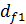 =
= 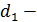 2,4m = 60,26
2,4m = 60,26 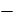 2,4*2= 60,26–4,8=55,46 мм
2,4*2= 60,26–4,8=55,46 мм
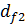 =
= 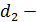 2,4m =99,74
2,4m =99,74 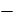 2,4*2= 99,74–4.8 =94,94 мм
2,4*2= 99,74–4.8 =94,94 мм
ширина венца шестерни:
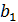 =
= 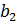 +2…5=24+4=28 мм
+2…5=24+4=28 мм
5.2. Проверочный расчет
5.2.1. Проверим межосевое расстояние
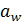 =
=  =
= 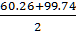 = 80 мм
= 80 мм
5.2.2.Проверим пригодность заготовок
Для стали 40ХН заготовка 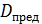 =200мм
=200мм 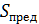 =125 мм
=125 мм
Следовательно, возможно изготовить поковку для проектируемого зубчатого колеса.
5.2.3. Проверим контактные напряжения
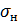 =K
=K 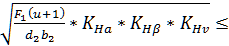 [
[ 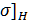 [1; с.64]
[1; с.64]
Где К- вспомогательный коэффициент;
К= 376 - для косозубой передачи;
Ft- окружная сила в зацеплении, Н; 
Ft = 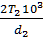 =
= 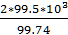 = 1995 H
= 1995 H
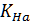 - коэффициент, учитывающий распределение нагрузки между зубьями, зависит от окружной скорости и степени точности передачи:
- коэффициент, учитывающий распределение нагрузки между зубьями, зависит от окружной скорости и степени точности передачи:
Окружная скорость : 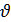 =
= 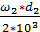 =
= 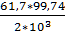 = 3, 077 м/с
= 3, 077 м/с
Принимаем 8 степень точности передачи по ГОСТ 1643-81.
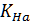 =1,08- при окружной скорости 3м/с и 8 степени точности; [1; рис.4.2]
=1,08- при окружной скорости 3м/с и 8 степени точности; [1; рис.4.2]
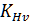 –коэффициент динамической нагрузки;
–коэффициент динамической нагрузки;
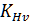 =1,04-при окружной скорости 3 м/с и 8 степени точности; [1; табл.4.3]
=1,04-при окружной скорости 3 м/с и 8 степени точности; [1; табл.4.3]
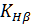 - коэффициент неравномерности нагрузки;
- коэффициент неравномерности нагрузки;
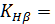 1- для прирабатывающихся колес.
1- для прирабатывающихся колес.
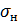 = 376* {[1995*(1,65+1)/ (99,74*24)]*1,08*1,04*1 }1/2 =376*1,57 = 590 МПа это больше, чем допускаемое =580 МПа,
= 376* {[1995*(1,65+1)/ (99,74*24)]*1,08*1,04*1 }1/2 =376*1,57 = 590 МПа это больше, чем допускаемое =580 МПа,
Условие прочности не выполнено, следовательно, меняем b2 на
b2=30 мм
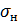 =376* {[1995*(1,65+1)/ (99,74*30)]*1,08*1,04*1 }1/2=376*1,4= 526,4 МПа теперь условие прочности выполнено.
=376* {[1995*(1,65+1)/ (99,74*30)]*1,08*1,04*1 }1/2=376*1,4= 526,4 МПа теперь условие прочности выполнено.
5.2.4. Проверим напряжения изгиба зубьев
Проверку выполним отдельно для шестерни и колеса, H/ 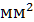 :
:
ϬF= 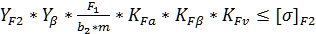 [1; с. 65]
[1; с. 65]
Где 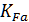 – коэффициент, учитывающий распределение нагрузки между зубьями, зависит от степени точности передачи
– коэффициент, учитывающий распределение нагрузки между зубьями, зависит от степени точности передачи
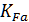 = 0,91 при степени точности 8; [1; с.66]
= 0,91 при степени точности 8; [1; с.66]
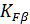 - коэффициент неравномерности нагрузки по длине зуба;
- коэффициент неравномерности нагрузки по длине зуба;
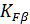 =1 – для прирабатывающихся зубьев колес;
=1 – для прирабатывающихся зубьев колес; 
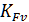 - коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи;
- коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи;
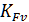 = 1,11 – при 8 степени точности и окружной скорости 3 м/с;
= 1,11 – при 8 степени точности и окружной скорости 3 м/с;
[1; табл. 4.3]
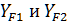 – коэффициенты формы зуба шестерни и колеса.
– коэффициенты формы зуба шестерни и колеса.
Определяются по таблице в зависимости от числа зубьев шестерни 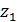 и колеса
и колеса 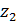 .
.
Для косозубых – в зависимости от эквивалентного числа зубьев шестерни
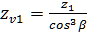 =
= 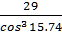 = 32
= 32
Принимаем 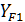 = 3,78
= 3,78
Колеса
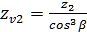 =
= 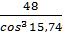 = 54
= 54
Принимаем 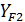 = 3, 64
= 3, 64
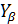 - коэффициент, учитывающий наклон зуба;
- коэффициент, учитывающий наклон зуба;
Для косозубых колес:
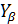 = 1-
= 1- 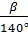 = 1
= 1 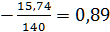
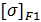 и
и 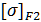 – допускаемые напряжения изгиба шестерни и колеса, Н/
– допускаемые напряжения изгиба шестерни и колеса, Н/ 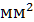 .
.
Итак, рабочие напряжения
ϬF2 =3,64*0,89*(1995/2*30)*0,9*1*1,11=3,2 * 33,25 *0,999=106,3 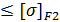 = 294 МПа
= 294 МПа
ϬF1= ϬF2*Y F1/ Y F2 =106,3*3,78/3,64= 110,4 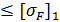 =370 МПа
=370 МПа
Условие прочности выполнено.
 |
