Способы задания плоскости на чертеже. Главные линии плоскости

Множество элементов плоскости изобразить на чертеже нельзя. Поэтому плоскость принято изображать геометрическими элементами, лежащими в плоскости.

Задание плоскости тремя точками.
Три точки, не лежащие на одной прямой, задают плоскость (рис.3.6а). Любая четвертая, пятая и т.д. точки, взятые произвольно на чертеже, как правило, не принадлежат заданной плоскости. Определитель: (A, B, C).

Рис. 3.6-a Рис. 3.6-б

Задание плоскости прямой и точкой вне этой прямой.
Если две точки плоскости соединить прямой, то получим задание плоскости прямой и точкой (рис.3.6-б). Всякий дополнительный элемент (точка, прямая), взятый произвольно, как правило, не будет принадлежать этой плоскости. Определитель: (A, b)[Ab].

Задание плоскости двумя пересекающимися прямыми.
Две пересекающиеся прямые определяют плоскость (рис.3.6-в). Определитель: (A, b)[Ab].

В ряде случаев плоскость удобно задавать двумя пересекающимися прямыми уровня: горизонталью и фронталью (рис.3.6-г).

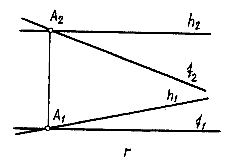Рис. 3.6-в Рис. 3.6-г

Задание плоскости двумя параллельными прямыми.
Так как параллельные прямые можно рассматривать как пересекающиеся в несобственной точке, то они также будут определять плоскость (рис.3.6-д). Определитель: (ab).

Задание плоскости плоской фигурой (отсек плоскости).
Любая плоская фигура, например треугольник, задает плоскость (рис.3.6-е). Плоская фигура придает большую наглядность изображаемой плоскости. Определитель: (ABC).

Рис. 3.6-д 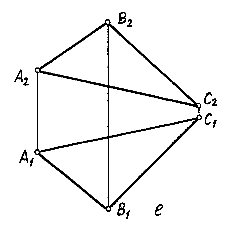Рис. 3.6-е

Необходимо отметить, что при всех случаях задания плоскость считается бесконечной.

Главные линии плоскости это линии уровня (горизонталь и фронталь) и линия наибольшего наклона (линия ската).Фронтали – прямые линии, лежащие в плоскости и параллельные фронтальной плоскости проекций. Горизонтали -прямые линии, лежащие в плоскости и параллельные горизонтальной плоскости проекций. Линии наибольшего наклона (ската) – прямые линии, лежащие в плоскости и перпендикулярные горизонтали этой плоскости.

Вопрос Плоскость общего положения и ее проекции

Плоскость общего положения.Плоскость а, наклонная ко всем плоскостям проекций, называется плоскостью общего положения (фиг.223,а).

Особенностью этой плоскости является то, что всякая кривая и фигура, лежащие в этой плоскости, при проектировании не имеют ни одной проекции, равной натуральной (истинной) величине. Все ее следы k, L и m наклонены к осям х, z и у, замыкаясь, образуют фигуру треугольника, называемого треугольником следов. Такую плоскость можно изображать проекциями ее следов.