Понятие алгебраической линии и её порядка
Линию на плоскости называют алгебраической, если в аффинной системе координат её уравнение имеет вид 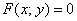 , где
, где 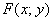 – многочлен, состоящий из слагаемых вида
– многочлен, состоящий из слагаемых вида 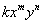 (
( 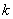 – действительное число,
– действительное число, 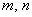 – целые неотрицательные числа).
– целые неотрицательные числа).
Как видите, уравнение алгебраической линии не содержит синусов, косинусов, логарифмов и прочего функционального бомонда. Только «иксы» и «игреки» в целых неотрицательныхстепенях.
Далее под словом «линия» по умолчанию будет подразумеваться алгебраическая линия на плоскости
Порядок линии равен максимальному значению 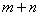 входящих в него слагаемых.
входящих в него слагаемых.
По соответствующей теореме, понятие алгебраической линии, а также её порядок не зависят от выбора аффинной системы координат, поэтому для лёгкости бытия считаем, что все последующие выкладки имеют место быть в декартовых координатах 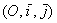 .
.
Общее уравнение линии второго порядка имеет вид 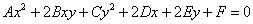 , где
, где 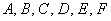 – произвольные действительные числа (
– произвольные действительные числа ( 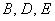 принято записывать с множителем-«двойкой»), причём коэффициенты
принято записывать с множителем-«двойкой»), причём коэффициенты 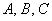 не равны одновременно нулю.
не равны одновременно нулю.
Если 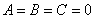 , то уравнение упрощается до
, то уравнение упрощается до 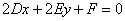 , и если коэффициенты
, и если коэффициенты 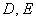 одновременно не равны нулю, то это в точности общее уравнение «плоской» прямой, которая представляет собой линию первого порядка.
одновременно не равны нулю, то это в точности общее уравнение «плоской» прямой, которая представляет собой линию первого порядка.
Многие поняли смысл новых терминов, но, тем не менее, в целях 100%-го усвоения материала сунем пальцы в розетку. Чтобы определить порядок линии, нужно перебратьвсе слагаемые её уравнения и у каждого из них найти сумму степеней входящих переменных.
Например:
слагаемое 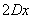 содержит «икс» в 1-ой степени;
содержит «икс» в 1-ой степени;
слагаемое 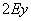 содержит «игрек» в 1-ой степени;
содержит «игрек» в 1-ой степени;
в слагаемом 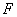 переменные отсутствуют, поэтому сумма их степеней равна нулю.
переменные отсутствуют, поэтому сумма их степеней равна нулю.
Далее из полученных чисел выбирается максимальное значение, в данном случае единица, – это и есть порядок линии.
Теперь разберёмся, почему уравнение 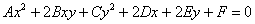 задаёт линию второго порядка:
задаёт линию второго порядка:
слагаемое 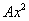 содержит «икс» во 2-ой степени;
содержит «икс» во 2-ой степени;
у слагаемого 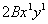 сумма степеней переменных: 1 + 1 = 2;
сумма степеней переменных: 1 + 1 = 2;
слагаемое 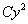 содержит «игрек» во 2-ой степени;
содержит «игрек» во 2-ой степени;
все остальные слагаемые – меньшей степени.
Максимальное значение: 2
Если к нашему уравнению дополнительно приплюсовать, скажем, 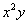 , то оно уже будет определять линию третьего порядка. Очевидно, что общий вид уравнения линии 3-го порядка содержит «полный комплект» слагаемых, сумма степеней переменных в которых равна трём:
, то оно уже будет определять линию третьего порядка. Очевидно, что общий вид уравнения линии 3-го порядка содержит «полный комплект» слагаемых, сумма степеней переменных в которых равна трём:
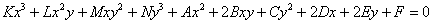 , где коэффициенты
, где коэффициенты 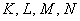 не равны одновременно нулю.
не равны одновременно нулю.
В том случае, если добавить одно или несколько подходящих слагаемых, которые содержат 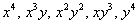 , то речь уже зайдёт о линии 4-го порядка, и т.д.
, то речь уже зайдёт о линии 4-го порядка, и т.д.
С алгебраическими линиями 3-го, 4-го и более высоких порядков нам придется столкнуться ещё не раз, в частности, при знакомстве с полярной системой координат.
Однако вернёмся к общему уравнению 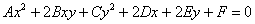 и вспомним его простейшие школьные вариации. В качестве примеров напрашивается парабола
и вспомним его простейшие школьные вариации. В качестве примеров напрашивается парабола 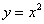 , уравнение которой легко привести к общему виду
, уравнение которой легко привести к общему виду 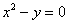 , и гипербола
, и гипербола 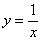 с эквивалентным уравнением
с эквивалентным уравнением 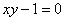 . Однако не всё так гладко….
. Однако не всё так гладко….
Существенный недостаток общего уравнения состоит в том, что почти всегда не понятно, какую линию оно задаёт. Даже в простейшем случае 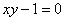 не сразу сообразишь, что это гипербола. Такие расклады хороши только на маскараде, поэтому в курсе аналитической геометрии рассматривается типовая задача приведения уравнения линии 2-го порядка к каноническому виду.
не сразу сообразишь, что это гипербола. Такие расклады хороши только на маскараде, поэтому в курсе аналитической геометрии рассматривается типовая задача приведения уравнения линии 2-го порядка к каноническому виду.
