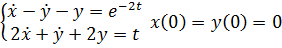Примеры решения творческих задач
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К изучению темы
Операционное исчисление
Для студентов всех специальностей

ЕГФ
Таганрог 1994
Составители: С.И. Александрийская, Б.И. Алексанрдийский,
М.П. Бородицкий, Э.А. Земскова
УДК 517.432 (0.7 07)
Методические указания к изучению темы «Операционное исчесление»/ Таганрог. гос.радиотехн. ун-т; С.И. Александрийская, Б.И. Александрийский, М.П. Бородицкий, Э.А. Земскова, Таганрог, 1994. 24с.
Настоящие методические указания предназначены для студентов всех специальностей ЕГФ. В них приводятся краткие теоретические сведения, формулы соответствия, указания к решению задач и решения типовых задач, образцы решения задач творческого рейтинга. Кроме того, дан минимум задач по теме примерные варианты контрольных работ.
Табл. 1. Библиогр.: 6 назв.
Рецензент Е.А. Иванов, канд. физ-мат. наук; доцент кафедры высшей математики ТРТУ.
Методические указания
1.1 Преобразование Лапласа и его свойства
Функцией-оригиналом будем называть любую комплексозначную функцию 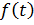 действительного аргумента
действительного аргумента  , удовлетворяющую следующим условиям:
, удовлетворяющую следующим условиям:
1) 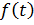 непрерывна вместе со своими производными достаточно высокого порядка на всей оси
непрерывна вместе со своими производными достаточно высокого порядка на всей оси  , кроме отдельных точек, в которых
, кроме отдельных точек, в которых  или ее производные терпят разрыв І-го рода, причем на каждом конечном интервале оси
или ее производные терпят разрыв І-го рода, причем на каждом конечном интервале оси 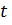 таких точек имеется лишь конечное число;
таких точек имеется лишь конечное число;
2) для всех отрицательных 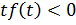
3) 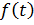 возрастает не быстрее показательной функции т.е. существуют такие постоянные
возрастает не быстрее показательной функции т.е. существуют такие постоянные 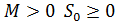 , что для всех
, что для всех 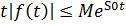 . Число
. Число 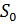 назовем показателем роста
назовем показателем роста  для ограниченных оригиналов можно, очевидно, принять
для ограниченных оригиналов можно, очевидно, принять 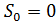 .
.
Простейшей функцией-оригиналом является так называемая единичная функция или функция Хевисайда:
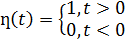
Очевидно, умножение функции 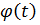 на
на 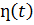 «гасит» эту функцию для
«гасит» эту функцию для 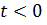 и оставляет без изменения для
и оставляет без изменения для  ; если функция
; если функция 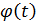 удовлетворяет условиям 1 и 3 и не удовлетворяет условию 2, то произведение:
удовлетворяет условиям 1 и 3 и не удовлетворяет условию 2, то произведение:

будет удовлетворять и условию 2, т.е. будет оригиналом (например,  и т.д.). Для простоты записи будем, как правило, опускать множитель
и т.д.). Для простоты записи будем, как правило, опускать множитель 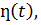 условившись, что все функции, которые будем рассматривать, равны нулю для всех отрицательных t. Например, вместо ƞ(t) будем писать 1, вместо
условившись, что все функции, которые будем рассматривать, равны нулю для всех отрицательных t. Например, вместо ƞ(t) будем писать 1, вместо 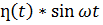 – просто
– просто  и т.д. Используя функцию Хевисайда:
и т.д. Используя функцию Хевисайда: 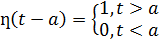 можно, функцию, заданную несколькими аналитическими выражениями, записать одни выражением. Например, если:
можно, функцию, заданную несколькими аналитическими выражениями, записать одни выражением. Например, если:
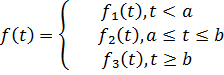 , то имеем:
, то имеем:
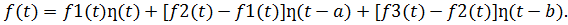
Изображением функции  (по Лапласу) называют функцию комплексного переменного
(по Лапласу) называют функцию комплексного переменного 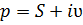 , определяемую соотношением
, определяемую соотношением

где интеграл берется по положительной полуоси. Фразу: «функция  имеет своим изображением
имеет своим изображением  » будет записываться так:
» будет записываться так: 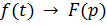 или
или 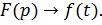
Теорема аналитичности.
Для всякого оригинала  изображение
изображение  определено в полуплоскости
определено в полуплоскости  где
где 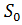 – показатель роста
– показатель роста  и является в этой полуплоскости аналитической функцией. Если точка
и является в этой полуплоскости аналитической функцией. Если точка  стремится к бесконечности так, что
стремится к бесконечности так, что 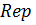 неограниченно возрастает, то
неограниченно возрастает, то  стремится к нулю:
стремится к нулю: 
Предельные соотношения.
Если  является оригиналом вместе со своей производной
является оригиналом вместе со своей производной 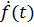 и
и  то
то 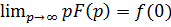 , где
, где  внутри угла
внутри угла 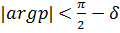 и
и  , если, кроме этого, существует
, если, кроме этого, существует 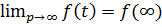 , то лимит
, то лимит 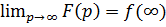 .
.
Теорема линейности.
Для любых действительных или комплексных постоянных 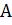 и
и 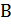
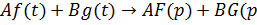 ), т.е. линейной комбинации оригиналов соответствует линейная комбинация изображений.
), т.е. линейной комбинации оригиналов соответствует линейная комбинация изображений.
Теорема подобия.
Для любого постоянного  , т.е. умножения аргумента оригинала на положительное число
, т.е. умножения аргумента оригинала на положительное число  приводит к делению аргумента изображения и самого изображения
приводит к делению аргумента изображения и самого изображения  на то же число
на то же число  .
.
Теорема затухания.
Для любого действительного или комплексного числа  , т.е. умножение оригинала на функцию
, т.е. умножение оригинала на функцию 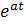 влечет за собой «смещение» независимой переменной
влечет за собой «смещение» независимой переменной  . Поэтому теорему называют также теоремой смещения.
. Поэтому теорему называют также теоремой смещения.
Теорема запаздывания.
Для любого постоянного 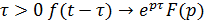 , т.е. запаздывание оригинала на время τ соответствует умножению изображения на
, т.е. запаздывание оригинала на время τ соответствует умножению изображения на 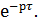
Теорема о дифференцировании по паракетру.
Если при любом  оригиналу
оригиналу  соответствует изображение
соответствует изображение 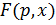 , то
, то 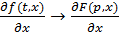 .
.
Теорема дифференцирования оригинала.
Если  , то
, то  т.е. дифференцирование оригинала сводится и умножению на
т.е. дифференцирование оригинала сводится и умножению на 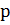 его изображения и вычитанию
его изображения и вычитанию 
Для повторного дифференцирования имеем:
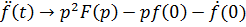
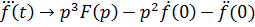

где под 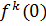 понимается правое предельное значение
понимается правое предельное значение 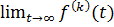 .
.
Теорема дифференцирования изображений.
Если  , то –
, то – 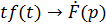 , т.е. дифференцирование изображения сводится к умножению оригинала на
, т.е. дифференцирование изображения сводится к умножению оригинала на  . Вообще,
. Вообще, 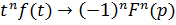 , где
, где 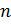 – натуральное число.
– натуральное число.
Теорема интегрирования оригинала.
Если  , то
, то 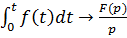 , т.е. интегрирование оригинала в пределах от
, т.е. интегрирование оригинала в пределах от 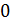 до
до  приводит к делению изображения на
приводит к делению изображения на 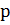 .
.
Теорема интегрирования изображения.
Если 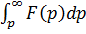 сходится, то
сходится, то  , т.е. интегрирование изображения от p до ∞ соответствует делению оригинала на
, т.е. интегрирование изображения от p до ∞ соответствует делению оригинала на  .
.
Теорема умножения изображения.
Если  и
и 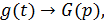 то выражению
то выражению  , называемому светркой функий
, называемому светркой функий  и
и  соответствует произведение изображений, т.е.
соответствует произведение изображений, т.е. 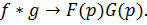
Существенное значение имеет так называемая формула Дюамеля:

Теорема умножения оригиналов.
Если  и
и 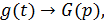 то
то 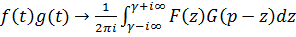 , т.е. произведение оригиналов соответствует свертка изображений. Функции
, т.е. произведение оригиналов соответствует свертка изображений. Функции  и
и 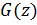 аналитичны при
аналитичны при  Функция
Функция 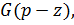 при условии
при условии 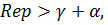 аналитична в полуплоскости
аналитична в полуплоскости 
При нахождении изображений по оригиналам и оригиналов по изображениям удобно пользоваться формулами соответствия, которые приведены в следующей таблице.
Таблица
| Номер формулы | Оригинал | Изображение |
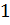 |  | |
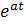 |  | |
 | 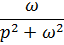 | |
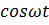 | 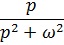 | |
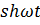 |  | |
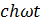 |  | |
 | 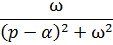 | |
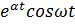 |  | |
 | 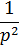 | |
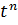 |  | |
 |  |
1.2 Нахождение изображения по оригиналу
Задачу о нахождении изображения по оригиналу можно решать, используя вышеприведенную таблицу и свойства преобразования Лапласа.
Пример 1. 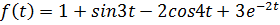 . Найти
. Найти  , используя теорему линейности и формулы соответствия, получим
, используя теорему линейности и формулы соответствия, получим

Пример 2.  . Найти
. Найти  .
.
 . Используя теорему линейности, теорему затухания и формулы соответствия, получим:
. Используя теорему линейности, теорему затухания и формулы соответствия, получим:
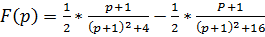 .
.
Пример 3.  . Найти
. Найти 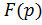 .
.
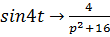 . Используя теорему об интегрировании изображения, находим:
. Используя теорему об интегрировании изображения, находим:
 .
.
Пример 4.  . Найти
. Найти  .
.
 . Используя теорему о дифференцировании изображения, находим
. Используя теорему о дифференцировании изображения, находим 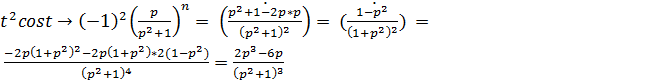 .
.
Пример 5. 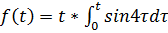 . Найти
. Найти 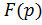
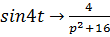 . Используя теорему об интегрировании оригинала, имеем
. Используя теорему об интегрировании оригинала, имеем  .
.
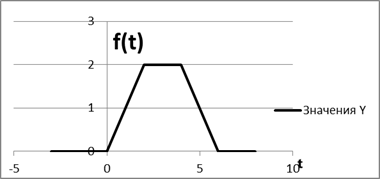
Пример 6. Найти F(p), если оригинал f(t) задан графиком

В аналитической форме 
Заметим, что на интервале (3,5) уравнение прямой найдено по формуле:
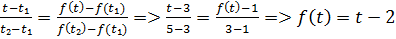 .
.
Применяя преобразования Лапласа, находим:
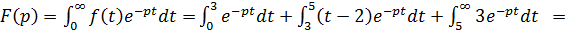
=  .
.
Другой способ решения этой задачи состоит в следующем. Используя функцию Хевисайда, имеем  .
.
Применяя теорему запаздывания и используя формулы соответствия, получим 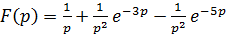 .
.
1.3 Нахождение оригинала по изображению.
В общем случае нахождение оригинала по изображению достигается использованием теоремы обращения.
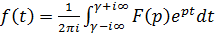 . (1.1).
. (1.1).
Однако для произвольных  это приводит к большим трудностям. Мы рассмотрим несколько удобных приемов нахождения
это приводит к большим трудностям. Мы рассмотрим несколько удобных приемов нахождения  в предположении, что
в предположении, что  – правильная рациональная функция, т.е. что
– правильная рациональная функция, т.е. что  – отношение двух многочленов, причем степень многочлена знаменателя выше степени многочлена числителя (заметим, что в формулах соответствия все
– отношение двух многочленов, причем степень многочлена знаменателя выше степени многочлена числителя (заметим, что в формулах соответствия все  рациональны). Разложим
рациональны). Разложим  на простейшие дроби. Получим:
на простейшие дроби. Получим:
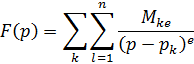
где 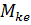 – комплексные числа,
– комплексные числа,  – нули знаменателя
– нули знаменателя 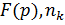 – их кратность. Пользуясь таблицей, легко получить:
– их кратность. Пользуясь таблицей, легко получить:
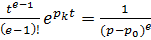 ,
, 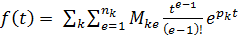 .
.
Часто бывает удобнее разложить изображение на простейшие дроби вида:
 ,
,  ,
, 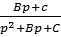
При этом также можно использовать формулы соответствия.
Пример 1. 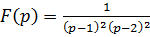 . Найти
. Найти  .
.
Разложим дробь 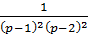 на простейшие дроби:
на простейшие дроби:

Полагая:  , имеем
, имеем 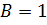
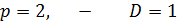
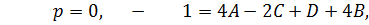

Используя теорему линейности и формулы соответствия, получим:
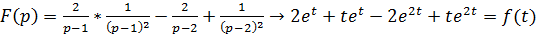 .
.
При нахождении f(t) по F(p) иногда целесообразно использовать теорему о произведении изображений (теорему о свертке).
Пример 2. 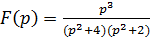 . Найти
. Найти  .
.
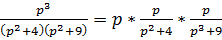 ;
;  ,
, 
По формуле Дюамеля имеем:
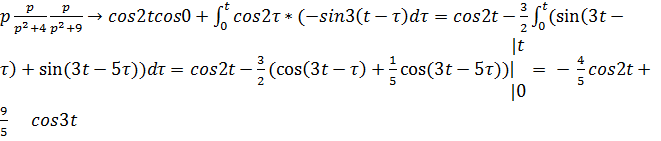 .
.
Можно находить  по
по 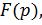 используя теорию вычетов (теорему разложения, которая выводится из (1.1)), а именно, если
используя теорию вычетов (теорему разложения, которая выводится из (1.1)), а именно, если  – правильная рациональная дробь, то
– правильная рациональная дробь, то  ,где
,где 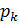 – полюсы функции
– полюсы функции  .
.
Пример 3. 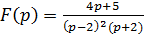 . Найти оригинал.
. Найти оригинал.
Функция F(p) имеет два полюса 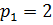 – второй кратности и
– второй кратности и 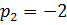 – простой полюс. По теореме разложения находим:
– простой полюс. По теореме разложения находим:
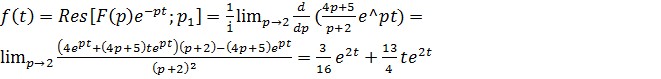 .
.
 .
.
 .
.
Рассмотрим применение теоремы запаздывания при нахождении оригинала по данному изображению на следующем примере.
Пример 4. 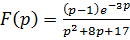 . Найти
. Найти 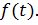
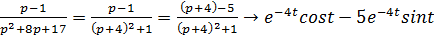
Учитывая, что 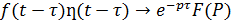 , если
, если  , получи:
, получи:
 ,
,

Если все полюсы  простые, то формула
простые, то формула 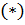 принимает вид:
принимает вид:
 , где сумма берется по всем корням
, где сумма берется по всем корням 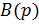 .
.
В приложения, главным образом электротехнических, важнее разновидность предыдущей формулы, когда 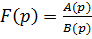 , где степень
, где степень 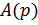 не превосходит степени
не превосходит степени 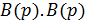 имеет простые корни, отличные от нуля. Тогда:
имеет простые корни, отличные от нуля. Тогда: 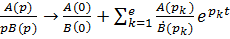 .
.
1.4 Решение линейных дифференциальных уравнений операционным методом.
Операционный метод особенно просто применяется к решению линейных дифференциальных уравнений с постоянными коэффициентами и систем таких уравнений. Одно из достоинств этого метода состоит в том, что он не связан с нахождением линейно-независимых решений линейного однородного уравнения, что необходим в методе неопределенных коэффициентов при нахождении общего решения неоднородного уравнения.
Операционный метод особенно удобен при расчете сложных электрических цепей при произвольном внешнем напряжении.
Пусть дано линейное дифференциальное уравнение:
 ,
, 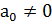 ,
,  – постоянные коэффициенты, а начальные условия
– постоянные коэффициенты, а начальные условия 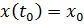 ,
, 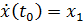 . Требуется найти решение
. Требуется найти решение 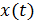 данного уравнения, удовлетворяющее начальным условиям. Будем считать, что
данного уравнения, удовлетворяющее начальным условиям. Будем считать, что  и решение
и решение 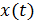 , а также
, а также 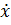 и
и 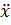 – оригиналы. Пусть
– оригиналы. Пусть
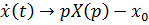 ,
,  .
.
Применим к обеим частям уравнения преобразования Лапласа, получим алгебраическое уравнение:

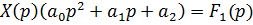 ,
, 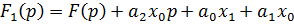
Отсюда 
Переходя от этого изображения к его оригиналу, получим искомую функцию 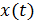 .
.
Пример 1. 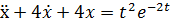 ,
, 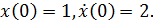
 ,
,  ,
,
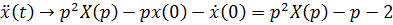 ;
;
 ;
;
 ;
;
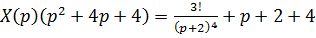 ;
;
 .
.
Используя формулы соответствия и теорему линейности, имеем:
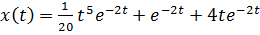
Отметим особую роль формулы Дюамеля при решении линейных дифференциальных уравнений с постоянными коэффициентами. Пусть требуется решить линейное дифференциальное уравнение с постоянными коэффициентами 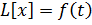 при нулевых начальных условиях. Если известно решение
при нулевых начальных условиях. Если известно решение 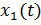 уравнения
уравнения 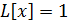 с той же левой частью, а правой частью, равной 1, также при нулевых начальных условиях, то формулы Дюамеля позволяет написать решение данного уравнения без всяких вычислений. В самом деле, операторные уравнения, соответствующие данному уравнению и с правой часть 1, имеют вид
с той же левой частью, а правой частью, равной 1, также при нулевых начальных условиях, то формулы Дюамеля позволяет написать решение данного уравнения без всяких вычислений. В самом деле, операторные уравнения, соответствующие данному уравнению и с правой часть 1, имеют вид  ,
,  , где
, где  – изображение
– изображение  , откуда
, откуда 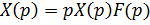 . Тогда, согласно формуле Дюамеля,
. Тогда, согласно формуле Дюамеля, 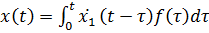 или
или 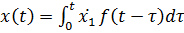 , или
, или  .
.
Пример 2. Решить дифференциальное уравнение с нулевыми начальными условиями, т.е.  .
.
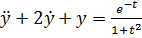 .
.
Решаем сначала уравнение  операционным методом:
операционным методом:
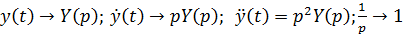 ;
;
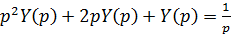 ;
;
Разложим 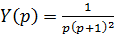 на простейшие дроби:
на простейшие дроби:
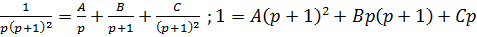

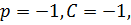
Получим 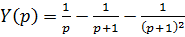 . Используя теорему линейности и формулы соответствия, получим
. Используя теорему линейности и формулы соответствия, получим  ,
, 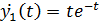 . Применяя формулу Дюамеля, имеем:
. Применяя формулу Дюамеля, имеем:
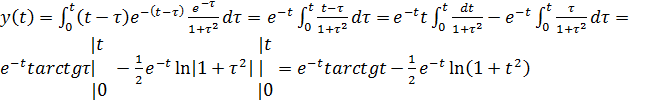 .
.
1.5 Решение систем линейных уравнений операционным методом.
Дана система двух линейных дифференциальных уравнений

и начальные условия 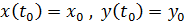 . Требуется найти частное решение
. Требуется найти частное решение 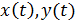 данной системы, удовлетворяющие данным начальным условиям. Будем считать, что
данной системы, удовлетворяющие данным начальным условиям. Будем считать, что
 .
.
На основании теоремы о дифференцировании оригиналов находим:
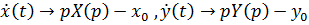
Применяя к дифференциальным уравнениям преобразования Лапласа, получаем систему алгебраических уравнений:

Решая эту систему, найдем  , а затем и их оригиналы
, а затем и их оригиналы 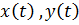 – искомые функции.
– искомые функции.
Пример 1. Решить систему

Пусть 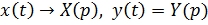 , тогда:
, тогда:

Система операторных уравнений имеет вид:
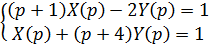
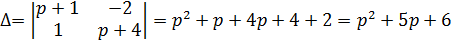



Используя теорему линейности и таблицу соответствия, получаем:
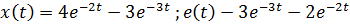
Примеры решения творческих задач
Пример 1. Найти общее решение уравнения
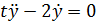 (2.1)
(2.1)
Решение. Пусть 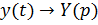 . Тогда:
. Тогда:
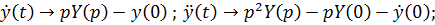

Уравнение (2.1) Принимает вид:
 Интегрируем это линейное уравнение 1-го порядка относительно
Интегрируем это линейное уравнение 1-го порядка относительно 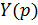 , найдем
, найдем 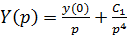 , откуда
, откуда 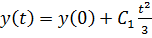 – решение.
– решение.
Пример 2. Решить операционным методом уравнение:
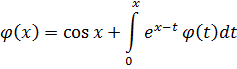
Решение. При переходе от оригинала к изображению 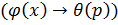 рассматриваем интеграл как свертку и, применяя теорему о свертке, получи:
рассматриваем интеграл как свертку и, применяя теорему о свертке, получи:
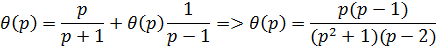
Переходя от изображения к оригиналу, получим:
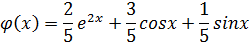
Минимум задач
Задание 1. По данному оригиналу найти изображение
1. 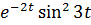
2. 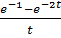
3. 
4. 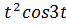
5. 
6. 
7. 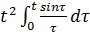
8. 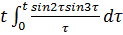
9. 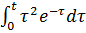
Задание 2. Найти изображение функции  , заданной графически.
, заданной графически.
1)

2)

3)

4)
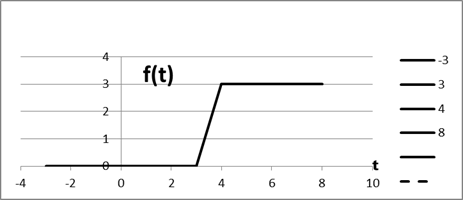
Задание 3. По данному изображению найти оригинал.
1)  9)
9) 
2) 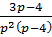 10)
10) 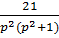
3)  11)
11) 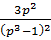
4)  12)
12) 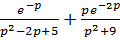
5) 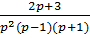 13)
13) 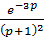
6) 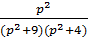 14)
14) 
7)  15)
15) 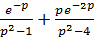
8) 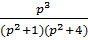
Задание 4. Решить дифференциальное уравнения при заданных начальных условиях.
1) 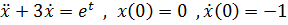
2) 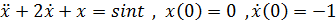
3) 
4) 
5) 
Задание 5. С помощью формулы Дюамеля найти решение уравнений, удовлетворяющих заданным начальным условиям.
1) 
2) 
3) 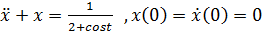
4) 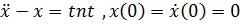
5) 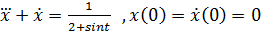
Задание 6. Решить систему уравнений.
1) 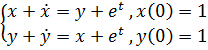
2) 
3) 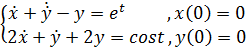
4) 
Ответы к минимуму задач.
Задание 1.
1) 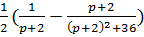
2) 
3) 
4) 
5) 
6) 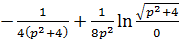
7) 
8) 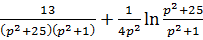
9) 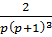
Задание 2.
1) 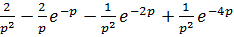
2) 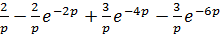
3) 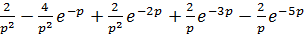
4) 
Задание 3.
1) 
2) 
3) 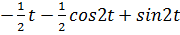
4) 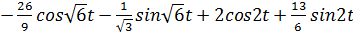
5) 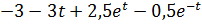
6) 
7) 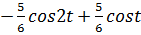
8) 
9) 
10) 
11) 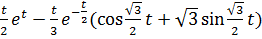
12) 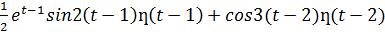
13) 
14) 
15) 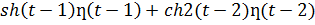
Задание 4.
1) 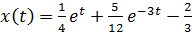
2) 
3) 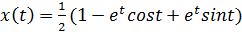
4) 
5) 
Задание 5.
1) 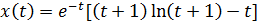
2) 
3) 
4) 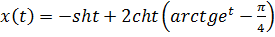
5) 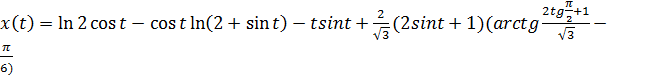
Задание 6.
1) 
2) 
3) 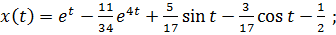

4) 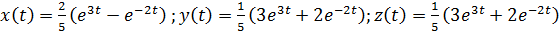
Варианты контрольных работ.
Работа №1.
1)  Найти
Найти 
2) Функция  задана графиком. Найти
задана графиком. Найти 
 Найти
Найти 
 Найти
Найти 
Работа №2.
1) Решить уравнения:
¾ 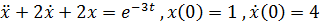
¾ 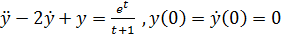
2) Решить систему уравнений: