ЛЕКЦИЯ 19. Двумерное преобразование Фурье
Пусть f(x1, x2) – функция двух переменных. По аналогии с одномерным преобразованием Фурье можно ввести двумерное преобразование Фурье:
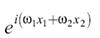
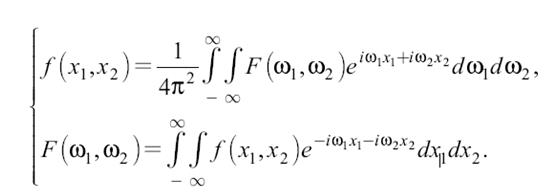
Функция при фиксированных значениях ω1, ω2 описывает плоскую волну в плоскости x1, x2 (рисунок 19.1).
Величины ω1, ω2 имеют смысл пространственных частот и размерность мм−1, а функция F(ω1, ω2) определяет спектр пространственных частот. Сферическая линза способна вычислять спектр оптического сигнала (рисунок 19.2). На рисунке 19.2 введены обозначения: φ — фокусное расстояние,
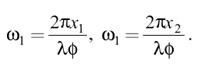
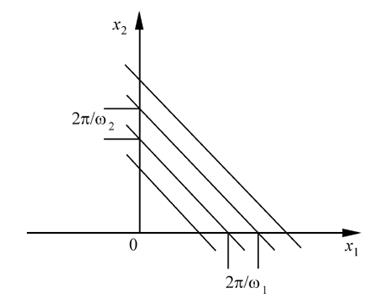
Рисунок 19.1 – К определению пространственных частот
Двумерное преобразование Фурье обладает всеми свойствами одномерного преобразования, кроме того отметим два дополнительных свойства, доказательство которых легко следует из определения двумерного преобразования Фурье.
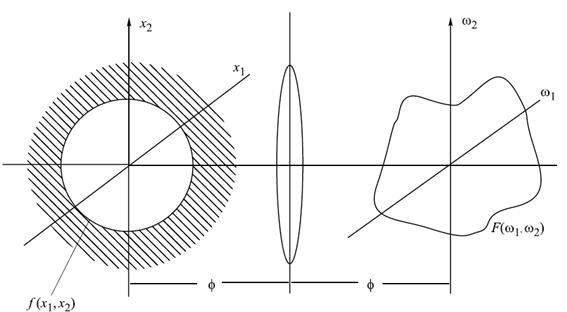
Рисунок 19.2 – Вычисление спектра оптического сигнала с использованием
сферической линзы
Факторизация. Если двумерный сигнал факторизуется,
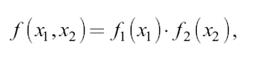
то факторизуется и его спектр:
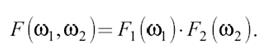
Радиальная симметрия. Если двумерный сигнал радиально-симметричен, то есть
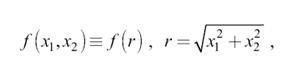
то
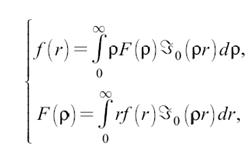
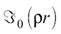 где – функция Бесселя нулевого порядка. Формулу, определяющую связь между радиально-симметричным двумерным сигналом и его пространственным спектром называют преобразованием Ганкеля.
где – функция Бесселя нулевого порядка. Формулу, определяющую связь между радиально-симметричным двумерным сигналом и его пространственным спектром называют преобразованием Ганкеля.
ЛЕКЦИЯ 20. Дискретное преобразование Фурье. Низкочастотный фильтр
Прямое двумерное дискретное преобразование Фурье (ДПФ) преобразует изображение, заданное в пространственной координатной системе (x, y), в двумерное дискретное преобразование изображения, заданное в частотной координатной системе (u,v):
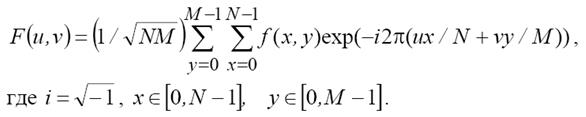
Обратное дискретное преобразование Фурье (ОДПФ) имеет вид:
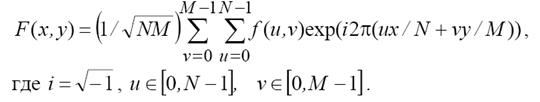
Видно, что ДПФ является комплексным преобразованием. Модуль этого преобразования представляет амплитуду спектра изображения и вычисляется как корень квадратный из суммы квадратов действительной и мнимой частей ДПФ. Фаза (угол сдвига фазы) определяется как арктангенс отношения мнимой части ДПФ к действительной. Энергетический спектр равен квадрату амплитуды спектра, или сумме квадратов мнимой и действительной частей спектра.
Теорема о свертке
В соответствии с теоремой о свертке, свертка двух функций в пространственной области может быть получена ОДПФ произведения их ДПФ, то есть
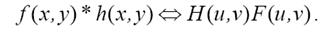
Фильтрация в частотной области позволяет по ДПФ изображения подобрать частотную характеристику фильтра, обеспечивающую необходимое преобразование изображения. Рассмотрим частотные характеристики наиболее распространенных фильтров.
