Измерение и построение углов с помощью транспортира

Навыки измерения и построения углов с помощью транспортира вырабатываются у учащихся медленно, требуется большое коли­чество упражнений, кропотливая индивидуальная работа с каждым учеником.

Можно отметить характерные ошибки, встречающиеся у умст­венно отсталых детей при измерении углов транспортиром. Дети совмещают вершину угла не с центром транспортира, а с точкой пересечения дуги с линейкой. Не понимают, какое деление пока­зывает величину угла (по какой дуге ведется отсчет). Большие трудности возникают у учащихся, когда величина измеряемого угла выражена не круглым числом. Совместив вершину угла с цент­ром транспортира, некоторые ученики не совмещают линейку транс­портира с одной из сторон угла. Часто дети передвигают не транспор­тир, а чертеж, если одна из сторон угла не параллельна нижнему краю тетради.

При построении углов с помощью транспортира учащиеся до­пускают чаще всего одну основную ошибку: строят угол не заданный, а смежный с ним. Например, нужно построить угол 30°, а они строят угол не заданный, т. е. 30°, а угол, смежный с ним, т. е. 150°. Причем в силу некритичности мышления, неумения контролировать свою деятельность их не смущает, что получился не острый, а тупой угол.

Наблюдения и опыт показывают, что для учащихся вспомога­тельной школы легче произвести построение углов с помощью транс­портира, чем их измерение. Сначала надо научить вычерчивать

угол данного размера, отмечая три точки: центр транспортира, нулевой штрих на пересечении дуги и линейки транспортира и штрих на дуге, соответствующей величине угла. Последний штрих дети находят считая от нуля круглыми десятками, одновременно указывая карандашом на штрихи дуги 10°, 20°, 30° и т. д. до заданного числа. При этом, как показывает опыт, количество ошибок при нахождении градусной меры угла на шкале транспортира значи­тельно сокращается. Получив (отметив) три точки, ученики их соединяют (точку — вершину угла с двумя другими).

Затем школьники учатся располагать транспортир на листе бу­маги таким образом, чтобы его центр совпадал с заданной точкой.

При другом варианте построения вычерчивается произвольная прямая, которая должна содержать сторону угла. Дети совмещают линейку транспортира с этой прямой, отмечают на прямой точку — вершину будущего угла, а затем от нулевого штриха отсчитывают заданное количество градусов (10°, 20°, ... и т. д.). Нужное количество градусов отмечают точкой на плоскости.

Убрав транспортир, они соединяют эту точку вне прямой с точкой-вершиной. Если школьники забудут, по какой дуге транспор­тира они производили отсчет, то может быть неправильно выделена внутренняя область угла: вместо острого угла они получают тупой угол или наоборот. Поэтому важно, чтобы до вычерчивания угла они называли вид угла, т. е. какой угол должен быть начерчен: прямой, острый или тупой.

Для предупреждения такого рода ошибок полезно предложить учащимся определить в градусах размеры прямых, острых и тупых углов (прямые углы — 90°, острые углы содержат от 0° до 90°, ту­пые — от 90° до 180°, развернутый угол— 180°). Построить углы (и произвольном положении) заданной градусной меры: 15°, 90°, 30°, 80⁰, 120°, 175°, 90°, расположив углы на странице тетради под соответствующими рубриками: «Острые углы», «Тупые углы», «Пря­мые углы». Для выполнения этого упражнения необходимо разде­лить, страницу на 3 равные части, сделать заголовки. Прежде чем вычертить угол, учащиеся должны обдумать, какой угол должен получиться и где его следует расположить.

Последний случай построения угла с помощью транспортира — когда задана прямая (сторона будущего угла) и точка на прямой — вершина угла.

При измерении угла с помощью транспортира учитель учит детей правильно совмещать транспортир с элементами угла: центр транспортира должен совпадать с вершиной данного угла, линейка транспортира — располагаться по одной из сторон угла, вторая сто­рона угла — пересекать дугу транспортира. Точка пересечения дуги транспортира со стороной угла показывает градусную меру этого угла.

Для выработки навыков построения и измерения углов требуется достаточное количество упражнений. Учащиеся работают с большим интересом, если учитель организует взаимопроверку работ. Так, сначала дети строят углы по заданным размерам или про-

извольных размеров, устанавлива­ют их градусную меру и указыва­ют ее на чертеже угла. После это­го они обмениваются работами и осуществляют взаимный конт­роль.

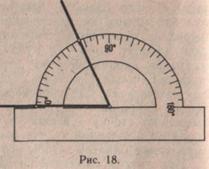
Особенно важно научить изме­рять углы в различном их положе­нии. Учащиеся вспомогательной школы, как правило, при измере­нии угла в непривычном для них положении стараются повернуть чертеж так, чтобы угол снова при­нял привычное положение, т. е. изменяют положение чертежа, а не транспортира. И здесь важно, чтобы дети усвоили, что при из­мерении углов нужно менять положение транспортира, а не черте­жа (рис. 18.).

Не менее важно научить учащихся правильно отсчитывать деле­ния по дуге от нулевого штриха до точки пересечения дуги со второй стороной угла.

Полезно раздать учащимся карточки с изображениями углов в разных положениях. Дети измеряют углы, записывают их градусную меру, затем обмениваются карточками для взаимного контроля.

Готовя учащихся к построению треугольника по стороне и двум прилежащим углам (VII класс), необходимо научить их строить угол с различным положением (на плоскости) его области по отно­шению к вершине. Можно пользоваться выражениями: «Угол на­ходится справа от вершины. Угол находится слева от вершины». В этих случаях дети при построении угла нулевую точку отмечают справа от центра транспортира (т. е. от вершины угла) или слева.

Далее учащиеся упражняются в использовании транспортира при изучении многоугольников и при их построении (треугольники, четырехугольники).

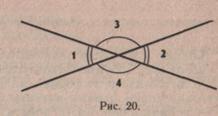
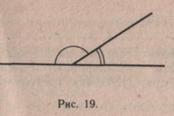
В VII классе школьники знакомятся со смежными углами, изу­чают их свойства, определяют,- сколько градусов содержит угол, если известен другой, смежный с ним (рис. 19).

При ознакомлении со смежными углами целесообразно опираться на большую самостоятельность учащихся. Наш опыт показывает, что учащимся, успевающим по математике, под силу при самостоя­тельном рассмотрении двух смежных углов определить их свойства. Слабые учащиеся также могут дать описание смежных углов, но только с помощью наводящих вопросов учителя: «Что изображено на чертеже? Сколько углов здесь вы видите? Покажите стороны первого угла. Покажите стороны второго угла. Какая сторона у них общая? Что вы можете сказать о двух других сторонах углов? Какие углы называются смежными?»

Далее учащимся предлагается составить смежные углы с по­мощью палочек (планок) и пластилина. Затем начертить их в тет­радях, измерить каждый угол с помощью транспортира и найти их

сумму. Так как каждый измерял свои, им начерченные углы, а сумма получилась одинаковая — 180°, то дети сами смогут сделать вывод о свойстве смежных углов.

Учитель обращает внимание школьников на то, что смежные углы составляют развернутый угол, а развернутый угол равен 180°.

Когда представление о смежных углах будет сформировано, вычисление угла, смежного с данным, превращается в вычислитель­ную задачу и может включаться в устный счет на всех уроках математики.

Смежные углы могут быть рассмотрены также и на примере углов, образующихся при пересечении двух прямых (рис. 20). Ра­венство углов между собой может быть доказано с помощью опре­деления смежных углов.

1) l + 3=180°
2 + 3=180°
3= 3, значит, 1 = 2

2) 3 + 2=180°
4 + 2=180°
2 = 2, значит, 3 = 4

Таким образом, при пересечении двух прямых достаточно изме­рить один угол, остальные углы можно вычислить, пользуясь свойст­вом смежных углов.

Например, при пересечении двух прямых оказалось, что один из острых углов равен 70°, необходимо вычислить величину осталь­ных углов.

1 + 3=180°

3=180°— 1

.3= 4= 180° — 70° = 110°

Возможно и другое решение поставленной задачи:

1 = 2 = 70°

1 + 2 = 70° + 70° = 140°

3+ 4 = 360°—I40° = 220°

3= 4 = 220°: 2 = 110°

Такое подробное изучение углов, образующихся при пересечении двух прямых, оправдано. В будущем это поможет учащимся более полно усвоить особенности диагоналей изучаемых четырехуголь­ников.

МНОГОУГОЛЬНИКИ

Впервые школьники знакомятся с многоугольниками в I классе. Из всего многообразия многоугольников рассматриваются только три, отличающиеся по форме: квадрат, прямоугольник, треугольник. Первоклассники должны научиться:

1) отбирать фигуры по образцу;

2) узнавать и называть фигуры, когда им предъявляются модели, чертежи фигур;

3) отбирать по названию из множества разнообразных фигур только квадраты, только прямоугольники или только треугольники;

4) узнавать в предметах, имеющих форму многоугольника, знако­мые им геометрические фигуры.

Учитывая косность, тугоподвижность мышления учащихся, огра­ниченный запас их представлений, для успешного изучения фигур учителю необходимо иметь большое количество моделей фигур раз­ных размеров, изготовленных из различного материала, окрашенных в разные цвета: прямоугольники, треугольники с разной длиной сторон и треугольники с разной величиной углов. Эти модели используются и в качестве раздаточного материала для организации самостоятельной работы. Для демонстрации используются не только модели фигур, но и таблицы с изображением чертежей квадратов, любых прямоугольников, треугольников.

Опыт показывает, что целесообразно изучать фигуры в такой последовательности: квадрат, треугольник, любой прямоугольник.

Квадрат

Квадрат знаком учащимся I класса вспомогательной школы из дидактических игр, но они склонны называть его «квадратик», «окошко».

На урок, который отводится формированию первых представле­ний о квадрате, учитель приносит модели этой фигуры, показы­вает и называет их. Из множества фигур он предлагает учащимся выбрать по образцу только квадраты и назвать их. Квадраты раздаются учащимся. Они обводят их контуры на листе бумаги, в тетради, раскрашивают в различные цвета, заштриховывают, пересчитывают. Среди игрушек и других вещей дети отыскивают предметы, которые имеют форму квадратов.

Важно задавать учащимся такие вопросы, в ответах на которые они употребляли бы слово квадрат. Например: «На какую фигуру похожа салфетка, носовой платок? Какой фигурой является клеточка тетради?» И т. д.

Аналогично учащиеся знакомятся с прямоугольником любого вида и с треугольником.

Следует обратить внимание на то, что в I классе, пока учащиеся еще не знакомы со свойствами фигур, прямоугольник по форме

должен значительно отличаться от квадрата, т. е. разница между его длиной и шириной должна быть значительной.

После того как дети смогут узнавать и называть квадраты, любые прямоугольники, треугольники, следует научить их выделять перечисленные фигуры из множества других еще им незнакомых многоугольников.

При изучении геометрических фигур в младших классах необходи­мо больше развивать зрительное восприятие, для этого нужно предъявлять фигуры разного цвета, размера при определенной фор­ме. Учащиеся развивают тактильное восприятие, когда пальчиком обводят по контуру фигуру, гладят ее ладошкой, определяя форму на ощупь; слуховое восприятие, когда название фигуры не только учащиеся слышат, но и произносят сами, т. е. оно включается в активный их словарь.

Предметно-практическая и игровая деятельность являются веду­щими при изучении геометрических фигур: отбор фигур, обводка, лепка, раскрашивание, штриховка, конструирование из геометриче­ских фигур различных предметов (елочка, домик, паровозик, тележ-ка и т. д.), игры («Чудесный мешочек», «Найди такую же фигуру», «Что изменилось?», «Какой фигуры не стало?», «Куда пойдешь, что найдешь?» и др.).

Уже в I классе можно познакомить учащихся со сравнением фигур приемом наложения. Фигуры для этого надо брать или одинаковые, или настолько различные по размерам, что одна фигура сможет целиком уместиться на другой.

Важно проводить упражнения на дифференциацию знакомых ученикам фигур: квадрата, треугольника, любого прямоугольника. Целесообразнее всего это делать в дидактических играх, в зри­тельных и слуховых диктантах.

Большое внимание следует уделить обучению детей ориентировке мл плоскости. Например, учитель предлагает учащимся положить перед собой красный квадрат, а около него расположить другой квадрат, третий квадрат поместить над ним, четвертый — под ним, пятый — слева или справа от него и т. д. (рис. 21).

Инструкции учителя о расположении фигур на плоскости должны быть немногословными. Характеризуя положение фигур, он может пользоваться только такими выражениями, которые доступны для понимания и повторения учащимися. Так, учитель, показывая, как нужно положить, например, квадрат и треугольник, говорит: Треугольник лежит справа, квадрат лежит слева. Повторите, где лежит треугольник, где лежит квадрат». Или: «Треугольник лежит справа от квадрата. Повторите. Квадрат лежит слева от треуголь­ника. Повторите...» И т. п.

Чтобы подготовить детей к выделению фигур на окружающих реальных предметах, можно сначала предложить им рисунки этих предметов, на которых контуром выделить (обвести) знакомую уча­щимся фигуру. Например, изображен почтовый конверт. Его контур (прямоугольник) выделен жирной линией. Дан рисунок с изображе­нием Буратино, его колпачок, имеющий форму треугольника, также

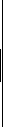выделен ярким контуром. Учи­тель подбирает к урокам реаль­ные предметы, имеющие форму квадрата, любого прямоугольника, треугольника, изготавливает точ­но по их контуру модели фигур. Рассмотрев модели, назвав фигу­ры, учащиеся или учитель совме­щают модель фигуры и поверх­ность предмета (коробки, пенала, тетради, книги, кубика и пр.).

Учащиеся узнают в предметах и

называют знакомую фигуру. В ходе работы над многоугольниками на всех годах обучения учитель должен широко пользоваться приемом сравнения, исполь­зовать классификацию. Так, предложив рассмотреть модели прямо­угольников, квадратов, треугольников, учитель просит учащихся подобрать такие же фигуры другого цвета, размера. Можно пред­ложить задание, когда множество фигур, в которое входят треуголь­ники, квадраты, круги, требуется разложить на три группы, и т. п. Во II классе дети продолжают работу над многоугольниками: они учатся выделять элементы этих фигур, вычерчивают их.

Изучение каждой фигуры проходит последовательно. Например, учащиеся знакомятся с элементами квадрата. Учитель показывает на углы квадрата, просит пересчитать углы, показать их вершины и тоже пересчитать. С помощью чертежного треугольника дети определяют вид углов квадрата и приходят к выводу: «У квадрата углы прямые».

Далее учитель показывает стороны квадрата. Учащиеся пере­считывают их, меркой измеряют длины сторон и убеждаются, что стороны равны. На листах бумаги или в тетрадях учитель ставит точки (намечает вершины квадрата), просит соединить их отрезками и определить, какая фигура получилась, затем закрасить или заштри­ховать. На первых порах при организации фронтальной работы с классом вычерчивание фигур по точкам можно организовать поэтап­но. Например: «Соединим две верхние точки — это одна сторона, соединим две нижние точки — это вторая сторона, теперь соединим концы отрезков (сторон) справа, концы отрезков (сторон) слева, получим еще две стороны фигуры. Какая получилась фигура? Сколь­ко у нее сторон?» Каждый ученик должен проверить, все ли стороны полученной фигуры равны и все ли ее углы прямые. Только тогда он может утверждать, что построен квадрат. Затем к учащимся предъявляется больше требований в организации самостоятельной практической работы. Ученики учатся рассказывать, как они будут чертить квадрат или другую фигуру, и только после таких пояснений приступают к практической работе.

Можно изготовить модели фигур из деревянных планок или проволоки. Например, учитель говорит: «Будем из планок складывать

квадрат. Сколько надо взять планок? (Планки только одной длины.) Какие должны быть планки по длине? Почему? Сколько надо взять шариков пластилина (вершин), чтобы соединить планки (сто­роны)?»

В дальнейшем аналогично изучаются элементы треугольника и любого прямоугольника. Обязательно нужно сравнить прямоуголь­ник и треугольник, подчеркнув, что элементы каждой из фигур одни и те же — стороны и углы, но их количество различно.

Среди прямоугольников дети выделяют прямоугольники с рав­ными сторонами — квадраты. У квадрата все стороны равны, а у прямоугольника стороны равны попарно.

Определение вида фигур как на моделях, так и на окружающих предметах можно проводить с использованием мерок. Так, устанав­ливая, какую форму имеет форточка или другой реальный объект, учащиеся, получив от учителя бумажную ленту, укладывают ее вдоль одной из сторон, отрывают кусок ленты, а затем этой меркой измеряют остальные стороны. Если все стороны форточки равны, то форточка имеет форму квадрата, если попарно равны, то прямоуголь­ника. Дети устанавливают, что у треугольника стороны могут быть разные по длине, все три равные или только две.

Для учащихся должен стать очевидным тот факт, что количество сторон углов (вершин) в одном многоугольнике всегда одина­ково.

В связи с этим надо чаще ставить вопросы: «Фигура имеет четыре вершины. Сколько у нее углов, сторон?», «Фигура имеет 6 углов. Как называется такая фигура? Сколько у нее вершин, сторон?» Или: «Многоугольник называется пятиугольным. Ско­лько у него углов?» Таким образом у учащихся формируется умение мыслить обратимо.

Во II классе в начале года точки (вершины), по которым дети вычерчивают многоугольники, изображает учитель. Затем дети должны это делать сами. Вычерчивание производится на бумаге в клетку. Для построения квадрата необходимо сначала изобразить одну точку («вершину» одной из клеток), а затем по линейкам тетради отсчитать от нее равное количество клеток и изобразить две другие точки. Четвертая точка (вершина) находится на пересече­нии тех линеек тетради, которые проходят через две предыдущие точки (рис. 22).

Аналогично вычерчивается и любой прямоугольник, только от первоначально взятой точки отсчитывается разное количество клеток. Для построения треугольника сначала берутся две точки, соеди­няются отрезком; третья точка изображается вне этого отрезка.

Надо показать детям, что, если третья точка окажется на прямой, проходящей через первые две, треугольника не получится.

В III классе дети знакомятся
новым для них термином много-
гольник. _____________________________

Рассматриваются различные многоугольники, которым дается на­звание по количеству углов: треугольники, четырехугольники, пяти­угольники и т. д. (на моделях, таблицах). Всем вместе им дается общее название — многоугольники. Затем следует задание указать многоугольник по его названию или назвать его по данной модели, чертежу.

У каждого многоугольника устанавливается количество вершин, углов, сторон. На основании этих данных учащиеся должны дать название многоугольника. Можно ставить и обратную задачу: уча­щиеся не видят многоугольника, а учитель сообщает его название, например пятиугольник. Учащиеся должны назвать число его углов, вершин, сторон.

Произвольные многоугольники (четырехугольники, пятиугольни­ки и т. д.) строятся по точкам (вершинам). Точки отмечают сами учащиеся, помня, что три точки не должны лежать на одной прямой. Возможен и такой вариант, когда точки отметит учитель, а учащиеся, еще до построения многоугольника, должны дать его название, определить количество углов, сторон.

Большое место в программе вспомогательной школы уделяется изучению четырехугольников. Среди них есть уже знакомые уча­щимся фигуры: прямоугольники (квадраты).

В III классе на уроке, посвященном изучению темы «Прямо­угольник», ставится цель выделить из четырехугольников прямо­угольники, объяснить происхождение названия «прямоугольник», познакомить со свойствами прямоугольника.

В качестве наглядных пособий используются многоугольники различных видов (треугольники, четырехугольники, в том числе прямоугольники и в их числе — квадраты, пяти- и шестиугольники), круги. Аналогичные модели геометрических фигур, но меньших раз­меров, имеются и у учащихся.

Сначала все геометрические фигуры разделяются на две группы: многоугольники и круги (убираются круги). Затем многоугольники классифицируются по количеству углов (убираются все много­угольники, кроме четырехугольников). Наконец, происходит клас­сификация четырехугольников по видам углов. Выделяются четырех­угольники, у которых все четыре угла прямые, это прямоугольники(сюда же относятся и квадраты). В окружающей обстановке отыс­киваются предметы, имеющие форму прямоугольников.

«По каким признакам мы узнали прямоугольники?» — спраши­вает учитель. «Прямоугольник — это четырехугольник с прямыми углами»,— отвечают ученики. Учитель просит отметить в прямоуголь­нике прямые углы, указать их вершины, стороны. Далее каждый ученик измеряет стороны своего прямоугольника и приходит к выводу, что противолежащие (противоположные) стороны прямо­угольника равны.

Учитель просит учащихся доказать на модели прямоугольника, что противоположные стороны прямоугольника равны. Не все уча­щиеся могут решить эту задачу. Но она их заинтересовывает. Учитель показывает, что противоположные стороны совмещаются

при перегибании прямоугольника, или «берет на циркуль» одну из сторон и прикладывает циркуль к противоположной стороне.

Можно также построить отрезок, равный одной из сторон, и приложить его к противоположной стороне.

У некоторых учащихся может вызвать определенные трудности усвоение термина «противоположные» стороны. Поэтому целе­сообразно организовать ряд специальных упражнений по накоплению учащимися жизненного опыта. Например, учитель показывает про­тивоположную стену класса, встает в угол класса, а школьников просит указать противоположный угол. На прогулке или экскурсии учитель показывает противоположную сторону улицы. Учитель сооб­щает, что почта и магазин находятся на противоположных сторонах улицы. В школе они называют классы, расположенные друг против друга, т. е. на противоположных сторонах коридора, и т. д.

Когда учащиеся смогут правильно использовать в своей речи и действиях понятие «противоположные», можно перейти к рассмот­рению противоположных сторон любого прямоугольника.

Учитель показывает и называет элементы прямоугольника: ос­нования (верхнее и нижнее), боковые стороны (левая и правая), т. е. пары противоположных сторон.

Далее из прямоугольников выделяются квадраты:у учащихся но нескольку прямоугольников, среди которых есть и такие, у которых все стороны равны. Предлагается измерить стороны этих прямоугольников. Получается два вида прямоугольников: у одних равны только противоположные стороны, у других равны все стороны. Учитель говорит: «Прямоугольники- с равными сторонами называ­ются квадратами». Таким образом, квадрат рассматривается как частный случай прямоугольника.

В квадрате (по аналогии с прямоугольником) учащиеся на­ходят и называют основания, боковые стороны.

Уже в 1П классе следует показать, что противоположные сто­роны не имеют общих точек.

В V классе школьники знакомятся с диагоналями четырех­угольников. Предварительно при повторении уже известных уча­щимся элементов прямоугольника (квадрата), кроме противополож­ных сторон, следует выделить и противоположные вершины. Так как с V класса дети учатся обозначать точки большими буквами латинского алфавита, можно не только показывать, но и называть противоположные вершины и стороны.

Учитель просит всех учащихся соединить одним отрезком две противоположные вершины прямоугольника, т. е. провести диаго­наль. Другим отрезком — две другие противоположные вершины. «Как называется этот отрезок? Сколько диагоналей мы провели в прямоугольнике? Можно ли еще провести диагонали в прямоуголь­нике? Какие точки соединяют диагонали? Какие вершины соединяют диагонали?» — спрашивает учитель. Затем дается определение диагонали: «Диагональ прямоугольника (квадрата) — это отрезок, который соединяет противоположные вершины».

Учитель просит измерить и сравнить по длине диагонали одного

прямоугольника. Каждый ученик измеряет диагонали своего прямо­угольника, а вывод у всех один: диагонали прямоугольника равны

между собой.

К такому же выводу можно подвести учащихся, разрезав не­сколько прямоугольников по диагоналям и совместив полученные

треугольники.

Желательно определить виды углов, образующихся при пере­сечении диагоналей квадрата и прямоугольника (диагонали квад­рата при пересечении образуют прямые углы, а любого другого прямоугольника — два острых и два тупых угла).

Полезно предложить учащимся разрезать сначала квадрат, а потом прямоугольник по одной, а затем по обеим диагоналям и сравнить путем наложения полученные треугольники. На основании проделанной работы, наблюдений учащиеся должны сделать выводы о форме и размерах полученных — сначала двух, а потом и четы­рех — треугольников. Такого рода упражнения играют огромную роль в развитии учащихся вспомогательной школы, так как в этом случае происходит формирование практической и умственной дея­тельности детей.

В III классе учащиеся знают, что в прямоугольнике (квадрате) есть противоположные стороны. Они лежат друг против друга и не имеют общих точек. А теперь (V класс) учитель показывает и называет смежные стороны. Путем организации наблюдений уча­щихся и наводящих вопросов (как расположены смежные стороны? Имеют ли смежные стороны общие точки?) учащиеся должны сделать посильный для них вывод, какие стороны прямоугольника называются смежными. Учащиеся приводят примеры смежных клас­сов, комнат в квартире.

Для закрепления названия сторон прямоугольника учащимся может быть предложено такое упражнение: из четырех разноцвет­ных планок составить любой прямоугольник. Например, верхнее основание — планка красного цвета, нижнее основание — планка розового цвета, правая боковая сторона — планка зеленого цвета, левая боковая сторона — планка синего цвета. Учитель называет сторону — дети поднимают одну планку, он просит показать противо­положную сторону — дети поднимают другую планку. Учитель просит показать правую боковую сторону, затем стороны, с ней смежные. Сопоставляя противоположные и смежные стороны, учащиеся узнают, что каждая сторона в прямоугольнике (квадрате) имеет только одну противоположную сторону и две смежные.

Поэтому описанная выше работа с цветными планками может быть продолжена. Учитель просит взять розовую планку и положить так, чтобы она была правой боковой стороной, затем взять красную планку и положить так, чтобы она была противоположной ей стороной. Потом достроить фигуру до прямоугольника (квадрата). Новое задание: взять розовую планку — правую боковую сторо­ну, приложить к ней синюю и голубую планки — смежные стороны, достроить до прямоугольника.

Работа с цветными планками выполняется быстро, легко конт-

ролируется учителем (по цвету планок, которые дети по требова­нию учителя поднимают и показывают), все ошибки легко могут быть исправлены.

В VI классе учащиеся знакомятся с высотой прямоугольника. Учитель сообщает учащимся, что в прямоугольнике (квадрате) боковая сторона перпендикулярна основанию (образует с ним пря­мой угол). Боковая сторона прямоугольника (квадрата) называется его высотой.

Прямоугольник

Построение прямоугольника

Уже в первом полугодии IV класса дети должны овладеть приемами вычерчивания любого прямоугольника с помощью чертеж­ного треугольника и линейки на нелинованной бумаге.

Учитель сначала просит сделать чертеж квадрата от руки и проверить, какая получилась геометрическая фигура. Дети измеряют стороны четырехугольника, устанавливают виды углов. Построенный четырехугольник вряд ли будет квадратом. Учитель сообщает, что для построения любого прямоугольника (квадрата) необходимо ис­пользовать чертежный треугольник и линейку.

Сначала рассматривается таблица, на которой показан процесс вычерчивания прямоугольника (прямая, на ней выделено нижнее основание прямоугольника, из концов его проведены вверх под пря­мым углом лучи, на которых отложены боковые стороны, концы боковых сторон соединены отрезком).

Дети под руководством учителя показывают на чертеже эле­менты прямоугольника и составляют план построения фигуры (рис. 23):

1) построить произвольную прямую;

2) отложить на ней нижнее основание;

3) принимая его концы за вершины углов, с помощью чертежного треугольника построить прямые углы;

4) на сторонах этих углов от концов нижнего основания от­ложить боковые стороны;

5) концы боковых сторон соединить отрезком.

Учитель должен обратить внимание учащихся на положение чертежа на листе бумаги (надо правильно провести произвольную прямую линию, чтобы будущий чертеж не выходил за пределы страницы, т. е. надо прикинуть расстояние от верхнего края те­тради до произвольной прямой и соотнести его с боковой стороной прямоугольника — оно должно быть больше стороны прямоуголь­ника).

Когда выполнен чертеж, нужно проверить, удовлетворяет ли по­лученная фигура требованиям задания.

Построение квадрата проводится по такому же плану.

Вычерчивание любого прямоугольника (V класс) по данным размерам сторон выполняется, как и раньше, с помощью чертеж­ного треугольника (рис. 24). Но здесь вершины уже обозначаются буквами, и дети учатся их читать, например: прямоугольник АЕОМ и т. п. По требованию учителя они показывают элементы фигуры и называют их. Например: «В прямоугольнике АЕОМ противопо­ложные стороны AM и ЕО, АЕ и ОМ. Сторона AM имеет две смежные стороны: АЕ и МО и т. д. В прямоугольнике имеются диагонали АО и ME (элементы фигур называются и показываются снизу вверх, слева направо, по часовой стрелке)».

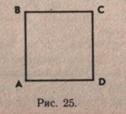
После выполнения чертежа прямоугольника (квадрата) дети де­
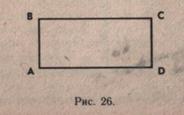
лают запись, поясняющую чертеж (рис. 25 и 26).
AB = BC = CD = DA = 5 cm AB = CD = 5 см

А = B= C= D- BC=AD = 7 см

прямые углы A = B= C= D —

прямые углы

Можно дать обратное задание: A — прямой, А = М = О = К, АМ = МО = ОК = КА=3 см; определить, какая это фигура, а затем выполнить чертеж и еще раз проверить, что он отвечает всем данным задания.

Параллелограмм (ромб)

Впервые с этими видами четырехугольников учащиеся знако­мятся в VII классе. Учитель предлагает школьникам из множества многоугольников отобрать только четырехугольники и объяснить, по каким признакам они это сделали. Затем из четырехугольников он просит выбрать только такие, у которых противоположные сто-

роны параллельны, и говорит, что такие четырехугольники назы­ваются параллелограммами (среди них будут прямоугольники, в том числе квадраты).

Далее рассматриваются элементы параллелограмма: стороны, углы. Учитель просит определить их количество и сообщает, что называние сторон любого параллелограмма такое же, как и сторон прямоугольника. Учащиеся показывают и называют верхнее и нижнее основания, боковые стороны, противоположные и смежные стороны.

Затем каждый ученик на своих моделях параллелограммов, среди которых будут и прямоугольники, должен установить свойства углов путем их совмещения. Учащиеся приходят к выводу, что противоположные углы параллелограммов (прямоугольников) равны.

Далее измеряются стороны параллелограммов (прямоугольни­ков). Оказывается, что в одних параллелограммах только противо­положные стороны равны, а в других — все стороны равны. «Па­раллелограмм, у которого все стороны равны,— сообщает учитель,— называется ромбом». Среди ромбов окажутся и квадраты.

В параллелограммах учащиеся проводят диагонали.

Путем неоднократного измерения устанавливается свойство диа­гоналей параллелограмма.

Высота в параллелограмме (ромбе) проводится внутри фигуры, т. е. из точки (вершины параллелограмма) опускается перпендику­ляр на противоположное основание.

В старших классах, начиная с VII, целесообразно работать над родовыми и видовыми понятиями. С этой целью учитель предла­гает школьникам модели многоугольников и просит: