Проекции прямой. Классификация прямых.

При ортогональном проецировании на плоскость прямая, не перпендикулярная плоскости проекций, проецируется в прямую. В противоположном случае она спроецируется на плоскость в точку.

Для определения проекций прямой достаточно знать проекции двух точек, принадлежащих этой прямой.

Допустим, что даны фронтальные и горизонтальные проекции точек А и В. Проведя через одноименные проекции этих точек прямые линии, получим проекции отрезка АВ в системе π₁, π₂ (рис. 7).

А′′ В′′ - фронтальная проекция отрезка прямой АВ; А′В′ - горизонтальная проекция отрезка прямой АВ.

Рис. 7

Можно утверждать, что такой чертеж (рис. 17) выражает отрезок прямой линии АВ, т.к. если представить себе, что через А′ В′ и через А′′ В′′ проведены проецирующие плоскости (т.е. перпендикулярные соответственно к π₁ и к π₂), то в пересечении этих плоскостей получается прямая и ее отрезок АВ (рис.8).

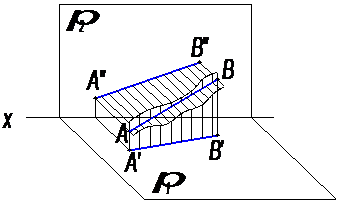
Рис. 8

Проекции прямой могут быть заданы положением относительно осей проекций.

Проекции заданных таким образом прямых обозначаются малыми латинскими буквами (рис. 9 ).

а′′ - фронтальная проекция прямой а; а′ - горизонтальная проекция прямой а.

Рис. 9

Положения прямой

Прямая линия относительно плоскостей проекций может занимать семь положений.

Горизонтальная прямая

Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной. На рисунках 10 изображен отрезок прямой АВ║π₁.

Рис. 10

Следует отметить:

а) горизонтальная проекция горизонтальной прямой равна длине самого отрезка (А′В′ = [AB]);

б) фронтальная проекция горизонтальной прямой параллельна оси проекций х. Если, например, А″В″ совпадает с осью проекций х, то это соответствует положению отрезка АВ в плоскости проекций π₁;

в) угол, образованный горизонтальной проекцией прямой и осью х, равен углу наклона этой прямой к фронтальной плоскости проекций

(А′В′; х=[AB]; π₂=<α^o).

Фронтальная прямая

Прямая, параллельная фронтальной плоскости проекций, называется фронтальной. На рисунках 11 изображен отрезок прямой CD║π₂.

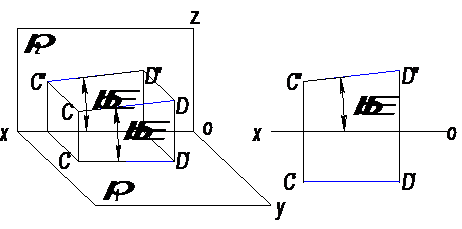
Рис. 11

Для фронтальной прямой следует отметить:

а) фронтальная проекция этой прямой равна длине самого отрезка (С″D″=[CD]);

б) горизонтальная проекция фронтальной прямой параллельна оси х (С′D′║х); Если, например, С′D′ совпадает с осью проекций х, то это соответствует положению CD в пл. π₂.

в) угол, образованный фронтальной проекцией прямой и осью х, равен углу наклона этой прямой к горизонтальной плоскости проекций

(С″D″; х = [CD]; π₁ = <β^о).

Профильная прямая

Прямая, параллельная профильной плоскости проекций, называется профильной. На рисунках 12 изображен отрезок прямой EF║π₃.

Рис. 12

Для профильной прямой характерно:

а) профильная проекция этой прямой равна длине самого отрезка (E″′F″′=[EF]);

б) горизонтальная и фронтальная проекции профильной прямой располагаются на одном перпендикуляре к оси проекций х;

в) Е′′′F′′′; у = [EF]; π₁= <α^о. Е′′′F′′′; z = [EF]; π₂= <β^о

Прямые, параллельные одной плоскости проекций, т.е. горизонтальные, фронтальные и профильные называются прямыми уровня.