Система двух плоскостей проекций. Эпюр Монжа

Гаспар Монж (1746 – 1818) крупный французский геометр, инженер, общественный и государственный деятель предложил метод, обеспечивающий точность и удобоизмеримость изображений, т.е. возможность точно установить место каждой точки изображения относительно других точек или плоскостей и путем простых приемов определить размеры отрезков линий и фигур.

Изложенный Монжем метод – метод параллельного проецирования (причем берутся прямоугольные проекции на две взаимно-перпендикулярные плоскости проекций), обеспечивающий выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остается основным методом составления технических чертежей.

Рис. 1

На рисунке 1 изображены: π₁- горизонтальная плоскость проекций; π₂- фронтальная плоскость проекций; х – ось проекций; А – точка в пространстве.

Здесь показано построение проекций некоторой точки А в системе π₁, π₂. Проведя из точки А проецирующие лучи S₁ и S₂ перпендикулярно к π₁ и π₂ до пересечения с этими плоскостями, получают проекции точки А: горизонтальную, обозначенную А′, фронтальную, обозначенную А′′.

Проекции точки А получаются расположенными на прямых, перпендикулярных к оси проекций и пересекающих эту ось в одной и той же точке А_х.

Повернув плоскость π₁ вокруг оси проекций х на угол 90^о (рис.2), получим одну плоскость, плоскость чертежа; проекции А′′ и А′ расположатся на одном перпендикуляре к оси проекций (рис. 3) – на линии связи (А′′А′). В результате указанного совмещения плоскостей π₁ и π₂ получается чертеж, который называют эпюр Монжа. Это чертеж в системе двух прямоугольных проекций.

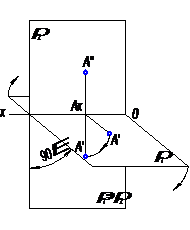
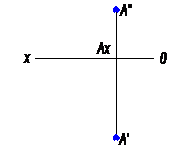
Рис. 2 Рис. 3

При наличии на чертеже оси проекций х положение точки А относительно плоскостей проекций π₁ и π₂ установлено и отрезок А′А_х выражает расстояние точки А от плоскости проекций π₂, а отрезок А′′А_х – расстояние точки А от плоскости проекций π₁.

Две проекции точки вполне определяют ее положение в пространстве относительно данной системы плоскостей проекций.

В системе π₁, π₂ пространство разделено на четыре четверти – I,II, III, IV (рис. 4). Например точка А (рис. 2…3) располагается в первой четверти.

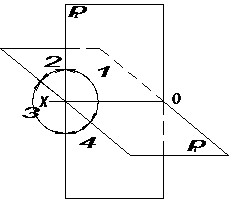
Рис. 4

Таблица 1

Знаки координат в четвертях

Четверть	Знаки координат
x	y	z
I	+	+	+
II	+	-	+
III	+	-	-
IV	+	+	-

Конкурирующие точки

Точки, которые расположены на одном и том же проецирующем луче, т.е. одноименные проекции которых совпадают, называют конкурирующими.

а) горизонтально -конкурирующие точки (рис. 5);

Рассмотрим точки А и В, расположенные на одном проецирующем луче S₁ (S_1┴π₁). Горизонтальные проекции этих точек совпадают (А'≡В').

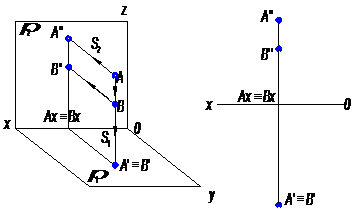
Рис. 5

Точка А закрывает собой точку В при проецировании на плоскость проекций π₁, поэтому ее горизонтальная проекция будет видима, а у точки В – невидима.

б)фронтально – конкурирующие точки (рис. 6);

Рассмотрим точки С и D, расположенные на одном проецирующем луче S₂ (S_2┴π₂). Фронтальные проекции этих точек совпадают (C''≡D'').

Рис. 6

Точка D закрывает собой точку С по отношению к плоскости проекций π₂,поэтому на фронтальной проекции точка С будет невидима, а точка D – видима.