Длины Задачи повышенного уровня
1. Периметр равнобедренной трапеции равен 63, боковая сторона равна большему основанию, а меньшее основание в 2 раза меньше большего. Найдите большее основание.
2. Средняя линия трапеции равна 16, а одно из оснований равно 23. Найдите другое основание трапеции.
3. Диагонали АС и ВD прямоугольника АВСD пересекаются в точке О, АО=12,5, а АВ: ВС=7:24. Найдите СD.
4. Основания трапеции равны 14 и 26. Найдите отрезок, соединяющий середины диагоналей трапеции.
5. В четырёхугольнике АВСD АВ=6, ВС=9, СD =4. Найдите АD , если известно, что в четырёхугольник АВСD можно вписать окружность.
6. Радиус окружности, описанной около равнобедренного прямоугольного треугольного треугольника, равен 34, Найдите катет этого треугольника.
7. К окружности с центром О проведены две касательные, которые пересекаются в точке К, а В и С – точки касания. КО=20,5, а КВ = 20. Найдите радиус окружности.
8. На одной прямой на равном расстоянии друг от друга стоят три телеграфных столба. Крайние находятся от дороги на расстояниях 12м и 32 м. Найдите расстояние, на котором находится от дороги средний столб.
9. .Докажите, что медианы, проведённые к боковым сторонам равнобедренного треугольника, равны.
10. Докажите, что диаметр, проведённый через середину хорды окружности, перпендикулярен ей.
11. Докажите, что если в равнобедренную трапецию можно вписать окружность, то высота равна средней линии.
12. Последовательно соединили отрезками середины сторон четырёхугольника. Докажите, что полученный четырёхугольник является прямоугольником.
13. В окружности проведены две взаимно перпендикулярные хорды. Каждая из них делится другой хордой на отрезки, равные 4 и 6. Найдите расстояние от центра окружности до каждой хорды.
14. Основания трапеции равны 44 и 16, а боковые стороны равны 17 и 25. Найдите высоту трапеции.
15. На боковой стороне АВ равнобедренного треугольника ,как на диаметре, построена окружность. Окружность пересекает основание АС в точке М и боковую сторону СВ в тоске Н. Найдите периметр треугольника МНС, если АВ=10, АС=8.
Тема: Длины Вариант 1
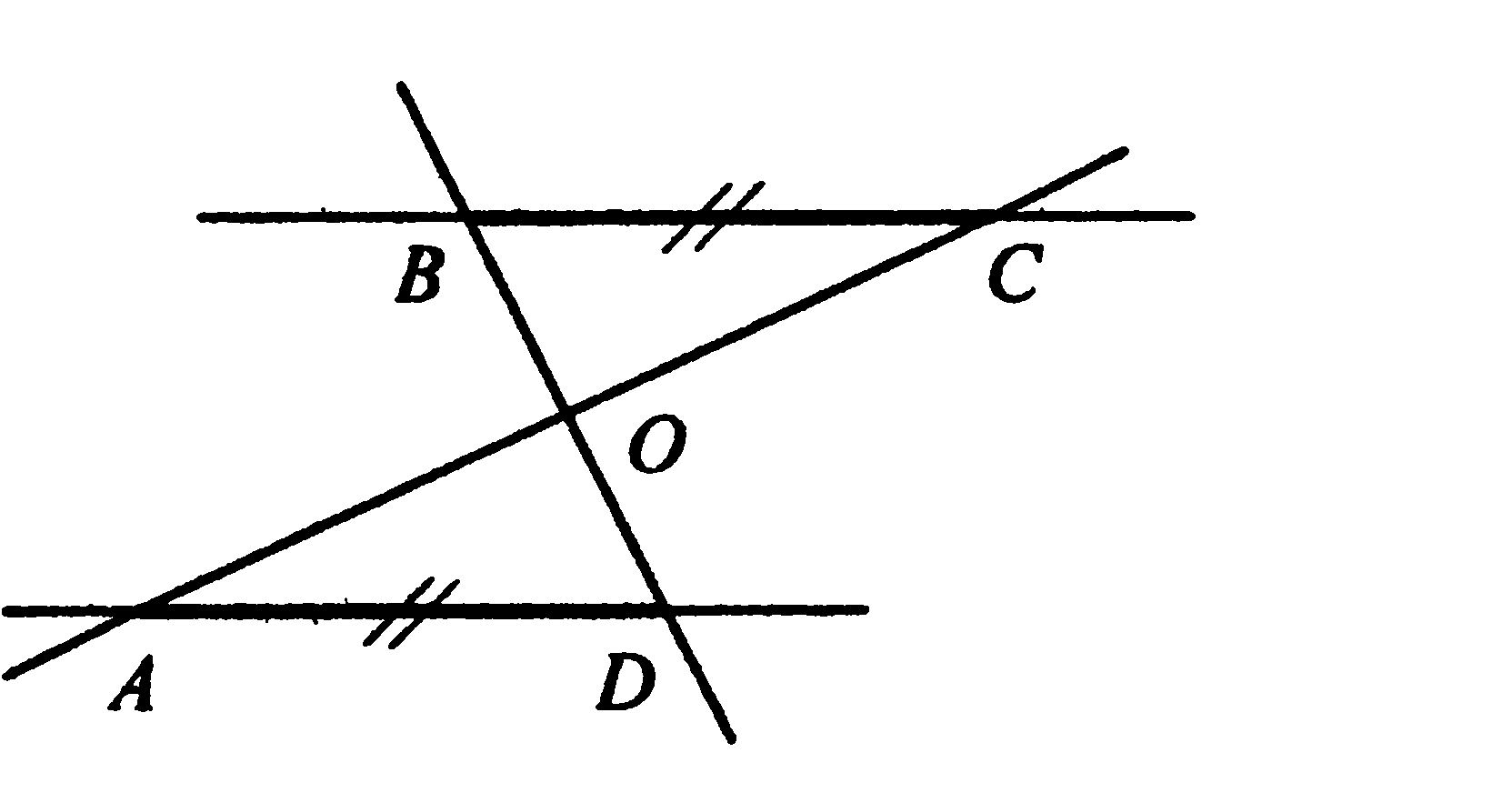
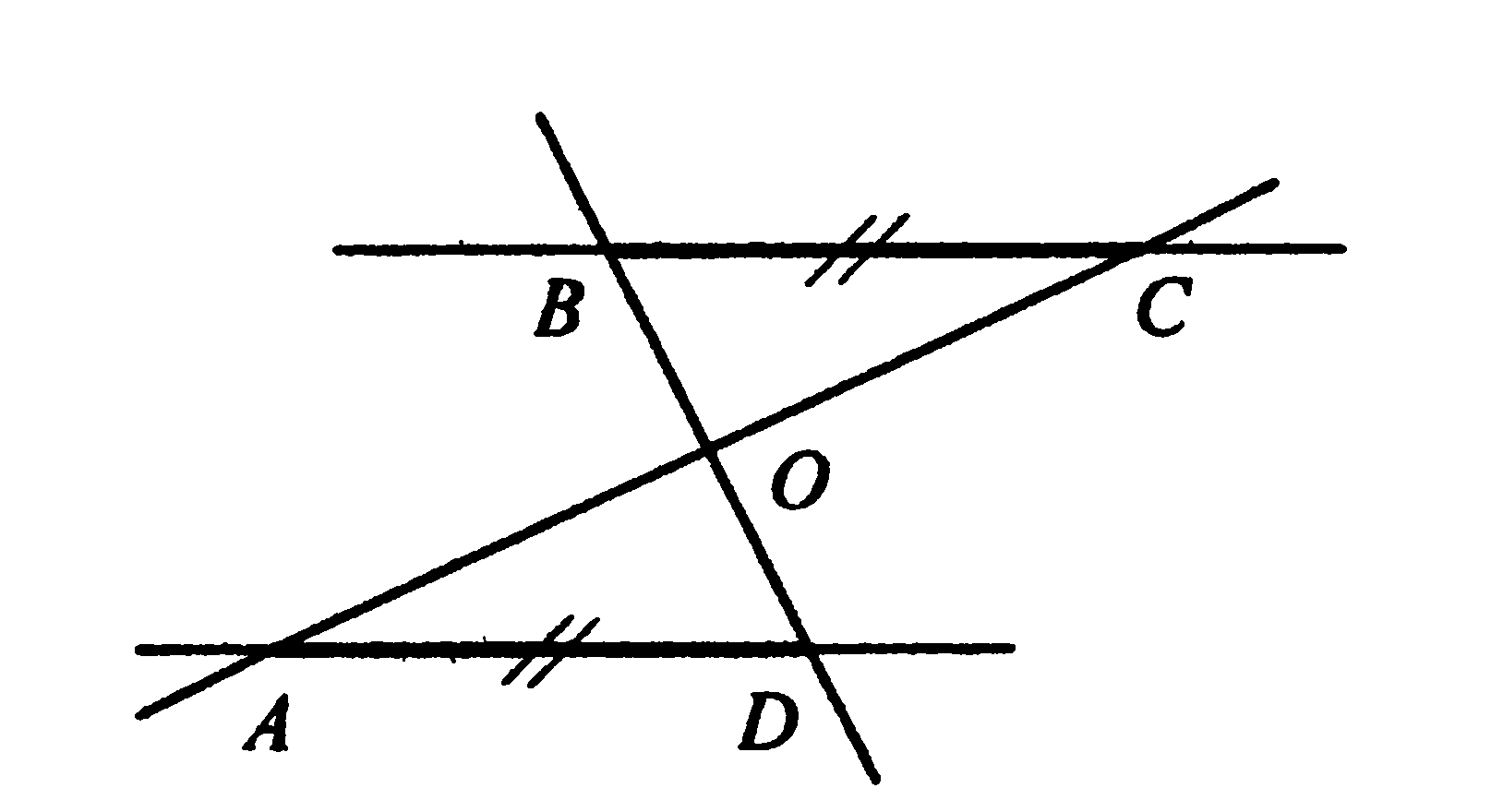
1. Прямые АС и BD пересекаются в точке О. Отрезки ВС и AD лежат на параллельных прямых. Найдите АС, если АО=9.
2. Периметр равностороннего треугольника АВС равен 24см. Найдите длину средней линии этого треугольника.
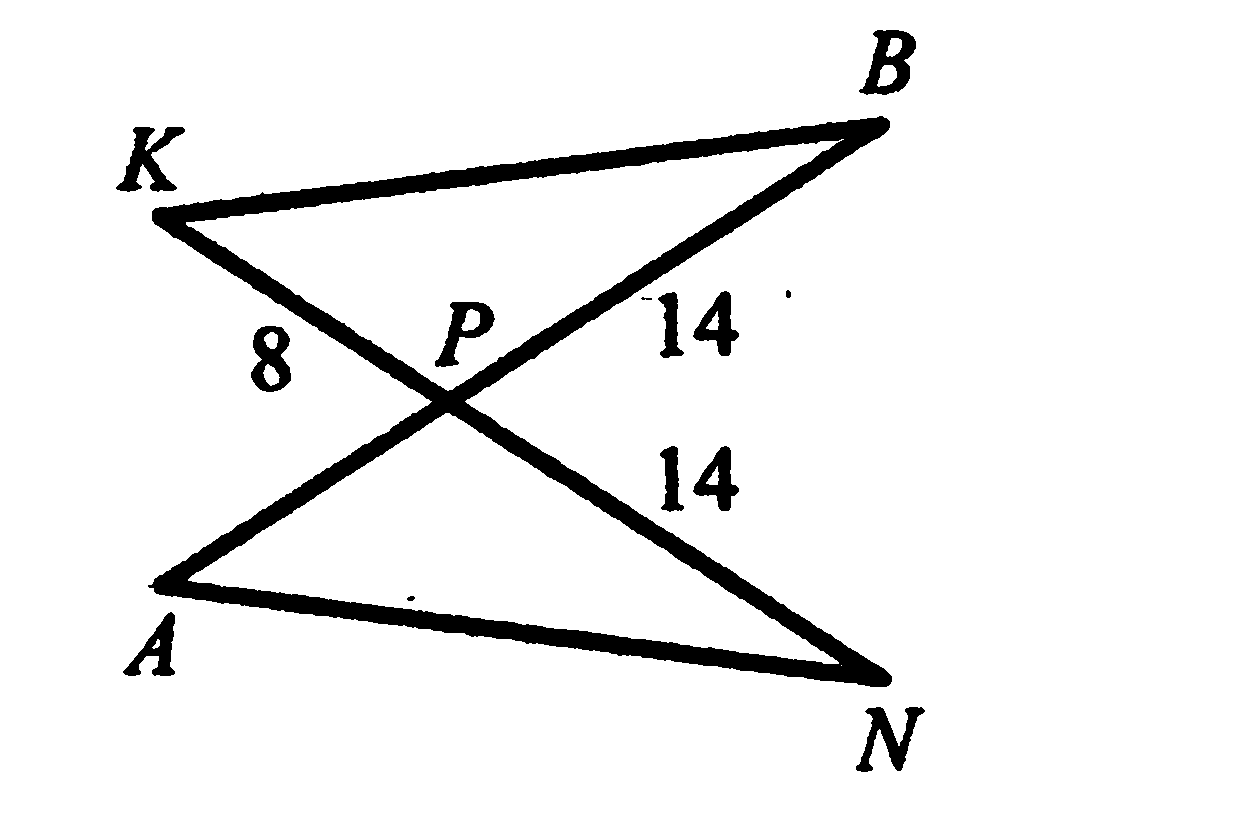
3. Отрезки АВ и KN пересекаются в точке Р, угол ANP равен углу КВР, а КР=8. Найдите длину отрезка АВ.
4. Дан треугольник со сторонами 6, 8 и 10. Найдите периметр треугольника , вершинами которого являются середины сторон данного треугольника
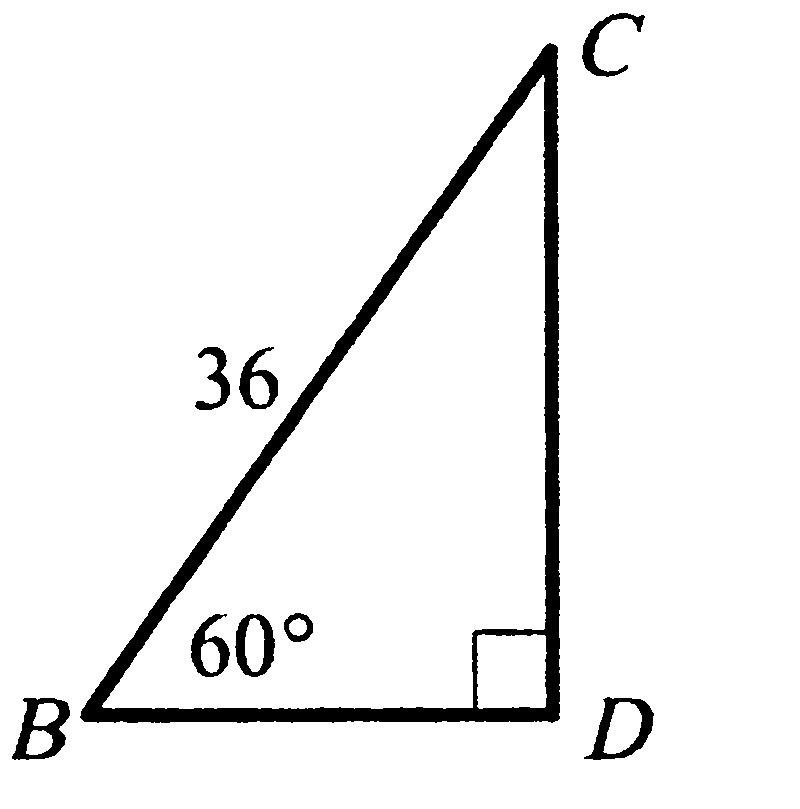
5. Используя данные, указанные на рисунке, найдите катет CD.
1) 18 2) 12  3) 18
3) 18 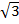 4)18
4)18 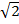 .
.
Тема: Длины Вариант 2
1. Прямые АС и BD пересекаются в точке О. Отрезки ВС и AD лежат на параллельных прямых. Найдите АС, если ОС=7.
2. Периметр равностороннего треугольника АВС равен 36см. Найдите длину средней линии этого треугольника.
3. Отрезки ВС и МK пересекаются в точке О, угол ВМО равен
углу КСО , а ОК=13. Найдите длину отрезка ВС.
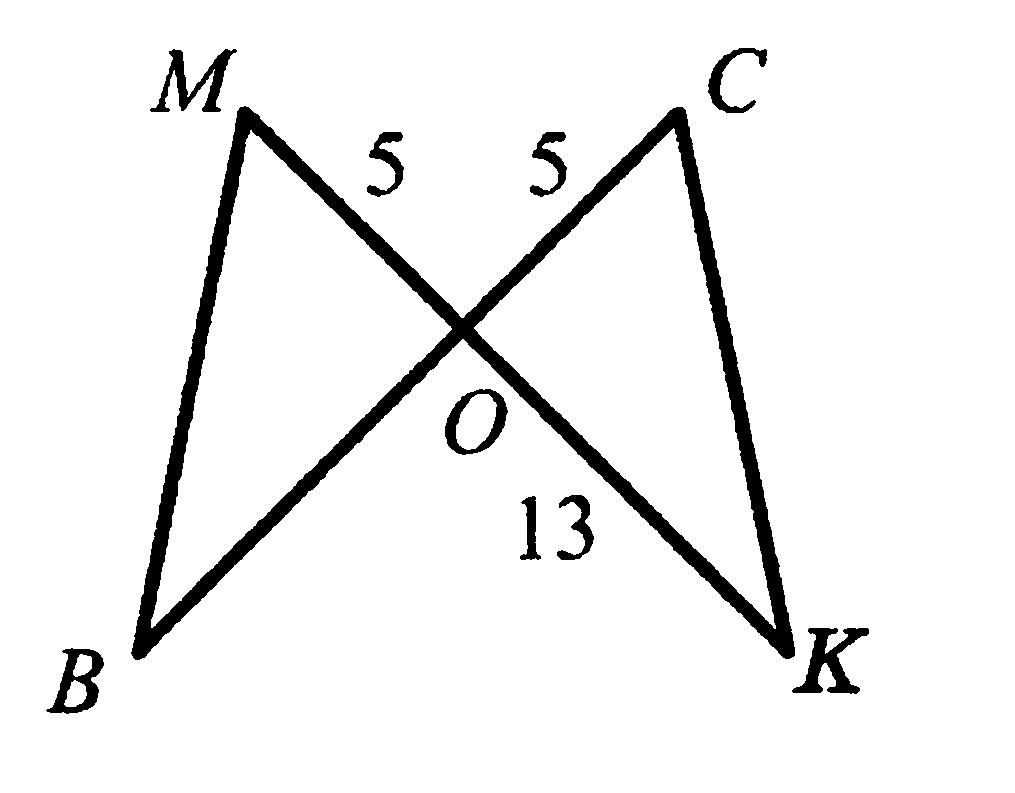
4. Дан треугольник со сторонами 5, 12 и 13. Найдите периметр треугольника , вершинами которого являются середины сторон данного треугольника
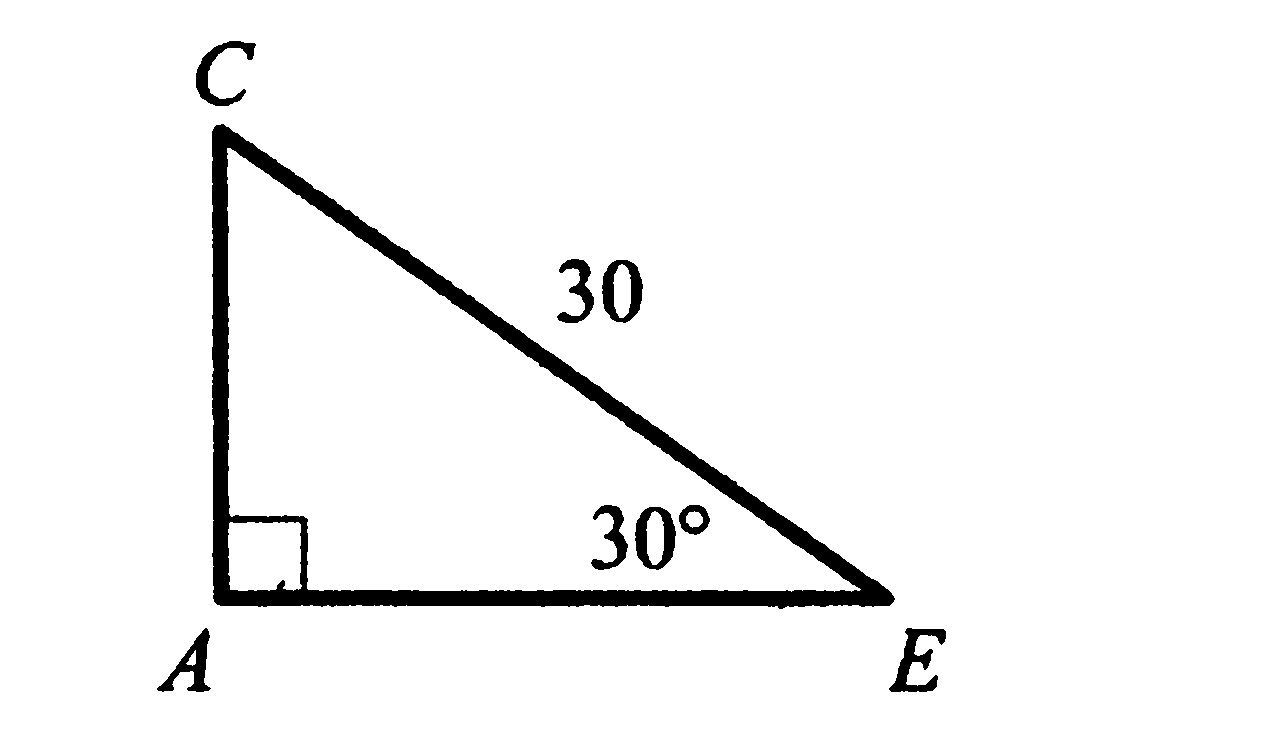
5. Используя данные, указанные на рисунке, найдите катет АЕ.
1) 15 2) 15  3) 15
3) 15  4)10
4)10  .
.
Тема: Длины Вариант 3
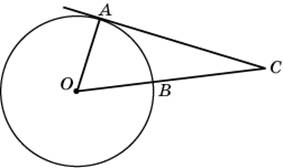
1. К окружности с центром в точке О проведена касательная АC. Точка С удалена от центра окружности на 17см. Найдите длину отрезка ВС, если АС=15см.
2. Сторона ромба равна 20, а острый угол равен 600. Найдите длину меньшей диагонали ромба.
3. В треугольнике АВС угол А прямой, АС=12, cos∠АСВ=0,6.
Найдите ВС.
4. Сторона ромба равна 30, а острый угол равен 600. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Найдите длины этих отрезков.
5. Две стороны параллелограмма равны 10 и 9. Из одной вершины на две стороны опустили высоты, как показано на рисунке. Длина большей из высот равна 6. Найдите длину другой высоты.
10
Тема: Длины Вариант 4
1. К окружности с центром в точке О проведена касательная АC. Точка С удалена от точки касания на 9см. Найдите радиус окружности, если ВC=3см.

2. Сторона ромба равна 32, а острый угол равен 600. Найдите длину меньшей диагонали ромба.
3. В треугольнике АВС угол А - прямой, АС=12, cos∠АСВ=0,3.Найдите ВС.
4. Сторона ромба равна 24, а острый угол равен 600. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Найдите длины этих отрезков.
5. Две стороны параллелограмма равны 6 и 5. Из одной вершины на две стороны опустили высоты, как показано на рисунке. Длина меньшей из высот равна 4. Найдите длину другой высоты
6
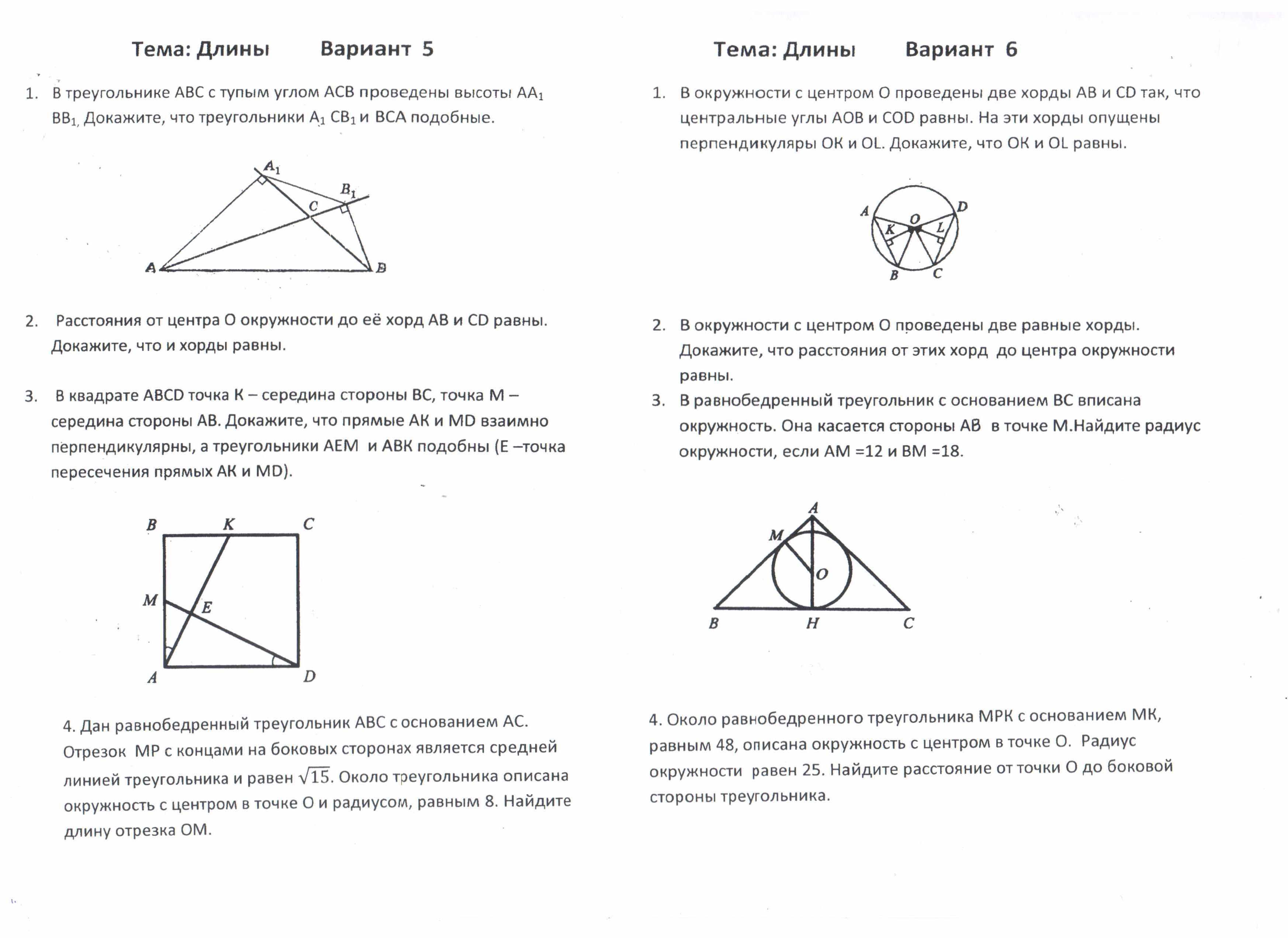
Итоговый тест по теме: Длины Вариант 1
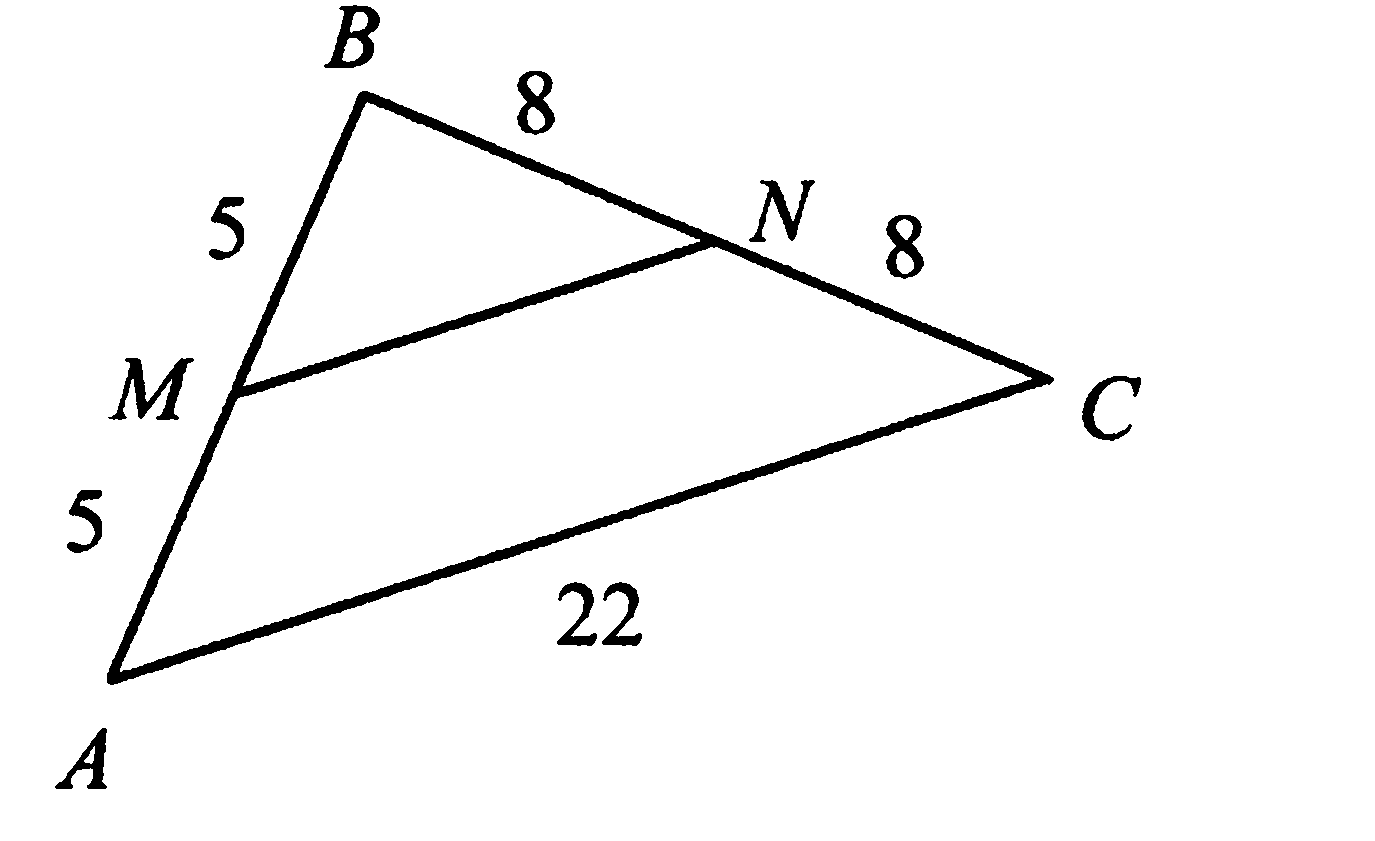
1. Используя данные, указанные на рисунке, найдите периметр треугольника ВМN
2. Найдите длину окружности, радиус которой равен 6
1) 6 π 2) 12π 3) 24 π 4) 36 π
3. Четырёхугольник АВСD – трапеция. Используя данные на рисунке, найдите длину отрезка AD.
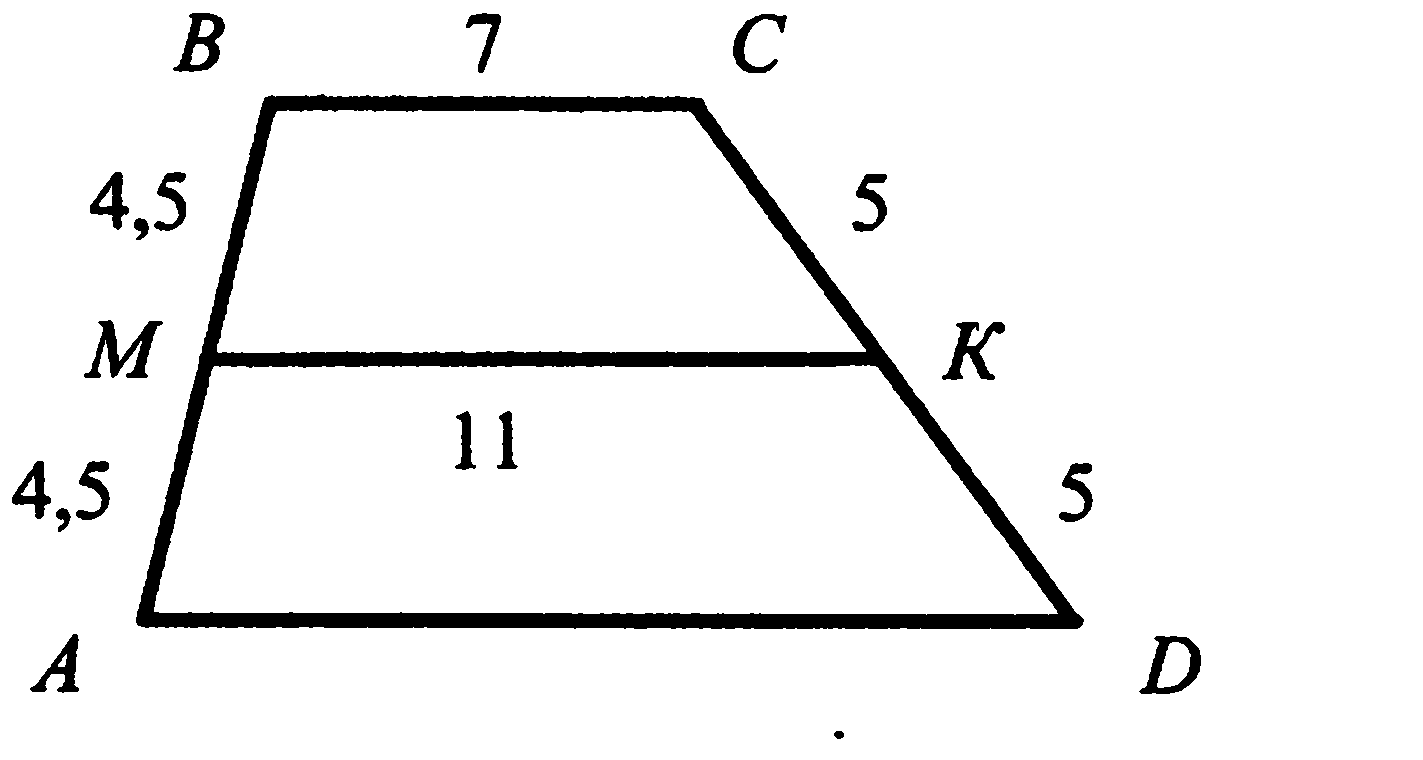
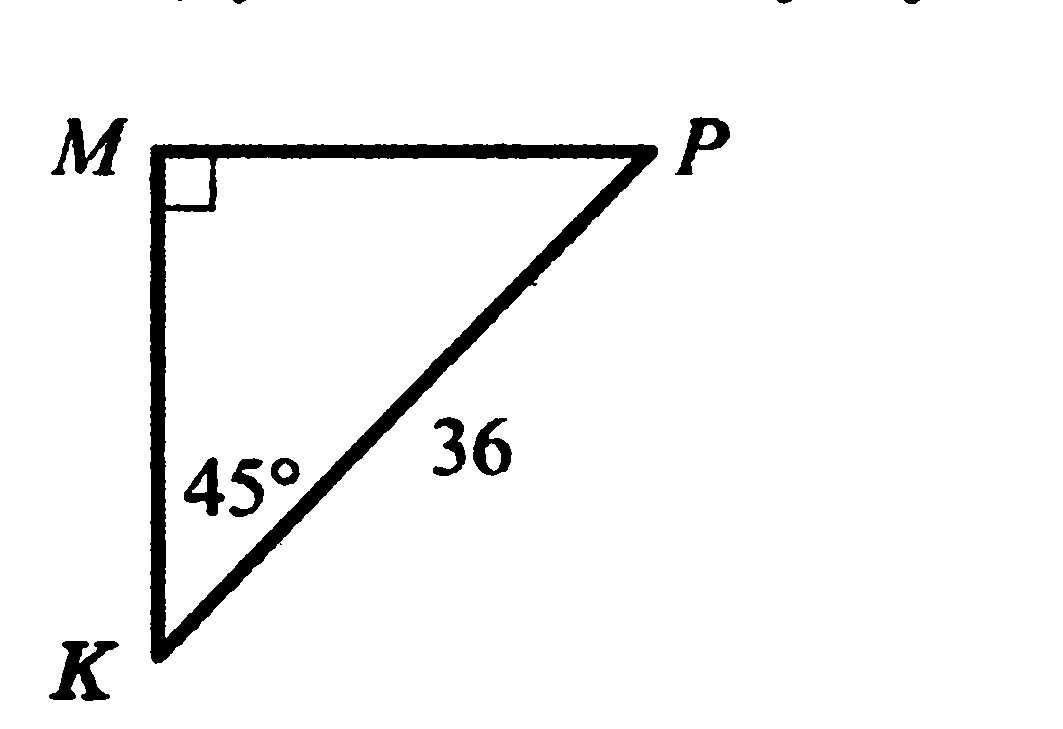
4. Используя данные рисунка, найдите катет PN.
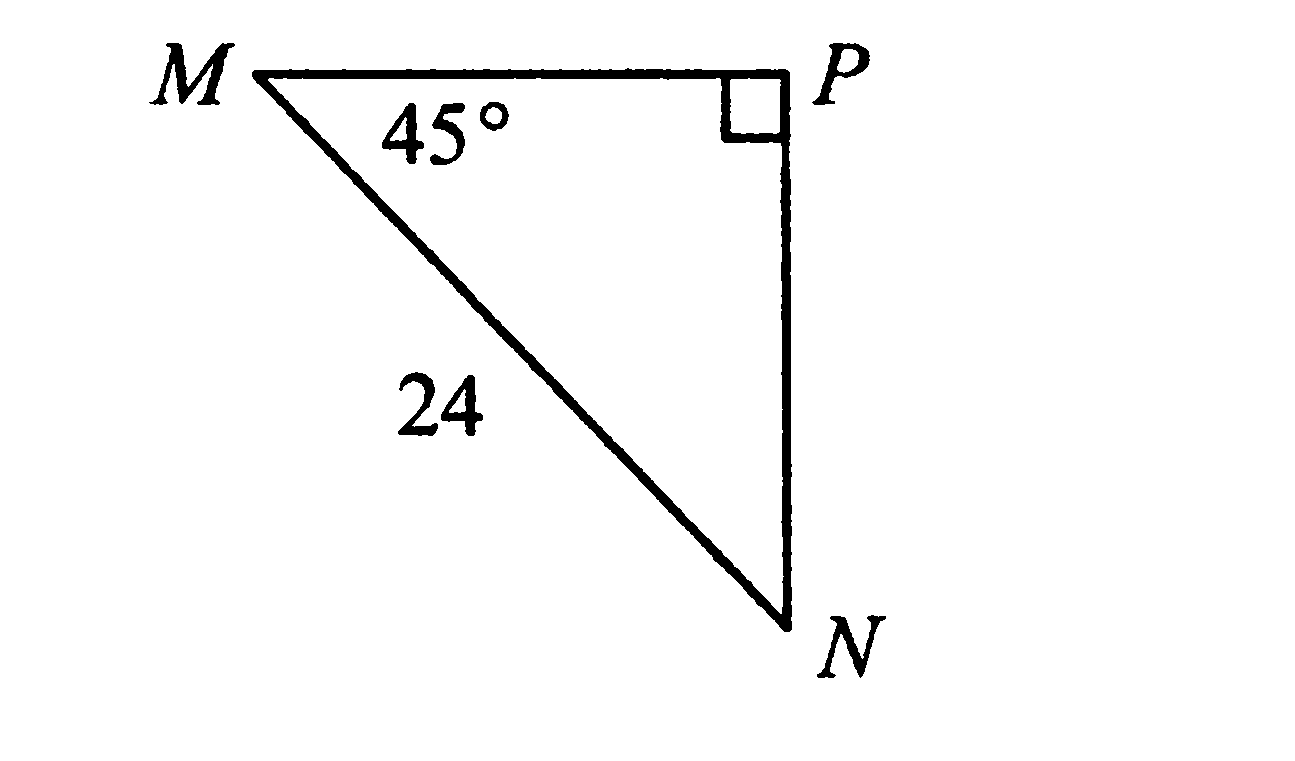 1) 12 3) 12
1) 12 3) 12 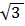
5. Найдите периметр четырёхугольника, если угол АВС равен углу СВD.
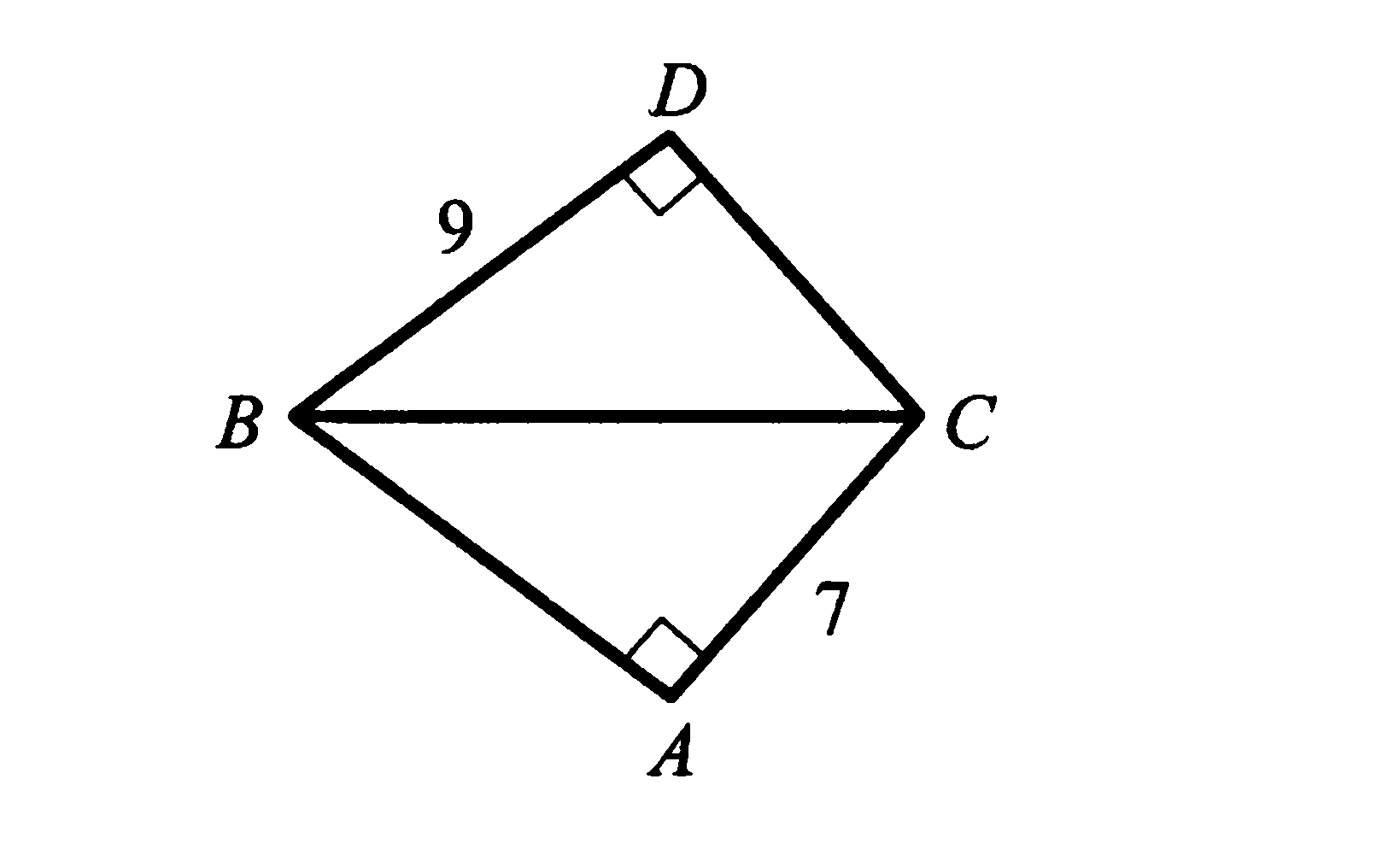
6. На сторонах АС и АВ треугольника АВС отмечены соответственно точки В1 и С1 .Известно, что АВ1 =12 см,
В1С =3см, АС1 =10см, С1В = 8см. Докажите, что треугольники АВС и АВ1С1 подобны.
7. Одна из биссектрис треугольника равна 10 см и делится точкой пересечения биссектрис в отношении 3:2, считая от вершины. Найдите длину стороны треугольника, к которой эта биссектриса проведена, если периметр треугольника равен 2 0см.
2) 12 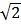 4) 24
4) 24 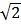
Итоговый тест по теме: Длины Вариант 2
1. Используя данные, указанные на рисунке, найдите периметр треугольника АВС. 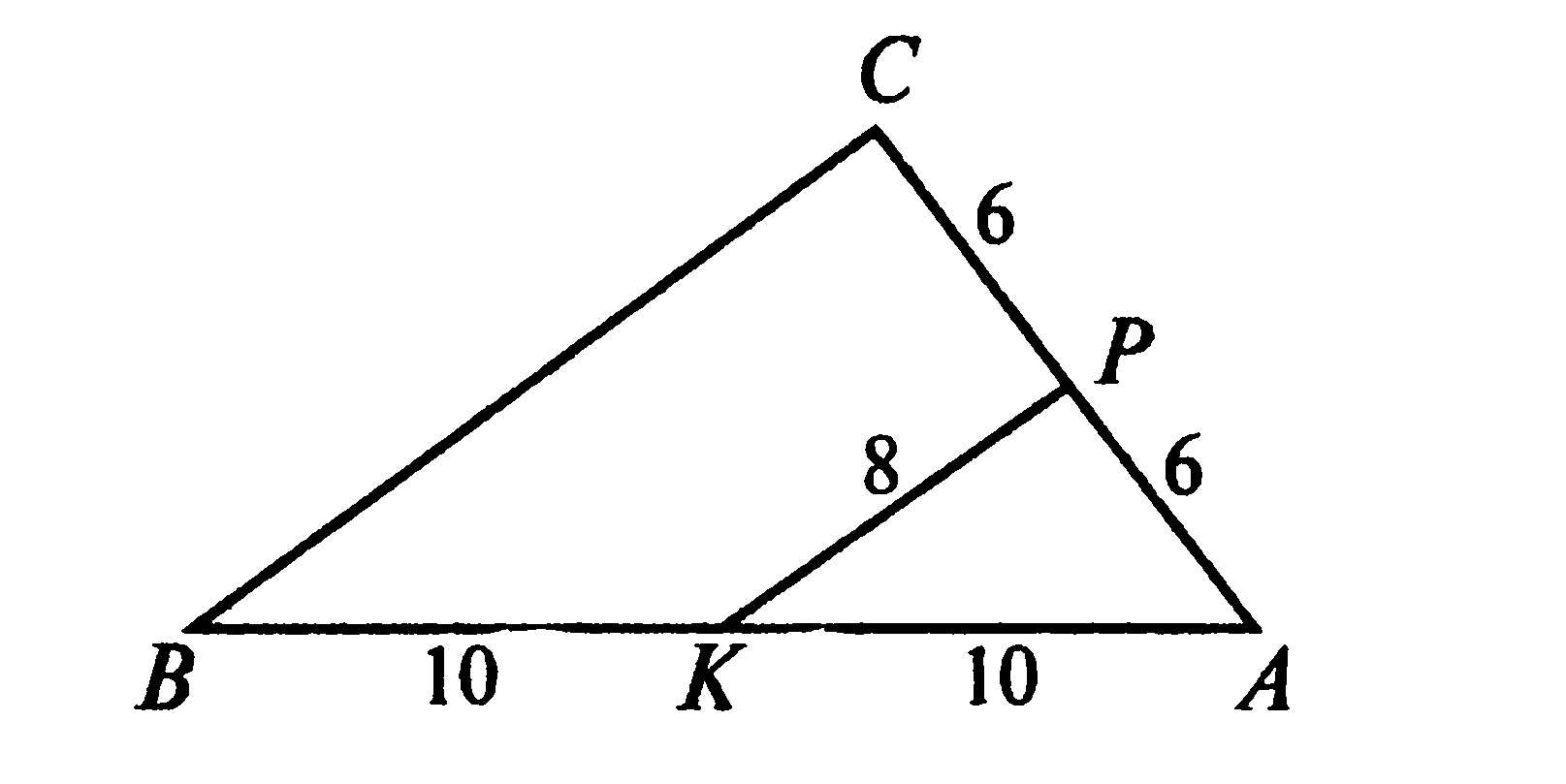
2. Найдите длину окружности, радиус которой равен 8
2) 8 π 2) 16π 3) 32 π 4) 48 π
3. Четырёхугольник АВСD – трапеция. Используя данные на рисунке, найдите длину отрезка AD.

4. Используя данные рисунка, найдите катет МК.
1) 18 2) 36 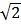 3) 18
3) 18 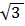 4) 18
4) 18 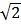
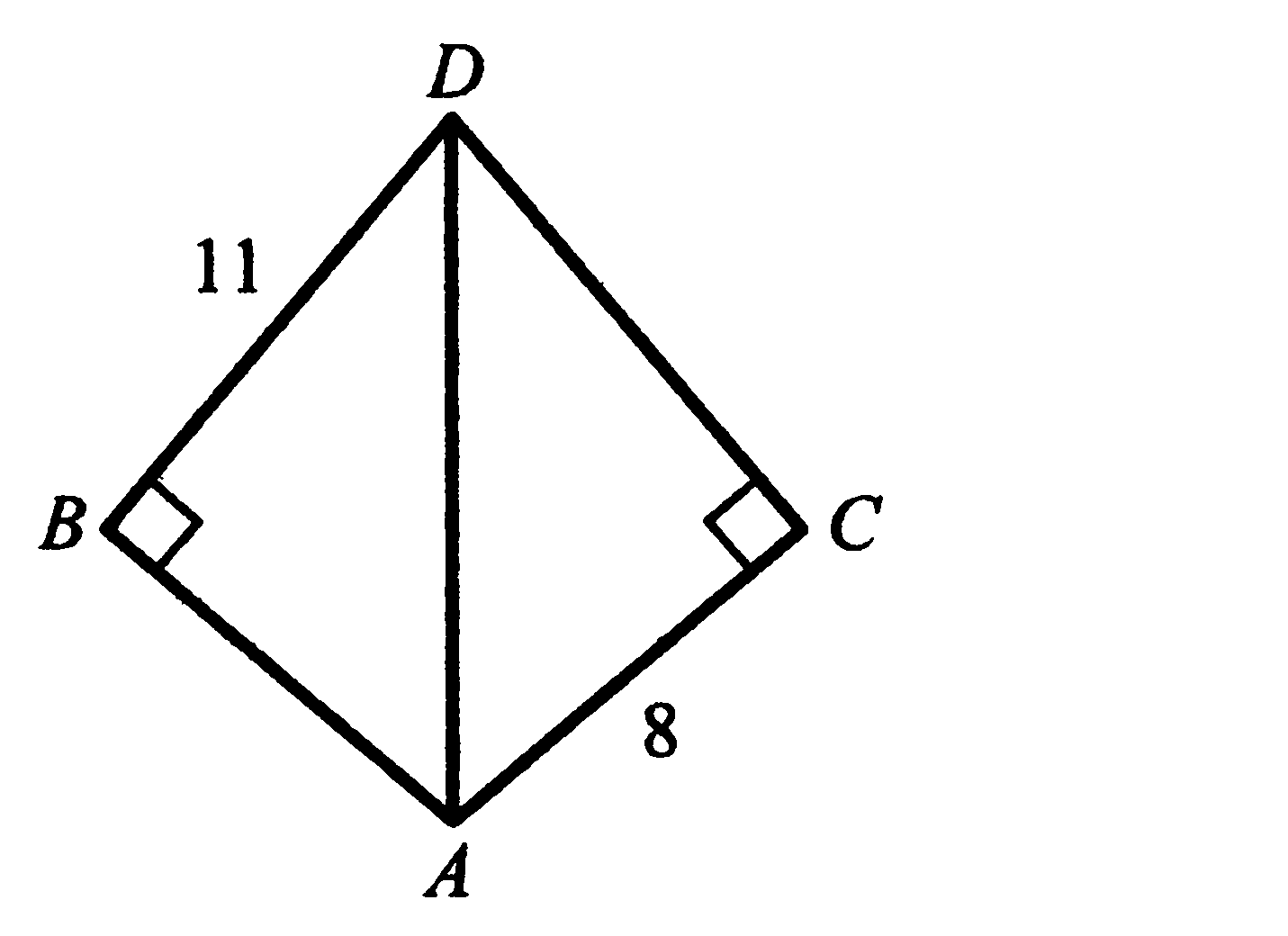
5. Найдите периметр четырёхугольника, если угол ВАD равен углу СAD.
6. На сторонах АС и АВ треугольника АВС отмечены соответственно точки В1 и С1 .Известно, что АВ1 =12 см,
В1С =3см, АС1 = 10см, С1В = 8см. Докажите, что треугольники АВС и АВ1С1 подобны.
7. Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 4:3, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 9 см.