Признаки равенства прямоугольных треугольников
В курсе геометрии 7 класса были изучены, а на прошлом уроке – повторены, так называемые признаки равенства треугольников. Напомним их:
1-й признак (по 2 сторонам и углу между ними): если у треугольников равны две стороны и угол между ними, то такие треугольники равны между собой.
2-й признак (по стороне и двум прилежащим углам): если у треугольников равны сторона и два угла, прилежащие к данной стороне, то такие треугольники равны между собой. Примечание: пользуясь тем, что сумма углов треугольника постоянна и равна 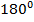 , легко доказать, что условие «прилежания» углов не является необходимым, то есть признак будет верен и в такой формулировке: «… равны сторона и два угла, то …».
, легко доказать, что условие «прилежания» углов не является необходимым, то есть признак будет верен и в такой формулировке: «… равны сторона и два угла, то …».
3-й признак (по 3 сторонам): если у треугольников равны все три стороны, то такие треугольники равны между собой.
Естественно, все эти признаки остаются верными и для прямоугольных треугольников. Однако у прямоугольных треугольников есть одна существенная особенность – у них всегда есть пара равных прямых углов. Поэтому данные признаки для них упрощаются. Итак, сформулируем признаки равенства прямоугольных треугольников:
1-й признак (по двум катетам): если у прямоугольных треугольников катеты попарно равны, то такие треугольники равны между собой (см. Рис. 2).
Дано:


Рис. 2. Иллюстрация первого признака равенства прямоугольных треугольников

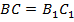
Доказать: 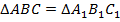
Доказательство: вспомним, что в прямоугольных треугольниках:  . Значит, мы можем воспользоваться первым признаком равенства треугольников (по 2 сторонам и углу между ними) и получить:
. Значит, мы можем воспользоваться первым признаком равенства треугольников (по 2 сторонам и углу между ними) и получить: 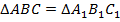 .
.
Доказано.
2-й признак (по катету и углу): если катет и острый угол одного прямоугольного треугольника равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны между собой (см. Рис. 3).
Дано:


Рис. 3. Иллюстрация второго признака равенства прямоугольных треугольников

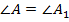
Доказать: 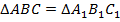
Доказательство:сразу отметим, что тот факт, что равны углы, прилежащие к равным катетам, не является принципиальным. Действительно, сумма острых углов прямоугольного треугольника (по свойству 1) равна  . Значит, если равна одна пара из этих углов, то равна и другая (так как их суммы одинаковы).
. Значит, если равна одна пара из этих углов, то равна и другая (так как их суммы одинаковы).
Доказательство же данного признака сводится к использованию второго признака равенства треугольников (по 2 углам и стороне). Действительно, по условию равны катеты и пара прилежащих к ним углов. Но вторая пара прилежащих к ним углов состоит из углов  . Значит, мы можем воспользоваться вторым признаком равенства треугольников и получить:
. Значит, мы можем воспользоваться вторым признаком равенства треугольников и получить: 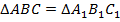 .
.
Доказано.
3-й признак (по гипотенузе и углу): если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны между собой (см. Рис. 4).
Дано:


Рис. 4. Иллюстрация третьего признака равенства прямоугольных треугольников
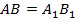
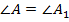
Доказать: 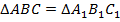
Доказательство:для доказательства этого признака можно сразу воспользоваться вторым признаком равенства треугольников – по стороне и двум углам (точнее, следствием, в котором указано, что углы не обязательно должны быть прилежащими к стороне). Действительно, по условию: 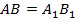 ,
, 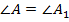 , а из свойств прямоугольных треугольников следует, что
, а из свойств прямоугольных треугольников следует, что  . Значит, мы можем воспользоваться вторым признаком равенства треугольников, и получить:
. Значит, мы можем воспользоваться вторым признаком равенства треугольников, и получить: 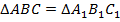 .
.
Доказано.
4-й признак (по гипотенузе и катету): если гипотенуза и катет одного прямоугольного треугольника равны соответственно гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны между собой (см. Рис. 5).
Дано:


Рис. 5. Иллюстрация четвёртого признака равенства прямоугольных треугольников
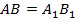

Доказать: 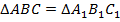
Доказательство:для доказательства этого признака воспользуемся признаком равенства треугольников, который мы сформулировали и доказали на прошлом уроке, а именно: если у треугольников равны две стороны и больший угол, то такие треугольники являются равными. Действительно, по условию у нас есть две равных стороны. Кроме того, по свойству прямоугольных треугольников:  . Осталось доказать, что прямой угол является наибольшим в треугольнике. Предположим, что это не так, значит, должен быть ещё хотя бы один угол, который больше
. Осталось доказать, что прямой угол является наибольшим в треугольнике. Предположим, что это не так, значит, должен быть ещё хотя бы один угол, который больше  . Но тогда сумма углов треугольника уже будет больше
. Но тогда сумма углов треугольника уже будет больше 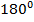 . Но это невозможно, а, значит, такого угла в треугольнике быть не может. Значит, прямой угол является наибольшим в прямоугольным треугольнике. А значит, можно воспользоваться сформулированным выше признаком, и получить:
. Но это невозможно, а, значит, такого угла в треугольнике быть не может. Значит, прямой угол является наибольшим в прямоугольным треугольнике. А значит, можно воспользоваться сформулированным выше признаком, и получить: 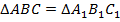 .
.
Доказано.
Сформулируем теперь ещё одно свойство, характерное только для прямоугольных треугольников.
Свойство
Катет, лежащий против угла в  , в 2 раза меньше гипотенузы (см. Рис. 6).
, в 2 раза меньше гипотенузы (см. Рис. 6).
Дано:

Рис. 6.

Доказать:AB 
Доказательство:выполним дополнительное построение: продлим прямую 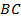 за точку
за точку 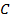 на отрезок, равный
на отрезок, равный 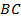 . Получим точку
. Получим точку 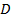 . Так как углы
. Так как углы  и
и 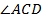 – смежные, то их сумма равна
– смежные, то их сумма равна 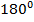 . Поскольку
. Поскольку  , то и угол
, то и угол  .
.
Значит, прямоугольные треугольники  (по двум катетам:
(по двум катетам: 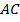 – общий,
– общий,  – по построению) – первый признак равенства прямоугольных треугольников.
– по построению) – первый признак равенства прямоугольных треугольников.
Из равенства треугольников следует равенство всех соответствующих элементов. Значит,  . Откуда:
. Откуда:  . Кроме того,
. Кроме того,  (из равенства всё тех же треугольников). Значит, треугольник
(из равенства всё тех же треугольников). Значит, треугольник  – равнобедренный (так как у него равны углы при основании), но равнобедренный треугольник, один из углов которого равен
– равнобедренный (так как у него равны углы при основании), но равнобедренный треугольник, один из углов которого равен  , – равносторонний. Из этого следует, в частности, что
, – равносторонний. Из этого следует, в частности, что  , что и требовалось доказать.
, что и требовалось доказать.
Доказано.
4. Свойство катета, лежащего против угла в 
Стоит отметить, что верно и обратное утверждение: если в прямоугольном треугольнике гипотенуза в два раза больше одного из катетов, то острый угол, лежащий напротив этого катета, равен  .
.
Сформулируем ещё один важный признак прямоугольного треугольника.
Примечание:признакозначает, что если какое-то утверждение верно, то треугольник является прямоугольным. То есть признак позволяет идентифицировать прямоугольный треугольник.
Важно не путать признак сосвойством– то есть, если треугольник прямоугольный, то у него есть такие свойства… Часто признаки и свойства являются взаимно обратными, но далеко не всегда. Например, свойство равностороннего треугольника: в равностороннем треугольнике есть угол  . Но это не будет признаком равностороннего треугольника, так как не любой треугольник, у которого есть угол
. Но это не будет признаком равностороннего треугольника, так как не любой треугольник, у которого есть угол  , является равносторонним.
, является равносторонним.
Можно привести и более жизненный пример: свойство слова «хлеб» – в слове «хлеб» 4 буквы. Но наличие 4 букв не является признаком слова «хлеб», так как существует множество слов из 4 букв.
5. Признак прямоугольного треугольника (медиана равна половине стороны, к которой проведена)
Итак, признак прямоугольного треугольника:
Если в треугольнике медиана равна половине стороны, к которой она проведена, то данный треугольник является прямоугольным, причём медиана проведена из вершины прямого угла.
Примечание:напомним, что медиана – линия, соединяющая вершину треугольника с серединой противоположной стороны (см. Рис. 7).
Дано:

Рис. 7.

Доказать: 
Доказательство:поскольку  , то треугольники
, то треугольники  – равнобедренные. Значит, углы при основаниях каждого из этих треугольников равны. То есть,
– равнобедренные. Значит, углы при основаниях каждого из этих треугольников равны. То есть,  ,
,  . Тогда сумма углов треугольника
. Тогда сумма углов треугольника 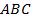 равна
равна  Значит,
Значит,  . Но:
. Но:  , что и требовалось доказать.
, что и требовалось доказать.
Доказано.
В данном уроке мы рассмотрели основные свойства прямоугольных треугольников, изученные ранее в 7 классе. В частности, вспомнили признаки равенства, а также другие признаки и свойства прямоугольных треугольников.
Домашнее задание
1. В прямоугольном треугольнике 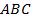
 ,
,  – биссектриса,
– биссектриса,  . Найти длину катета
. Найти длину катета 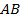 , если
, если  см.
см.
2. На гипотенузе 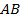 прямоугольного треугольника
прямоугольного треугольника 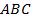 обозначили точку
обозначили точку 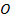 так, что
так, что 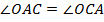 . Докажите, что точка
. Докажите, что точка 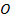 равноудалена от точек
равноудалена от точек 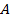 ,
, 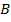 и
и 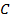 .
.
3. Найти острые углы прямоугольного треугольника, если они относятся как 5:13.
4. Медиана  , проведенная к гипотенузе, равняется
, проведенная к гипотенузе, равняется  см.
см.  .
.
5. В треугольнике 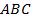
 ,
,  – биссектриса,
– биссектриса,  . Отрезок
. Отрезок  на
на  см меньше отрезка
см меньше отрезка 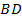 . Найти биссектрису
. Найти биссектрису  .
.
Урок 5: Многоугольники
На этом уроке мы приступим уже к новой теме и введем новое для нас понятие «многоугольник». Мы рассмотрим основные понятия, связанные с многоугольниками: стороны, вершины углы, выпуклость и невыпуклость. Затем докажем важнейшие факты, такие как теорема о сумме внутренних углов многоугольника, теорема о сумме внешних углов многоугольника. В итоге, мы вплотную подойдем к изучению частных случаев многоугольников, которые будут рассматриваться на дальнейших уроках.
1. Понятие «многоугольник»
В курсе геометрии мы изучаем свойства геометрических фигур и уже рассмотрели простейшие из них: треугольники и окружности. При этом мы обсуждали и конкретные частные случаи этих фигур, такие как прямоугольные, равнобедренные и правильные треугольники. Теперь пришло время поговорить о более общих и сложных фигурах – многоугольниках.
С частным случаем многоугольников мы уже знакомы – это треугольник (см. Рис. 1).

Рис. 1. Треугольник
В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник (см. Рис. 2), т.е. фигуру с пятью углами.

Рис. 2. Пятиугольник. Выпуклый многоугольник
Определение. Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.
Определение. Правильный многоугольник– это выпуклый многоугольник, у которого все стороны и углы равны.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят к многоугольнику.
Иными словами, например, когда говорят о пятиугольнике  , имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника, т.е. точка
, имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника, т.е. точка  тоже относится к пятиугольнику (см. Рис. 2).
тоже относится к пятиугольнику (см. Рис. 2).
Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).
Определение. Периметр многоугольника – сумма длин сторон многоугольника.
Теперь надо познакомиться с видами многоугольников. Они делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на Рис. 2, является выпуклым, а на Рис. 3 невыпуклым.

Рис. 3. Невыпуклый многоугольник
2. Выпуклые и невыпуклые многоугольники
Определение 1. Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой. Невыпуклыми являются все остальные многоугольники.
Легко представить, что при продлении любой стороны пятиугольника на Рис. 2 он весь окажется по одну сторону от этой прямой, т.е. он выпуклый. А вот при проведении прямой через 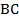 в четырехугольнике на Рис. 3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
в четырехугольнике на Рис. 3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
Но существует и другое определение выпуклости многоугольника.
Определение 2. Многоугольник называется выпуклым, если при выборе любых двух его внутренних точек и при соединении их отрезком все точки отрезка являются также внутренними точками многоугольника.
Демонстрацию использования этого определения можно увидеть на примере построения отрезков 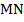 на Рис. 2 и 3.
на Рис. 2 и 3.
Определение. Диагональю многоугольника называется любой отрезок, соединяющий две не соседние его вершины.
3. Теорема о сумме внутренних углов выпуклого n-угольника
Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольника и теорема о сумме внешних углов выпуклого многоугольника. Рассмотрим их.
Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).
 , где
, где  – количество его углов (сторон).
– количество его углов (сторон).
Доказательство 1. Изобразим на Рис. 4 выпуклый n-угольник.

Рис. 4. Выпуклый n-угольник
Из вершины  проведем все возможные диагонали. Они делят n-угольник на
проведем все возможные диагонали. Они делят n-угольник на  треугольника, т.к. каждая из сторон многоугольника образует треугольник, кроме сторон, прилежащих к вершине
треугольника, т.к. каждая из сторон многоугольника образует треугольник, кроме сторон, прилежащих к вершине  . Легко видеть по рисунку, что сумма углов всех этих треугольников как раз будет равна сумме внутренних углов n-угольника. Поскольку сумма углов любого треугольника –
. Легко видеть по рисунку, что сумма углов всех этих треугольников как раз будет равна сумме внутренних углов n-угольника. Поскольку сумма углов любого треугольника – 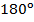 , то сумма внутренних углов n-угольника:
, то сумма внутренних углов n-угольника:
 , что и требовалось доказать.
, что и требовалось доказать.
Доказательство 2. Возможно и другое доказательство этой теоремы. Изобразим аналогичный n-угольник на Рис. 5 и соединим любую его внутреннюю точку со всеми вершинами.

Рис. 5.
Мы получили разбиение n-угольника на n треугольников (сколько сторон, столько и треугольников). Сумма всех их углов равна сумме внутренних углов многоугольника и сумме углов при внутренней точке, а это угол  . Имеем:
. Имеем:
 , что и требовалось доказать.
, что и требовалось доказать.
Доказано.
По доказанной теореме видно, что сумма углов n-угольника зависит от количества его сторон (от n). Например, в треугольнике  , а сумма углов
, а сумма углов  . В четырехугольнике
. В четырехугольнике  , а сумма углов –
, а сумма углов –  и т.д.
и т.д.
4. Теорема о сумме внешних углов выпуклого n-угольника
Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).
 , где
, где  – количество его углов (сторон), а
– количество его углов (сторон), а  , …,
, …,  – внешние углы.
– внешние углы.
Доказательство. Изобразим выпуклый n-угольник на Рис. 6 и обозначим его внутренние и внешние углы.

Рис. 6. Выпуклый n-угольник с обозначенными внешними углами
Т.к. внешний угол связан со внутренним как смежные, то  и аналогично для остальных внешних углов. Тогда:
и аналогично для остальных внешних углов. Тогда:
 .
.
В ходе преобразований мы воспользовались уже доказанной теоремой о сумме внутренних углов n-угольника  .
.
Доказано.
Из доказанной теоремы следует интересный факт, что сумма внешних углов выпуклого n-угольника равна  от количества его углов (сторон). Кстати, в отличие от суммы внутренних углов.
от количества его углов (сторон). Кстати, в отличие от суммы внутренних углов.
Далее мы более подробно будем работать с частным случаем многоугольников – четырехугольниками. На следующем уроке мы познакомимся с такой фигурой, как параллелограмм, и обсудим его свойства.
Домашнее задание
1. Существует ли выпуклый многоугольник, сумма углов которого равна: а)  ; б)
; б)  ; в)
; в)  ?
?
2. Найдите углы четырехугольника, если они пропорциональны числам 2, 3, 10 и 21. Выпуклый или невыпуклый этот четырехугольник?
3. Вершины выпуклого пятиугольника соединены через одну. Найдите сумму углов при вершинах полученной «звезды».
Урок 6: Параллелограмм
Данный урок посвящен одному из видов выпуклых четырехугольников, а именно – параллелограмму. Параллелограмм – один из частных видов четырехугольников, который включает в себя такие подвиды, как прямоугольник, ромб, квадрат – фигуры, с которыми каждый из нас знаком еще с детства. Мы рассмотрим определение и свойства параллелограмма, а также решим несколько примеров с использованием этих свойств.
Определение параллелограмма
На прошлом уроке мы рассмотрели понятие выпуклого многоугольника. Теперь изучим частный случай многоугольника – четырехугольник, а точнее – частный случай четырехугольника – параллелограмм.
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны (см. Рис. 1).
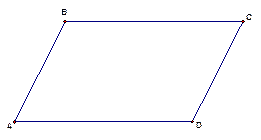
Рис. 1. Параллелограмм
То есть, если даны две параллельные прямые, которые пересекают еще две параллельные прямые, то они образуют фигуру, которая называется параллелограммом  .
.
Из того, что  – параллелограмм, можно сделать следующие выводы:
– параллелограмм, можно сделать следующие выводы: 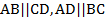 . Верно и обратное утверждение: если
. Верно и обратное утверждение: если 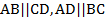 , то четырёхугольник
, то четырёхугольник  – параллелограмм.
– параллелограмм.
Помимо данного определения, можно дать ещё несколько эквивалентных, однако мы остановимся именно на таком, классическом определении параллелограмма, и сформулируем свойства данной фигуры, пользуясь параллельностью её противоположных сторон.
