Кандидат технических наук, доцент А. В. Кострюков
ББК 22.151.3 я 73
Ш37
УДК 514.18 (075.8)
Рецензент
Кандидат технических наук, доцент А. В. Кострюков
Шевченко О.Н., Комиссарова О.Ю.
Ш37 Начертательная геометрия : Учебное
издание.- Оренбург: ОГУ, 2007.- 36 с.
ISBN ……..
В самоучителе рассмотрены правила построения изображений, основанные на методе проекций. Даны базовые понятия и определения курса, проецирование точки, прямой линии, плоскости, решение главных позиционных задач начертательной геометрии.
Учебное издание предназначено для студентов, обучающихся по программам высшего профессионального образования по инженерным направлениям.

 |
ББК 22.151.3 я 73
© Шевченко О.Н., 2002
ISBN …. © ОГУ, 2002
Содержание
| Введение | ………………………………………………………………..………….…….3 | ||||||
| 1 Точка. Прямая. Метод Монжа | ………………….…….………….…………………5 | ||||||
| 2 Точки в четвертях и октантах пространства | …….....………………..…………….7 | ||||||
| 3 Точка в поле проекций | ……...…………………..…………...9 | ||||||
| 4 Прямая общего положения. Следы прямой | ...……………………...……………11 | ||||||
| 5 Определение действительной величины отрезка и углов наклона прямой линии к плоскостям проекций ….............………………… | ……..………12 | ||||||
| 6 Прямые частного положения | ……………………….……………14 | ||||||
| 7 Принадлежность точки прямой линии | ……………………………………16 | ||||||
| 8 Взаимное положение прямых | ………………….…………………19 | ||||||
| 9 Плоскости | ……………………..…………….21 | ||||||
| 10 Прямая и точка в плоскости | ………………….…………………26 | ||||||
| 11 Особые прямые в плоскости | ……………………..…………….28 | ||||||
| 12 Прямая, параллельная плоскости | …………….………….……………29 | ||||||
| 13 Построение взаимно параллельных плоскостей | …………………..……………30 | ||||||
| 14 Пересечение двух плоскостей | ………………….…………………32 | ||||||
| 15 Пересечение прямой с плоскостью | ……………………….…………….37 | ||||||
| 16 О проекциях плоских углов | ……….………….…………………38 | ||||||
| 17 Построение взаимно перпендикулярных прямой и плоскости | ……..…………40 | ||||||
| 18 Построение взаимно перпендикулярных плоскостей | .....………………….……41 | ||||||
| Список использованных источников | …..........................................………45 | ||||||
Введение
Для студентов первый семестр обучения в вузе зачастую становится настоящим испытанием, так как не все первокурсники справляются с учебными программами высшей школы. Это пособие для тех, кто испытывает трудности в изучении начертательной геометрии, кому не понятен текст учебника, кто не успевает осваивать программный материал дисциплины. Учебное издание разработано таким образом, чтобы студент мог самостоятельно преодолеть пробелы в знаниях по элементарной геометрии , освоить базовые понятия и определения курса начертательной геометрии, выработать необходимые навыки решения задач, научиться читать простейшие чертежи. Самоучитель рассчитан на студентов инженерных специальностей и адаптирован к самым разным уровням исходной (базовой) подготовленности обучаемых. "Только тот способ преподавания важен, которым довольны ученики",- эти слова
Л. Н. Толстого подчеркивают необходимость и важность положительного эмоционального тона изложения материала, каким он и является в данном учебном издании.
Точка. Прямая. Метод Монжа
Суть метода Монжа заключается в проецировании различных геометрических единиц - точек, прямых, фигур и поверхностей на две взаимно-перпендикулярные плоскости. Наверняка Вы запомнили рисунок из двух взаимно перпендикулярных плоскостей, одна из которых называется горизонтальной (П1), а другая фронтальной (П2).
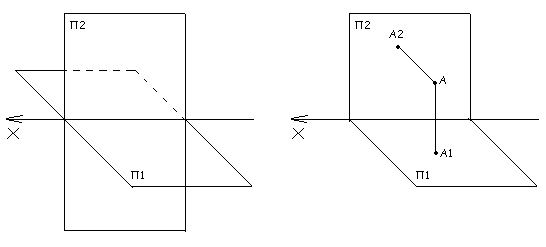
Рисунок 1 Рисунок 2
Проекцию точки А на горизонтальную плоскость проекций получают с помощью проецирующего луча, который проводят через точку А перпендикулярно П1 до пересечения с ней. Точка пересечения называется горизонтальной проекцией точки А и обозначается А1.
Фронтальная проекция точки А получается при пересечении проецирующего луча, проведенного через точку А перпендикулярно П2 и обозначается А2.
Очень часто мы будем рассматривать и профильные проекции точек и прямых. Посмотрите, как располагается профильная плоскость проекций (П3) - она перпендикулярна обеим плоскостям проекций.
Линии пересечения плоскостей проекций называют осями проекций. Всего осей - три: ось ОХ, ось ОУ и ось ОZ. Запомните, пожалуйста, их расположение (рисунок 3).
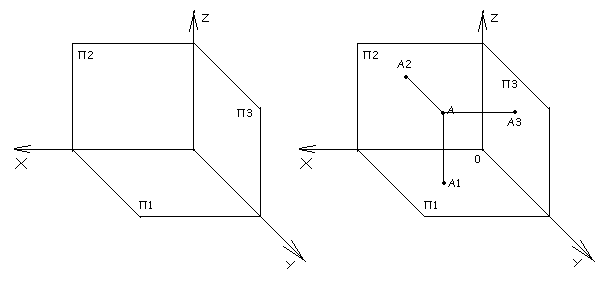
Рисунок 3 Рисунок 4
Если точку А спроецировать на все три плоскости проекций, то получим три проекции точки А – горизонтальную А1, фронтальную А2 и профильную А3 (рисунок 4). Если Вам нужно построить чертеж или эпюр Монжа (это одно и то же) для точки А, то пространственное или наглядное изображение нужно преобразовать в плоскостное. Посмотрите на рисунке 5 как при этом разворачиваются плоскости проекций: фронтальная плоскость остается на месте, горизонтальная опускается вниз до совмещения с фронтальной плоскостью, а профильная разворачивается вправо до совмещения с фронтальной. При этом ось проекций ОУ как бы раздваивается- она участвует в образовании горизонтальной плоскости проекций и необходима для формирования профильной плоскости проекций.
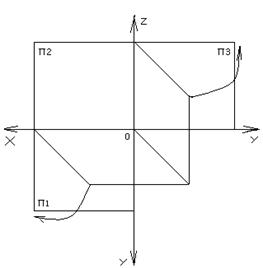
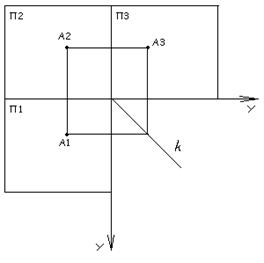
Рисунок 5 Рисунок 6
Таким образом, эпюр точки будет выглядеть как на рисунке 6. Причем, надо обратить внимание на то, что расстояние от точки А до плоскости П1 будет выражаться координатой Z, расстояние от точки А до плоскости П2 будет выражаться координатой У, а до плоскости П3 - координатой Х.
Все три проекции точки взаимосвязаны между собой. Тонкие линии, соединяющие проекции точки А называются линиями связи. Линии связи всегда перпендикулярны осям проекций.
А теперь проверьте себя. Возьмите листок бумаги и постройте чертеж точки А с координатами (15; 30; 10). Координаты даны в мм, т. е. Х=15 мм; У=30 мм; Z=10 мм. Все три проекции должны получиться взаимосвязанными (через них будут проходить линии связи). Попробуйте на этом же чертеже построить точку В (45; 5; 30). Если теперь соединить прямой линией горизонтальные проекции точек А1 и В1 между собой и также поступить с фронтальными проекциями A2 и В2 – получится чертеж прямой (АВ). Самой прямой на чертеже, конечно нет, она изображена с помощью двух своих проекций- горизонтальной А1В1 и фронтальной А2В2. Можно построить и третью проекцию прямой (АВ) - профильную, она будет называться А3В3 и располагаться на профильном поле проекций (Рисунок 7).
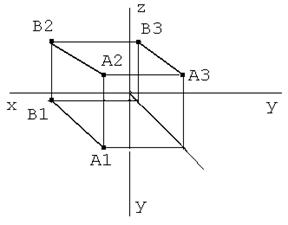
Рисунок 7
Точка в поле проекций
Если у точки одна из трех координат – X, Y или Z равна нулю, то точка будет лежать в горизонтальном, фронтальном или профильном полях проекций. Давайте построим точку А с координатами (0, 15, 40). Наглядное изображение точки с указанием ее проекций можно увидеть на рисунке 11, а эпюр точки А на рисунке 12.
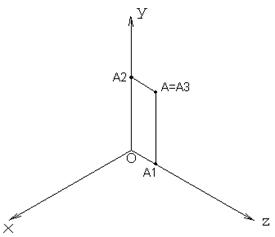
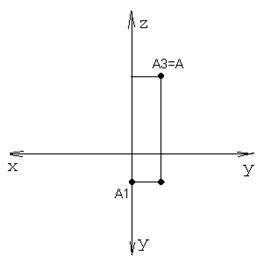
Рисунок 11 Рисунок 12.
Точка лежит в профильном поле проекций и совпадает со своей профильной проекцией. Фронтальная проекция точки А лежит на оси OZ, а горизонтальная на оси OY. Если точка лежит в горизонтальном поле проекций, то ее координата Z должна быть равна нулю. Попробуйте построить, например точку С (20, 40, 0). Проверьте себя по рисунку 13.
Если точка лежит во фронтальном поле проекций, то ее координата Y равна нулю. Для примера построим эпюр точки Т (15, 0, 30) на рисунке 14.
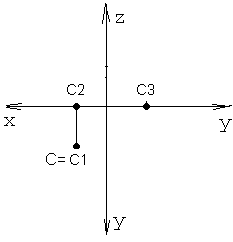
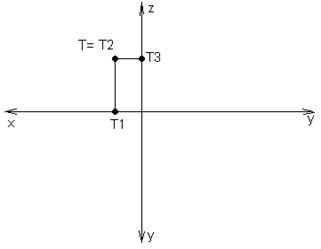
Рисунок 13 Рисунок 14
Иногда точка может лежать сразу в двух плоскостях проекций, например, если точка принадлежит одной из трех осей проекций. Давайте рассмотрим такой вариант. Пусть точка А лежит на оси OZ. Тогда ее координаты Х и Y равны нулю, и только координата Z имеет какое-то значение, например 40. На рисунке 15 выполнено наглядное изображение точки, а эпюр точки А (0, 0, 40) выполнен на рисунке 16. Обратите внимание, что сама точка будет совпадать со своей фронтальной и профильной проекцией, а горизонтальная проекция точки А1 совпадет с началом координат.
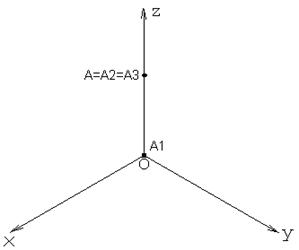
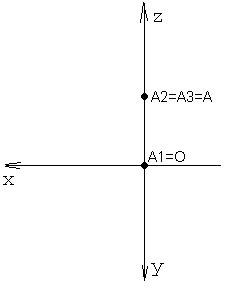
Рисунок 15 Рисунок 16
Эпюр точки, лежащей на оси ОY можно посмотреть на рисунке 17, а эпюр точки, лежащей на оси ОХ на рисунке 18. Попробуйте самостоятельно построить эпюры точек S (0, 25, 0), Т (45, 0, 0). Сравните их с рисунками 17 и 18. Какая из этих точек, по-Вашему, лежит на оси OY, какая на оси ОХ ?
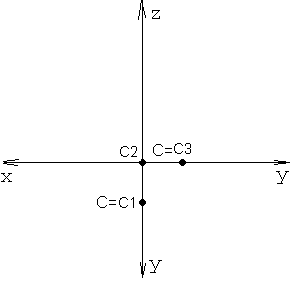
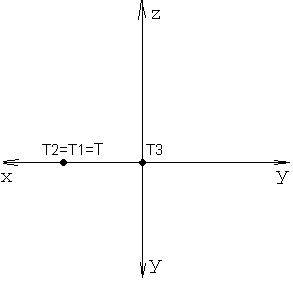
Рисунок 17 Рисунок 18
Прямые частного положения
А нам с вами горизонтальная линия уровня будет очень часто нужна для решения задач. Прямые, параллельные одной или двум плоскостям проекций называются прямыми частного положения.
Прямые, параллельные одной плоскости проекций, называются линиями уровня. Прямая, параллельная горизонтальной плоскости проекций называется горизонтальной прямой уровня. Заметили, что в определении два одинаковых слова? Если прямая параллельна П1, то фронтальная проекция этой прямой параллельна оси проекций ОХ, а горизонтальная проекция отрезка этой прямой равна по величине самому отрезку А1В1 = АВ. Чтобы отличать эту прямую от других, ее, как правило, обозначают буквой h. Посмотрите на рисунке 24, как горизонтальная прямая строится на эпюре. По чертежу можно определить угол наклона горизонтальной прямой к фронтальной плоскости проекций β. Попробуйте самостоятельно в тетради построить третью проекцию прямой h3 по точкам А и В. Оси OZ и OY проведите вертикально в любом месте чертежа. Профильная проекция А3В3 должна получится параллельной оси OY.

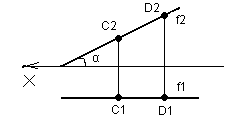
Рисунок 24 Рисунок 25
На рисунке 25 построена прямая линия, которую называют фронтальной прямой и обозначают, как правило буквой f. Фронтальная прямая параллельна фронтальной плоскости проекций, поэтому отрезок такой прямой проецируется в натуральную величину на П2. Угол наклона этой прямой к горизонтальной плоскости проекций обозначен на чертеже через α.
Попробуйте в тетради построить чертеж фронтальной линии уровня, проходящей через точки С (45, 20, 20) и D (20, 20, 40). Построив горизонтальную и фронтальную проекцию, сравните ее с рисунок 25 и достройте самостоятельно профильную проекцию (она должна получится параллельна оси OZ).
Третья линия уровня называется профильной прямой. Она параллельна профильной плоскости проекций, и, значит, координата X для всех ее точек будет одной и той же. На рисунке 26 построена профильная линия уровня в трех проекциях и указаны углы наклона ее к плоскостям проекций – α и β.


Рисунок 26 Рисунок 27
Прямые, параллельные двум плоскостям проекций, называются проеци-рующими. На рисунке 27 изображена горизонтально-проецирующая прямая, которая параллельна фронтальной и профильной плоскостям проекций и, соответственно, перпендикулярна горизонтальной плоскости проекций. Отсюда и название - горизонтально-проецирующая, она совпадает с направлением проецирования на горизонтальную плоскость проекций, и поэтому имеет на П1 вырожденную проекцию прямой – точку. Натуральная величина отрезка может быть определена по фронтальной или профильной проекциям.
Прямая, параллельная горизонтальной и профильной плоскостям проекций называется фронтально-проецирующей, она перпендикулярна П2 и проецируется на нее в точку. На рисунке 28 изображена такая прямая, отрезок проецируется в натуральную величину на П1 и П3.
Прямая, параллельная горизонтальной и фронтальной плоскостям проекций называется профильно-проецирующей прямой, она перпендикулярна профильной плоскости проекций П3, рисунок Отрезок проецируется в натуральную величину на фронтальную и горизонтальную плоскости проекций.
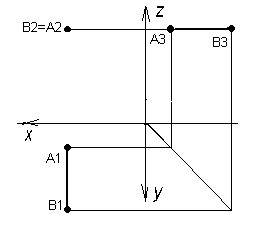

Рисунок 28 Рисунок 29
7 Принадлежность точки прямой линии
Выражение "точка В инцидентна прямой а" означает, что точка В принадлежит прямой а, или что прямая проходит через точку В, или, что тоже самое, точка В лежит на прямой а. Запомните: если точка принадлежит прямой, то ее проекции принадлежат одноименным проекциям этой прямой. Обратное заключение справедливо для всех прямых, кроме профильных уровня. Рассмотрите внимательно рисунок 30 : какая точка принадлежит прямой АВ, а какая нет?
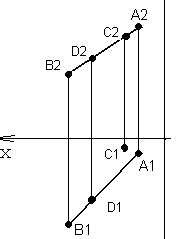
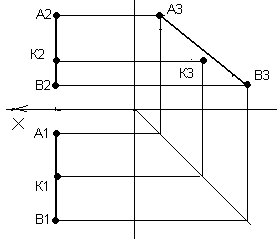
Рисунок 30 Рисунок 31
Проекции точки D лежат на одноименных проекциях прямой АВ, следовательно, точка D принадлежит прямой АВ; Фронтальная проекция точки С принадлежит фронтальной проекции прямой АВ, а горизонтальная проекция С1 не лежит на горизонтальной проекции прямой АВ, следовательно, точка С не принадлежит прямой АВ.
На рисунке 31 изображена профильная прямая CD. Точка К расположена таким образом, что ее горизонтальная проекция К1 принадлежит горизонтальной проекции прямой C1D1, а фронтальная проекция К2 принадлежит фронтальной проекции прямой. Тем не менее, чтобы сделать вывод о принадлежности точки К прямой CD, необходимо построить их третьи проекции – профильные. По чертежу видно, что профильная проекция точки К3 не лежит на профильной проекции прямой, следовательно, и сама точка не принадлежит прямой CD. Для всех других прямых, кроме профильной уровня, достаточно проверить принадлежность двух проекций точки одноименным проекциям прямой.
Взаимное положение прямых
Как известно из программы средней школы, прямые могут пересекаться, быть параллельными (лежать в одной плоскости и не иметь общей точки) и скрещиваться (лежать в разных плоскостях и не иметь общей точки).
Наша задача состоит в том, чтобы разобраться, как изображаются на эпюре параллельные, пересекающиеся и скрещивающиеся прямые. На рисунке 32 изображен эпюр параллельных прямых – одноименные проекции двух параллельных прямых параллельны между собой.
Справедливо и обратное заключение, кроме случая с профильными прямыми. Если даны профильные прямые, то их параллельность проверяется по профильным проекциям.
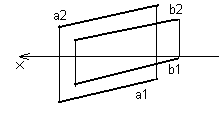
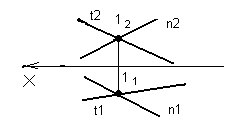
Рисунок 32 Рисунок 33
На рисунке 33 изображены пересекающиеся прямые t (t1, t2) и n (n1, n2). Чертеж пересекающихся прямых показывает, что если прямые пересекаются, то их одноименные проекции пересекаются между собой, а проекции точки пересечения лежат на одной линии связи.
Скрещивающиеся прямые – прямые, которые не пересекаются и не параллельны между собой. На эпюре скрещивающиеся прямые будут напоминать пересекающиеся с той лишь разницей, что точки пересечения фронтальных и горизонтальных проекций не будут лежать на одной линии связи (перпендикуляре к оси ОХ), рисунок 34. В связи с этим вводится понятие конкурирующие точки.
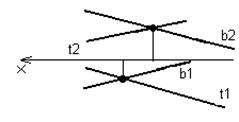
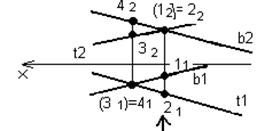
Рисунок 34 Рисунок 35
Точки, лежащие на одном проецирующем луче, называются конкурирующими.
На рисунке 35 обозначены конкурирующие точки и определена их видимость на П1 П2, невидимые точки берутся в скобки. Давайте рассмотрим подробно. На фронтальной проекции пересекаются фронтальные проекции прямых t2 и b2. Обозначим эту точку 1 с индексом 2 и 2 с индексом 2. Допустим, что в пространстве точка 1 лежит на прямой b, а точка 2 на прямой t. Обозначим в соответствии с этим горизонтальные проекции точек 1 и 2. Для определения видимости точек на фронтальной плоскости проекций нужно сравнить координаты Y точек 1 и 2. Координата Y (.) 2 > Y (.) 1, следовательно на фронтальной плоскости проекций точка 2 будет видимой, а точка 1 будет лежать на одном проецирующем луче с точкой 2 и окажется "прикрытой" точкой 2, т. е. невидимой глазу наблюдателя. Такие точки берутся в круглые скобки. На горизонтальной плоскости проекций пересекаются горизонтальные проекции прямых в точке, которую обозначим цифрой 3 с индексом 1 и цифрой 4 с индексом 1. Эти две точки в пространстве лежат на разных прямых, допустим точка 3 на прямой t, а точка 4 на прямой b. Обозначим соответственно этому допущению фронтальные проекции точек. Чтобы определить видимость точек на горизонтальной плоскости проекций нужно сравнить координаты Z этих точек. Координата Z (.) 4 > Z (.) 3, следовательно, на горизонтальной плоскости проекций будет видна точка 4, а точка 3 будет находиться под ней, и ее нужно взять в скобки. Попробуйте по рисунку 35 проговорить этот текст и объяснить себе это несколько раз. Определение видимости по конкурирующим точкам в течение учебного курса пригодится неоднократно.
Плоскости
Из программы средней школы известно, что плоскость в пространстве определяется тремя точками, не лежащими на одной прямой ( прямой и точкой не принадлежащей ей, двумя параллельными прямыми, двумя пересекающимися прямыми, отсеком плоской фигуры - треугольником, четырехугольником и т. д.). В соответствии с этим, на комплексном чертеже плоскость может быть изображена проекциями этих геометрических элементов. На рисунке 36 плоскость задана тремя точками А, В, С. На рисунке 32 – параллельными прямыми а и b, на рисунке 33 плоскость задана пересекающимися прямыми t и n. На рисунке 37 плоскость задана треугольником АВС. Это все известные Вам способы задания плоскостей.
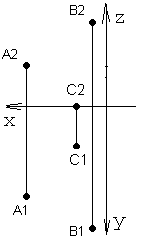

Рисунок 36 Рисунок 37
В начертательной геометрии пользуются еще одним способом задания плоскостей – следами. Следом плоскости называют линию пересечения плоскости с плоскостью проекций. На рисунке 38 дано наглядное изображение плоскости Q, которая пересекается с плоскостями проекций по прямым, называемым следами плоскости. Q1 - горизонтальный след плоскости, Q2- фронтальный след плоскости, Q3 - профильный след плоскости.
Qx, Qy, Qz – точки схода следов на осях проекций. Обычно плоскость на эпюре изображается двумя следами (Q1, Q2), см рисунок 39, которые как две пересекающиеся прямые вполне определяют плоскость. Фронтальный след плоскости расположен во фронтальной плоскости проекций, поэтому его горизонтальная проекция лежит на оси ОХ. Горизонтальный след плоскости расположен в горизонтальной плоскости проекций, поэтому его фронтальная проекция лежит на оси ОХ.
Плоскость, не перпендикулярная ни одной из плоскостей проекций, называется плоскостью общего положения.

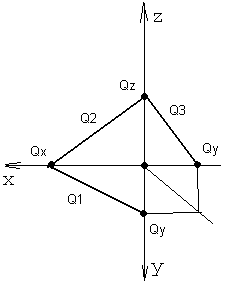
Рисунок 38 Рисунок 39
Плоскость Q – плоскость общего положения, она пересекается со всеми плоскостями проекций, т. к. не параллельна ни одной из них.
Плоскости, перпендикулярные одной какой-нибудь плоскости проекций называются проецирующими.
Плоскость, перпендикулярная горизонтальной плоскости проекций называется горизонтально-проецирующей. Если эта плоскость задана следами, рисунок 40, то ее фронтальный след всегда перпендикулярен оси ОХ, а горизонтальный след составляет с осью ОХ угол β, который является углом наклона данной плоскости к фронтальной плоскости проекций П2.
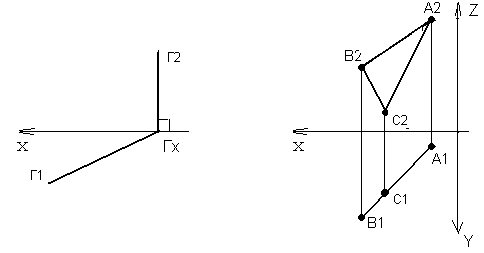
Рисунок 40 Рисунок 41
На рисунке 41 показан эпюр горизонтально-проецирующей плоскости, заданнной треугольником АВС. Так как плоскость перпендикулярна П1, горизонтальная проекция треугольника вырождается в прямую линию.
Плоскость, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей. Если такая плоскость задана следами рисунок 42, то ее горизонтальный след всегда перпендикулярен оси ОХ, а фронтальный составляет с осью ОХ угол α, который является углом наклона данной плоскости к горизонтальной плоскости проекций.
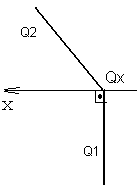

Рисунок 42 Рисунок 43
На рисунке 43 фронтально-проецирующая плоскость задана прямой t и точкой D, не лежащей на этой прямой.
Плоскость, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей.

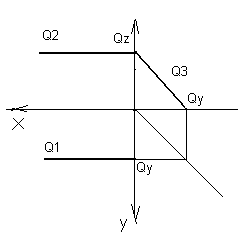
Рисунок 44 Рисунок 45
На рисунке 44 дано наглядное изображение такой плоскости, а на рисунке 45 выполнен эпюр профильно-проецирующей плоскости. Оба следа плоскости, и горизонтальный, и фронтальный, расположены параллельно оси ОХ.
Плоскости, параллельные какой-либо плоскости проекций, называются плоскостями уровня.
Плоскость, параллельная горизонтальной плоскости проекций называется горизонтальной плоскостью уровня. Фронтальный след этой плоскости проходит параллельно оси ОХ, а профильный след – параллельно оси OY. Горизонтального следа у этой плоскости нет, так как она параллельна П1 по определению. На рисунке 46 дано наглядное изображение такой плоскости, а на рисунке 47 ее эпюр. Если плоскость задана треугольником, то он проецируется на горизонтальную плоскость проекций в натуральную величину, см. рисунок 48.

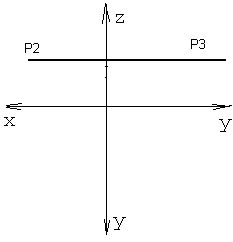
Рисунок 46 Рисунок 47
Плоскость, параллельная фронтальной плоскости проекций называется фронтальной плоскостью уровня. Она не имеет фронтального следа, и все, что в ней лежит, проецируется в натуральную величину на П2. На рисунке 49 фронтальная уровня плоскость задана следами.


Рисунок 48 Рисунок 49
Плоскость, параллельная профильной плоскости проекций называется профильной уровня. Такая плоскость не имеет профильного следа, а ее горизонтальный и фронтальный следы перпендикулярны оси ОХ, рисунок 50. Если плоскость задана геометрической фигурой, то она проецируется в натуральную величину на П3, рисунок 51.


Рисунок 50 Рисунок 51
Прямая и точка в плоскости
Давайте вспомним, когда прямая принадлежит плоскости:
1) прямая принадлежит плоскости, если она проходит через две точки, принадлежащие плоскости;
2) прямая принадлежит плоскости, если она проходит через точку, принадлежащую данной плоскости и параллельна какой-нибудь прямой этой плоскости.
Из этих двух известных Вам признаков принадлежности прямой плоскости можно сделать следующие выводы:
1) если плоскость задана следами, то прямая принадлежит плоскости, если следы прямой лежат на одноименных следах плоскости;
2) прямая принадлежит плоскости, если она с одним следом плоскости имеет общую точку, а другому следу параллельна.
Рассмотрим плоскость Q, общего положения, задана следами, рисунок 52. Прямая NM принадлежит этой плоскости, поскольку ее следы лежат на одноименных следах плоскостей. На рисунке 53 показан эпюр плоскости, заданной пересекающимися прямыми t и n. Чтобы построить прямую, лежащую в этой плоскости, достаточно провести произвольно одну из проекций, например, горизонтальную c1, а затем спроецировть точки пересечения этой прямой с прямыми плоскости на фронтальную плоскость. Фронтальная проекция прямой c2 пройдет через полученные точки.
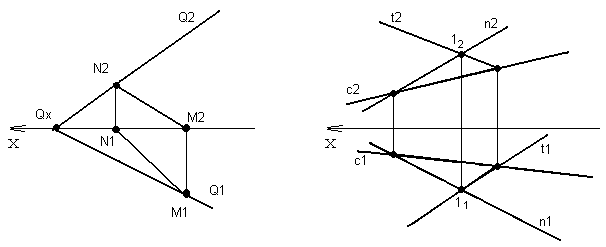
Рисунок 52 Рисунок 53
Согласно второму положению на рисунке 54 построена прямая h, принадлежащая плоскости Р, - она имеет точку N (N1, N2) общую с плоскостью Р и параллельна прямой, лежащей в плоскости - горизонтальному следу Р1.
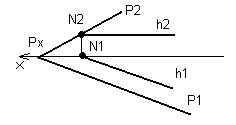
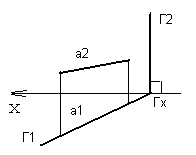
Рисунок 54 Рисунок 55
Рассмотрим плоскости частного положения. Если прямая или фигура принадлежит горизонтально-проецирующей плоскости, то горизонтальные проекции этих геометрических элементов совпадают с горизонтальным следом плоскости.
Если прямая или плоская фигура принадлежит фронтально-проецирующей плоскости, то фронтальные проекции этих геометрических элементов совпадают с фронтальным следом плоскости.
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
ЗАДАЧА 1. Дана плоскость Р (a || b). Известна горизонтальная проекция точки В, принадлежащей плоскости Р. Постройте фронтальную проекцию точки В, рисунок 56. На рисунках 57, 58, 59 показано фрагментарно решение этой задачи: 1) Проведем через В1 (известную проекцию точки В) любую прямую,
лежащую в плоскости Р, - для этого прямая должна иметь с плоскостью две общие точки. Отметим их на чертеже - М1 и K1.
2) Построим фронтальные проекции этих точек по принадлежности точек прямым, т. е. М2 на прямой а, K2 на прямой b. Проведем через фронтальные проекции точек фронтальную проекцию прямой.
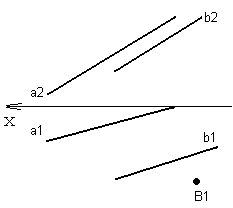

Рисунок 56 Рисунок 57
3) По признаку принадлежности точки плоскости, построим фронтальную проекцию точки В на прямой М2K2.
Т. о. точка В принадлежит плоскости Р так как она лежит на прямой, принадлежащей этой плоскости.

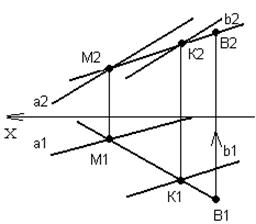
Рисунок 58 Рисунок 59
Особые прямые в плоскости
Пересечение двух плоскостей
Для того, чтобы плоскости пересекались, им достаточно иметь всего одну общую точку.
Но для того, чтобы линию пересечения построить, необходимо найти две точки, общие для обеих плоскостей.
Задача построения линии пересечения плоскостей носит название второй главной позиционной задачи (2ГПЗ) начертательной геометрии. Рассмотрим сначала частные случаи пересечения плоскостей – когда хотя бы одна из плоскостей занимает частное положение по отношению к плоскостям проекций.
ЗАДАЧА: Построить линию пересечения плоскости общего положения, заданной треугольником АВС и плоскостью частного положения Q, заданной следами, рисунок 68.
 Рисунок 68 Рисунок 69
Рисунок 68 Рисунок 69
Решение: Т. к. плоскость Q является горизонтально-проецирующей, то все, что в ней лежит, в том и числе и прямая пересечения с другой плоскостью, имеет свои горизонтальные проекции на горизонтальном следе плоскости Q1. в
данном случае нужно только отметить точки M1 и N1 на сторонах треугольника АВС. Чтобы построить фронтальные проекции этих точек, нужно спроецировать их на соответствующие стороны треугольника на фронтальной плоскости проекций, - N2 на В2С2, а M2 на А2С2.
Линия пересечения заданных плоскостей – NM, рисунок 69.
ЗАДАЧА: Построить линию пересечения плоскостей Р и Г, рисунок 70.
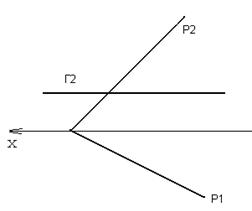
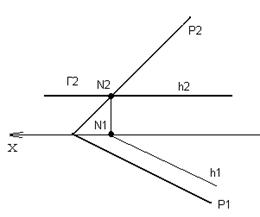
Рисунок 70 Рисунок 71
Решение: Плоскость Р общего положения, а плоскость Г – горизонтальная уровня, следовательно она пересечет плоскость Р по горизонтальной линии уровня. Зная направление горизонтали плоскости Р (ее горизонтальная проекция должна быть параллельна Р1), нам достаточно найти одну общую точку для плоскостей Р и Г. Фронтальные следы плоскостей пересекаются в точке N, горизонтальная проекция этой точки будет лежать на оси ОХ, т. к. точка N лежит во фронтальном поле проекций. Через N1 проведем горизонтальную проекцию горизонтали параллельно Р1, а через N2 – фронтальную проекцию h2, она будет совпадать со следом плоскости Г2. h1, h2 – линия пересечения плоскостей Г и Р.
Рассмотрим общий случай пересечения плоскостей, когда пересекаются плоскости общего положения.
Для решения таких задач запишем последовательность действий:
1. Ввести плоскость – посредник.
2. Построить линии пересечения посредника с каждой из данных плоскостей.
3. Отметить точку пересечения полученных линий.
Таким образом будет построена первая общая точка для двух плоскостей. Чтобы построить еще одну точку, нужно провести еще одну плоскость – посредник и выполнить пункт 2 и 3. Через одноименные проекции построенных точек будет проходить линия пересечения плоскостей.
ЗАДАЧА: Построить линию пересечения плоскостей общего положения, заданных треугольником АВС и следами Г (Г1, Г2), рисунок 72.
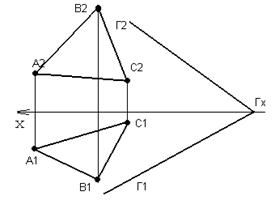
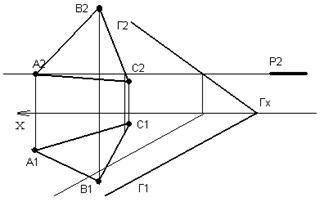
Рисунок 72 Рисунок 73
На рисунке 73 показан первый этап решения задачи – введена вспомогательная плоскость Р, заданная следами, горизонтальная уровня. Она пересекает плоскость треугольника АВС по линии A-1, а плоскость Г по горизонтальной линии уровня h.


Рисунок 74 Рисунок 75
На рисунке 74 показан следующий этап решения – горизонтальные проекции линий пересечения A1, 11 и h1 пересеклись в точке N1. Отметив эту точку, проецируем ее на фронтальную плоскость проекций на линию 12, A2, h2, Р2 (это одна и та же линия, совпадающая со следом плоскости-посредника, ее трудно перепутать с чем-либо, но все же обратите внимание на эту проекцию).
Чтобы построить вторую общую точку, повторим последовательность этих действий еще раз, введя новую вспомогательную плоскость, рисунок 76.
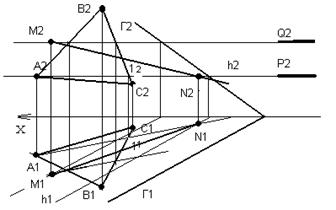

Рисунок 76 Рисунок 77
Линия пересечения плоскостей АВС и Г - прямая MN (M1N1, M2N2).
ЗАДАЧА :
Построить линию пересечения плоскостей Р и Q, общего положения, заданы следами, рисунок 77.
Пересечение горизонтальных следов плоскостей есть их первая общая точка, отметим ее на чертеже M1. Ее фронтальная проекция лежит на оси ОХ, т. к. точка М лежит в горизонтальном поле проекций П1.
Пересечение фронтальных следов плоскости есть их вторая общая точка, отметим ее на чертеже N2. Ее горизонтальная проекция лежит на оси ОХ, т. к. точка N лежит во фронтальном поле проекций П2. M1N1 – горизонтальная проекция линии пересечения, а M2N2 – ее фронтальная проекция.
О проекциях плоских углов
Теорема о проецировании прямого угла очень часто встречается при решении задач, поэтому ее надо обязательно выучить. Итак, попробуем:
Если плоскость прямого угла не перпендикулярна к плоскости проекций и хотя бы одна его сторона параллельна этой плоскости, то прямой угол проецируется на нее в виде прямого же угла.
Давайте разберемся. Мы знаем замечательные прямые, которые параллельны плоскостям проекций. Вспомнили? Конечно, это горизонтальные, фронтальные и профильные линии уровня. Значит, если одной стороной угла будет такая прямая, а другой стороной будет любая прямая общего положения, то можно рассчитывать на проецирование прямого угла без искажения (в натуральную величину) хотя бы на одну плоскость проекций.
Давайте посмотрим на рисунке 82. Сторона СВ прямого угла АСВ параллельна плоскости проекций П1, а сторона АС не перпендикулярна к ней. Тогда проекция прямого угла А1С1В1 будет выглядеть на чертеже тоже как прямой угол.

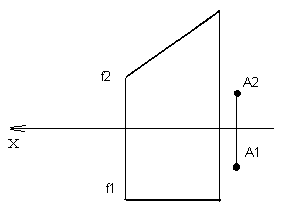
Рисунок 82 Рисунок 83
ЗАДАЧА: Дана фронтальная линия уровня и точка А, не принадлежащая ей. Опустить из точки А перпендикуляр на прямую, рисунок 83.
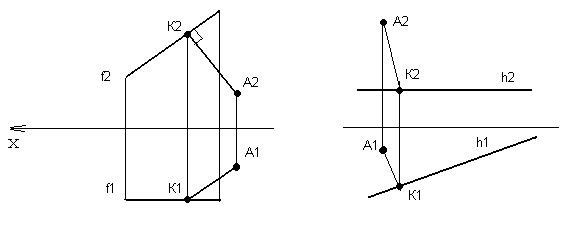
Рисунок 84 Рисунок 85
РЕШЕНИЕ: проведем перпендикуляр через А2 к фронтальной проекции прямой. Точку пересечения перпендикуляра с фронтальной линией уровня обозначим K2, по линии связи построим ее проекцию на горизонтальной проекции фронтали и обозначим ее K1. Таким образом мы получили две проекции перпендикуляра к прямой f, рисунок 84.
Попробуйте решить такую же задачу, только прямая пусть будет горизонтальной линией уровня. На этот раз чертеж будет таким, как на рисунке 85.
Это замечательное свойство проецирования прямого угла мы будем много раз использовать при решении задач. Давайте повторим теорему, не припоминая точной формулировки, а пытаясь вникнуть в суть:
Прямой угол проецируется без искажения на плоскость проекций, если одна его сторона параллельна этой плоскости, а другая не перпендикулярна к ней. Мы это уже проверили на задачах с линиями уровня. Далее эта теорема будет иметь для нас практическое значение именно при построении прямых углов к горизонталям и фронталям.
Точка на поверхности
Пирамида имеет в основании правильный многоугольник, вписанный в окружность диаметром 45 мм, и высоту 65 мм; в основании цилиндра и конуса лежат круги диаметром 45 мм, а их высоты – по 65 мм.
Вычертите пирамиду, цилиндр, конус в трех прямоугольных проекциях. Построение пирамиды начинайте с горизонтальной проекции, как проекции, обеспечивающей однозначное определение формы тела. При построении вначале используйте сплошные тонкие линии, и обведите линии видимых контуров сплошными основными линиями, а линии невидимых контуров – штриховыми линиями.
Во всех заданиях проекции точек указаны видимыми. Необходимо достроить недостающие проекции точек.
Если точка видимая и лежит на поверхности, спроецированной в линию, то она указывается буквой без скобок.
Если точка невидимая, т.е. закрыта от глаз наблюдателя какой-либо поверхностью, то она указывается буквой, взятой в скобки. Например, А - видимая проекция точки; (А) – невидимая проекция точки.
При построении проекций точек, принадлежащих поверхности пирамиды и конуса, следует применять способ, дающий наибольшую точность - способ образующей.
Пример построения представлен на рисунке 91.
 Рисунок 90
Рисунок 90
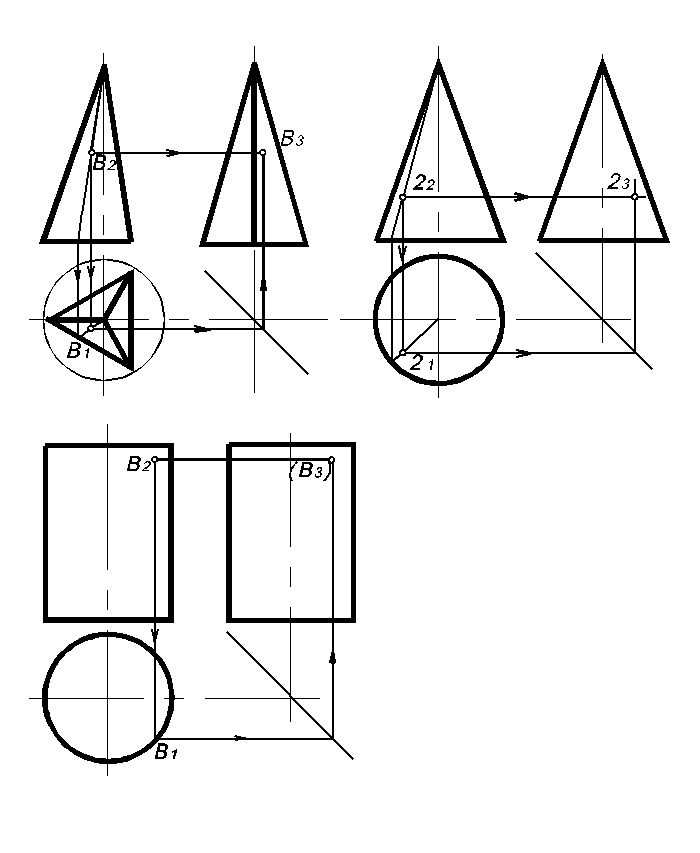
Рисунок 91
| № вар. | Xa | Ya | Za | Xb | Yb | Zb | Xc | Yc | Zc | Xd | Yd | Zd | Xe | Ye | Ze | Xk | Yk | Zk |
