Построение линии пересечения плоскостей общего положения
Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей.
Для нахождения таких точек используется методика по определению точки встречи прямой с плоскостью, только при этом в качестве плоскости выбирается одна из заданных плоскостей, а в качестве прямой – прямая, принадлежащая другой плоскости.
Рассмотрим, как это делается, на следующем примере (рис. 49).
Постановка задачи. Даны две плоскости общего положенияα, заданная треугольником ∆АВС и β – двумя параллельными прямыми m и n.
Построить прямую l пересечения плоскостей α и β: l=α∩β и определить видимость плоскостей, ограниченных ∆АВС и параллельными прямыми m и n.
Решение
1. Определяем первую точку М принадлежащею линии пересечения плоскостей l, как точку встречи прямой m с плоскость α: M⊂l; М=m∩α.
2. Определяем вторую точку N принадлежащею линии пересечения плоскостей l, как точку встречи прямой n с плоскость α: N⊂l; N=n∩α.
3. Через точки M и N проводим прямую пересечения плоскостей α и β: l=α∩β.

Рис. 49
4. Устанавливаем видимость плоскостей α и βотносительно друг друга. Для горизонтальной плоскости проекций с помощью горизонтально конкурирующих точек5 и 6 (точка 6 лежит на стороне АС треугольника, а точка 5 – на прямой т). Для фронтальной плоскости проекций с помощью фронтально конкурирующих точек1 и 7 (точка 1 лежит на стороне АС треугольника, а точка 7 – на прямой п). Направление взгляда при определении видимости проекций конкурирующих точек на эпюре показана символами (⇧) и (⇩).
3.6.Контрольные вопросы
1. Покажите на примерах, как строят точки и линии в плоскости общего положения.
2. Как строится линия пересечения плоскости общего положения проецирующей плоскостью?
3. Можно ли провести проецирующую плоскость через прямую общего положения?
4. Как определяются точки встречи прямой общего положения с плоскостью общего положения?
5. Как определяется видимость на эпюре прямой относительно плоскости?
6. Как определяются точки встречи проецирующей прямой с плоскостью общего положения?
7. Как определяются точки встречи прямой общего положения с плоскостью частного положения?
8. Покажите на примере построение прямой, параллельной плоскости общего положения.
9. Расскажите алгоритм построения перпендикуляра к плоскости, проходящего через заданную точку.
10. Сформулируйте, как построить на эпюре плоскость, перпендикулярную другой плоскости общего положения.
11. Сформулируйте, как построить на эпюре плоскость, параллельную другой плоскости.
12. Расскажите, как построить линию пересечения двух плоскостей общего положения.
13. Как определяется видимость при пересечении двух плоскостей общего положения?
Лекция 4. ПОВЕРХНОСТИ
4.1. Классификация поверхностей.
4.2. Задание поверхностей на эпюре Монжа.
4.3. Пересечение поверхности проецирующей плоскостью.
4.4. Пересечение прямой с поверхностью.
4.5. Пересечение многогранников
4.6. Пересечение многогранника с поверхностью второго рода.
4.7. Пересечение двух поверхностей второго порядка.
4.8. Контрольные вопросы.
Классификация поверхностей
Для того, чтобы ориентироваться во всем многообразии поверхностей, в способах задания и изображения поверхностей, необходимо классифицировать поверхности по общим, наиболее характерным признакам. Практически каждая поверхность может быть образована несколькими способами. Однако наиболее целесообразным способом образования поверхностей является кинематический, основанный на определенных законах движения. Такой подход к рассмотрению поверхностей позволяет выполнить их классификацию и, что не менее важно, выбрать наиболее рациональную технологию их воссоздания в металле или в другом материале.
Рассмотрим аппарат получения поверхностей (рис. 50).

Рис. 50
Введём обозначения:
– S – центр (точка относительно которой перемещается образующая);
– g – от слова genero (образую, порождаю);
– d – от слова dirigo (направляю).
Идея кинематического способа образования поверхностей состоит в том, что линия g,относительно центра S, в пространстве перемещается вдоль направляющей d и при движении образует поверхность. Линия может поступательно перемещаться, или вращается, или перемещается по винтовому закону, или, как по перилам, скользит по заданным линиям.
Линия g называется в этом случае образующей, а множество ее положений в пространстве образует кривую поверхность Ф.
Линии d, по которым скользит образующая g, называются направляющими. Значит, образующие g и направляющие d обязательно пересекаются друг с другом. Очевидно, от формы образующей и характера её изменения зависит класс поверхности.
Если образующая g – прямая линия, то поверхность Ф называется линейчатой.
Если образующая g – кривая линия, то поверхность называется нелинейчатой.
Таким образом, выделено два класса поверхностей – линейчатые и нелинейчатые.
Из наиболее часто встречающихся в технике поверхностей выделены поверхности вращения.
Поверхностью вращения называется поверхность, образованная вращением образующей g вокруг оси вращения.
На рис. 51 изображены линейчатая поверхность вращения (конус), нелинейчатая поверхность вращения (глобоид) и многогранник (пирамида).

Рис. 51
При вращении образующей, каждая ееточка описывает окружность с центром S на оси вращения. Эти окружности называются параллелями. Параллель с минимальным размером радиуса называется горлом, а с максимальным размером радиуса – экватором.
Кривые, получающиеся в сечении тела вращения плоскостями, проходящими через ось, называются меридианами. Меридиан, параллельный фронтальной плоскости проекций, называется главным.
При вращении кривой 2-го порядка вокруг её оси образуется поверхность 2-го порядка:
· окружность вокруг диаметра – сфера,
· эллипс вокруг малой оси – сжатый эллипсоид вращения,
· эллипс вокруг большой оси – вытянутый эллипсоид вращения,
· парабола вокруг оси – параболоид вращения,
· гипербола вокруг мнимой оси – однополостный гиперболоид вращения,
· гипербола вокруг действительной оси – двуполостный гиперболоид вращения.
Если вращать вокруг оси прямолинейную образующую (прямую), то возможны 3 вида поверхностей:
· если g пересекает ось вращения – коническая поверхность вращения,
· если g параллельна оси вращения – цилиндрическая поверхность вращения,
· если g скрещивается с осью вращения – однополостный гиперболоид вращения.
Задание поверхностей на эпюре Монжа
На эпюре многогранники изображаются проекциями своей сетки – рис. 52. Совокупность ребер и вершин многогранника называется его сеткой. Каждая вершина имеет своё обозначение. Ребра многогранников есть линии пересечения смежных граней. Каждая грань – это часть плоскости, ограниченной ребрами и сторонами основания многогранника.
Рассмотрим, в каком случае точка пространства будет принадлежать многограннику.
Понятно, что точка пространства может принадлежать: вершине многогранника, его ребру или грани многогранника.
В первом и втором варианте проблем изображения точки на чертеже многограннике нет.
Если же точка принадлежит грани многогранника, т.е. плоскости, надо пользоваться информацией: точка лежит в плоскости, если она лежит на прямой этой плоскости.
Условимся записывать обозначение точки, лежащей на невидимой для наблюдателя грани, в скобках, например, (E2).
На рис. 52а задана проекция (E2), т.е. точка E располагается грани ADS четырёхгранной пирамиды, невидимой относительно фронтальной плоскости проекции. Для нахождения горизонтальной проекции проводится прямая S-1 в грани BCS через вершину S, на горизонтальной проекции которой и лежит E1.

Рис. 52
На рис. 52б задана проекция F2, т.е. точка F располагается на грани BCS правильной четырёхгранной пирамиды, видимой относительно фронтальной плоскости проекции. Для нахождения горизонтальной проекции проводится в грани BCS прямая, параллельная стороне AD основанияпирамиды. На горизонтальной проекции этой прямой и лежит F1.
На рис. 52в задана проекция (G2), т.е. точка G располагается на грани 1-2-BA наклонной призмы, видимой относительно фронтальной плоскости проекции. Для нахождения горизонтальной проекции проведена в грани 1-2-BA прямая, параллельная ребрам призмы. На горизонтальной проекции этой прямой и лежит G1.
У прямой призмы (рис. 52г) грани занимают горизонтально-проецирующее положение, поэтому горизонтальные проекции K1 и L1 определяются с помощью вертикальных линий связи на следах граней.
Поверхности вращения на эпюре задается их очерками. Очерк поверхности – это линия, разграничивающая проекцию фигуры от остального пространства чертежа. Для построения очерка необходимо построить крайние граничные очерковые образующие. Очерковые образующие лежат в плоскости, параллельной плоскости проекций.
На рис. 53 приведены примеры изображения некоторых тал вращения на эпюре Монжа: прямой круговой конус (рис. 53а); наклонный круговой конус (рис. 53б); прямой круговой цилиндр (рис.53в); наклонный круговой цилиндр (рис. 53г).

Рис. 53
Если очерки для тела вращения (кроме сферы) называются в зависимости от плоскости проекций на которую оно спроецировано (горизонтальная, фронтальная и профильная), то для сферы (рис. 54) эти очерки носят специфические названия (по аналогии с глобусом):
– очерк на π2 – главный (нулевой) меридиан;
– очерк на π1 – экватор;
– очерк на π3 – профильный меридиан.

Рис. 54
Для построения точек на поверхностях используются образующие, проходящие через эти точки.
На рис. 53а задана проекция точки (А2), т.е. точка А располагается на невидимой стороне прямого кругового конуса относительно фронтальной плоскости проекций. Для нахождения горизонтальной проекции проводится образующая S-1, на горизонтальной проекции которой и лежит А1.
На рис. 53б задана проекция В1 точки В, лежащей на видимой стороне наклонного кругового конуса относительно горизонтальной плоскости проекций. Для нахождения фронтальной проекции проводится образующая S-2, на фронтальной проекции которой и лежит В2.
У прямого кругового цилиндра (рис. 53в) боковая поверхность занимает горизонтально-проецирующее положение, поэтому горизонтальные проекции С1 и D1 определяются с помощью вертикальных линий связи на следе боковой поверхности.
На рис. 53г заданы проекции Е2 и (F2) точек Е и F расположенных соответственно на видимой и невидимой сторонах наклонного цилиндра относительно фронтальной плоскости проекций. Для нахождения горизонтальных проекций проводятся образующие, параллельные очерковым боковой поверхности на которых находятся горизонтальные проекции этих точек Е1 и F1.
Для нахождения точек на поверхности сферы (рис. 55) используют дополнительные широты и удаления от оси вращения.
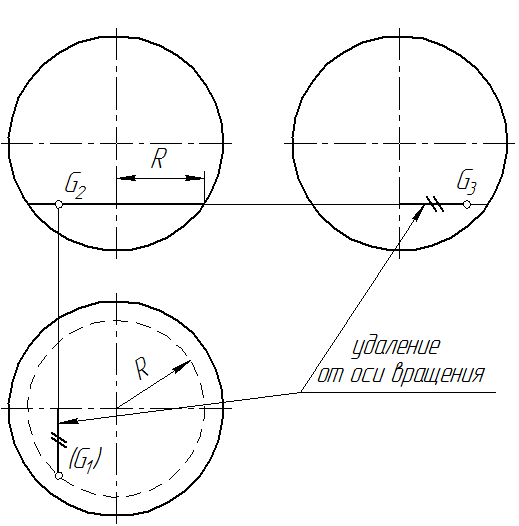
Рис. 55
На рис. 55 задана проекция G2 точки G, лежащей ниже экватора на видимой стороне сферы относительно фронтальной плоскости проекций. Для нахождения горизонтальной проекции: вначале строится дополнительная широта, проходящая через заданную точку, а затем по инварианту принадлежности определяется горизонтальная проекция точки (G1).
Следует отметить, что проекция точки на горизонтальной плоскости проекций не видима, т.к. точка G располагается ниже экватора.
Профильная проекция точки G3 определяется по горизонтальной линии связи и удалению от оси вращения (см. рис. 55). Проекция G3 видима потому, что фронтальная проекция точки G2 находится правей фронтальной проекции профильного меридиана.
