Алгоритм Сазерленда-Ходжмена
В этом алгоритме исходный и каждый из промежуточных многоугольников последовательно отсекается относительно одной прямой отсекающего окна (рис. 7.2).
Результатом работы алгоритма является список вершин многоугольника, у которого все вершины лежат по видимую сторону окна отсечения. Так как каждая сторона многоугольника отсекается независимо от других, то достаточно рассмотреть только возможные ситуации расположения одного отрезка относительно одной отсекающей плоскости (рис. 7.3).
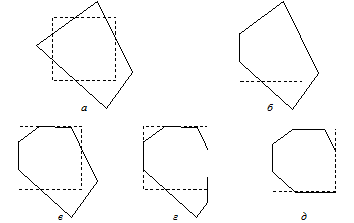
Рис. 7.2. Последовательное отсечение многоугольника
по алгоритму Сазерленда-Ходжмена

Рис. 7.3. Варианты расположения отрезков:
а – полная видимость; б – полная невидимость;
в – выход из области видимости; г – вход в область видимости
Для первой вершины многоугольника необходимо определить только факт ее видимости. Если она видима, то она попадает в результат и становится начальной точкой (обозначим ее буквой S), если она не видима, то она также становится начальной точкой S, но в результат не заносится. Далее, будем рассматривать каждую точку P из списка вершин многоугольника как конечную точку ребра, начальной точкой S которого является вершина, предшествующая P. Тогда возможны только четыре ситуации взаимного расположения ребра и отсекающей плоскости:
– полная видимость (рис. 7.3,а) – в результат заносятся координаты вершины P и она становится начальной точкой S;
– полная невидимость (рис. 7.3,б) – в результат ничего не заносится, но точка P становится начальной точкой S;
– выход из области видимости (рис. 7.3,в) – в результат заносятся координаты точки пересечения I, точка P становится начальной точкой S;
– вход в область видимости (рис. 7.3,г) – в результат заносятся координаты точки пересечения I и координаты вершины P, точка P становится начальной точкой S.
При реализации алгоритма необходимо, чтобы отсекаемый и отсекающий многоугольники были выпуклыми. Для определения факта выпуклости многоугольника применяются алгоритмы, описанные в предыдущей главе, но для определения видимости точки относительно отсекающей плоскости приведем еще один алгоритм (в алгоритме Кируса-Бека – умножение на нормаль, этот алгоритм пригоден и в данном случае).
Определение видимости точки эквивалентно определению той стороны границы отсекающей плоскости, по которую лежит эта точка. Если ребра отсекающего многоугольника обходятся по часовой стрелке, то его "внутренность" лежит по правую сторону от границы, иначе – по левую, т.е. необходимо определить, справа или слева находится точка. Для этого применяется следующий алгоритм: пусть две точки P1 и P2 лежат на отсекающей плоскости, P3 – тестовая (пробная) точка. Эти три точки задают плоскость, на которой лежат два вектора P1P2 и P1P3. Если эту плоскость считать плоскостью XY, то у векторного произведения P1P3 Ä P1P2 ненулевой будет только компонента Z, равная: (X3 – X1) * (Y2 – Y1) – (Y3 – Y1) * (X2 – X1), если знак этой компоненты будет положительным, нулевым или отрицательным, то точка P3 будет лежать соответственно справа, на или слева от прямой P1P2.
Приведем пример (рис. 7.4). Координаты точки P1 = (–1,0), координаты точки P2 = (–1,2). Отсекающая плоскость X = –1. Необходимо определить положение двух тестовых точек P3 (–2,1) и P'3 (2,1).
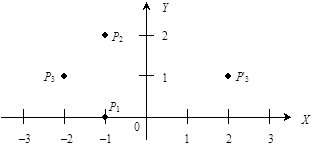
Рис. 7.4. Определение видимости точки относительно
отсекающей плоскости
Для точки P3:
(X3 – X1) * (Y2 – Y1) – (Y3 – Y1) * (X2 – X1) =
= ((–2) – (–1)) * (2 – 0) – (1 – 0) * ((–1) – (–1)) = –2
и, следовательно, точка P3 находится слева от плоскости X = –1. Для тестовой точки P'3 значение этого выражения равно 6, следовательно, точка P'3 находится справа от плоскости X = –1.
При дальнейшем развитии алгоритма его авторы (Сазерленд и Ходжмен) показали, как избежать порождения и запоминания вершин промежуточных многоугольников. Для этого вместо отсечения каждого ребра многоугольника одной плоскостью, ограничивающей окно, необходимо отсекать каждое ребро последовательно всеми границами окна. Это делает данный алгоритм более пригодным для аппаратной реализации. Кроме того, этот алгоритм можно распространить и на трехмерные области.
