Двумерный алгоритм Коэна-Сазерленда

Вся область экрана делится на 9 частей (рис. 6.1). Для определения, к какой из девяти областей принадлежит конец отрезка, вводится 4-битовый код; биты считаются справа и единица ставится в бит, если:

– 1 бит – точка левее окна;

– 2 бит – точка правее окна;

– 3 бит – точка ниже окна;

– 4 бит – точка выше окна.

Центральная область имеет код – 0000.

Рис. 6.1. Задание кодов областей для алгоритма

Коэна-Сазерленда

Отсюда алгоритм: если коды обоих концов отрезка равны 0000, то отрезок полностью видим (и мы изображаем его), если побитовое логическое произведение кодов концов отрезка не равно нулю, то отрезок полностью невидим (и мы отбрасываем его), иначе – отрезок или виден частично, или целиком невидим. В последнем случае ищется пересечение отрезка со сторонами окна либо параметрическим способом, либо методом разбиения средней точкой.

Двумерный FC-алгоритм

В данном алгоритме кодируется весь отрезок целиком. Схема кодирования близка к используемой в алгоритме Коэна-Сазерленда. Все пространство экрана разбивается на 9 частей и они кодируются цифрами от 1 до 9 (рис. 6.2). Отрезок кодируется следующим образом:

LineCode(V₀V₁) = Code(V₀)*16 + Code(V₁),

где Code(V₁) – код конечной точки;

Code(V₀) – код начальной точки,

*16 – означает сдвиг влево на 4 разряда,

LineCode(V₀V₁) – код отрезка.

Рис. 6.2. Задние кодов областей

для FC-алгоритма

Так как каждый код может принимать только девять значений, то имеется 81 возможный вариант расположения отрезка и требуется свой набор вычислений для определения отсечения отрезка за минимальное время. Однако имеется всего 8 основных случаев отсечения, остальные симметричны им. Иллюстрации для случаев 1-7 приведены на рис. 6.3, а для случая 8 – на рис. 6.4.

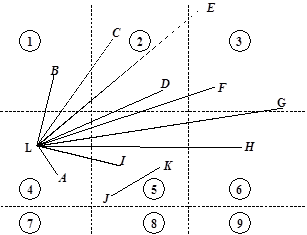
Рис. 6.3. Варианты расположения отрезка для неугловых

областей (FC-алгоритм)

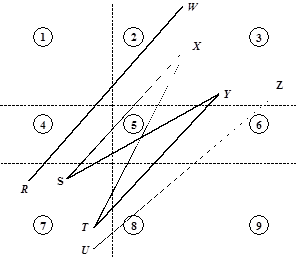
Рис. 6.4. Варианты расположения отрезка для угловых

областей (FC-алгоритм)

Итак:

Случай 1 – начальная и конечная точки отрезка находятся в области 4 (отрезок LA, LineCode(V₀V₁) = 44). Отрезок не пересекает видимую область и отбрасывается.

Случай 2 – начальная точка находится в области 4, конеч-
ная – в области 1 (отрезок LB, LineCode(V₀V₁) = 41). Отрезок не пересекает видимую область и отбрасывается.

Случай 3 – начальная точка находится в области 4, конеч-
ная – в области 2 (отрезки LC и LD, LineCode(V₀V₁) = 42). Отрезок явно пересекает X_лев. Вычисляем точку пересечения отрезка с левым ребром – (X_лев, Y_п). Eсли Y_п > Y_верхн, то это отрезок LC, он не пересекает видимую область и отбрасывается. Иначе, это отрезок LD, пересекающий видимую область и необходимо вычислить точку пересечения отрезка с Y_верхн и изобразить видимую часть отрезка.

Случай 4 – начальная точка находится в области 4, конеч-
ная – в области 3 (отрезки LE, LF и LG, LineCode(V₀V₁) = 43). Вычисляем точку пересечения с левым ребром – (X_лев, Y_п1). Eсли Y_п1 > Y_верхн, то это отрезок LE, он не пересекает видимую область и отбрасывается, иначе это отрезки LF или LG. Вычисляем точку пересечения с правым ребром (X_прав, Y_п2). Eсли Y_п2 > Y_верхн, то это отрезок LF и необходимо вычислить точку пересечения с верхним ребром и изобразить видимую часть отрезка. Иначе это отрезок LG, точки пересечения с левым и правым ребрами известны, следовательно, изображаем видимую часть отрезка.

Случай 5 – начальная точка находится в области 4, конеч-
ная – в области 6 (отрезок LH, LineCode(V₀V₁) = 46). Вычисляем точки пересечения с левым и правым ребрами и изображаем видимую часть отрезка.

Случай 6 – начальная точка находится в области 4, конеч-
ная – в области 5 (отрезок LI, LineCode(V₀V₁) = 45). Вычисляем точку пересечения с левым ребром и изображаем видимую часть отрезка.

Случай 7 – начальная точка находится в области 5, конеч-
ная – в области 5 (отрезок JK, LineCode(V₀V₁) = 55). Отрезок полностью видим, изображаем его.

Случай 8 – начальная точка находится в области 7, конеч-
ная – в области 3 (отрезки RW, SX, SY, TX,TY,UZ LineCode(V₀V₁) = 73). Вычисляем точку пересечения с левым ребром – (X_лев, Y_п1). Eсли Y_п1 > Y_верхн, то это отрезок RW, он не пересекает видимую область и отбрасывается. Вычисляем точку пересечения с правым ребром – (X_прав, Y_п2). Eсли Y_п2 < Y_нижн, то это отрезок UZ, он не пересекает видимую область и отбрасывается. Если Y_п1 > Y_нижн, то начальная точка S и если Y_п2 < Y_вехн, то это отрезок SY, и мы изображаем его видимую часть, иначе – это отрезок SX, вычисляем точку пересечения с верхней стороной и также изображаем видимую часть отрезка. Оставшийся вариант – начальная точка T и если Y_п2 < Y_вехн, то это отрезок TY и мы изображаем его видимую часть, иначе – это отрезок TX, вычисляем точку пересечения с верхней стороной и также изображаем видимую часть отрезка.

Алгоритм Кируса-Бека

Алгоритм Кируса-Бека относится к классу алгоритмов с параметрическим представлением отрезка и окна отсечения. При создании надежного алгоритма отсечения необходимо иметь хороший метод определения местоположения относительно окна точки, принадлежащей отрезку, – внутри, на границе или вне окна. Для этого в алгоритме Кируса-Бека используется вектор нормали.

Возьмем выпуклую двумерную область R (рис. 6.5) – она должна быть выпуклым многоугольником. Внутренняя нормаль в точке a, лежащей на границе R, удовлетворяет условию:

n_вн * (b– a) ³ 0,

где b – любая точка, лежащая на границе R.

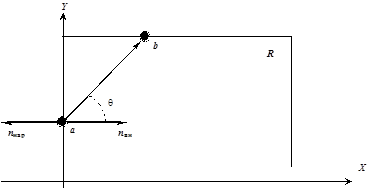
Рис. 6.5. Определение местоположения точки относительно
окна отсечения в алгоритме Кируса-Бека

Скалярное произведение двух векторов равно:

V₁ * V₂ = çV₁ç ×çV₂ç×cos(Q),

где Q – меньший из двух углов, образованных V₁ и V₂. Причем, если Q = p/2, то V₁ ×V₂ = 0 и вектора V₁и V₂ перпендикулярны. Угол Q между n_вн и любым вектором между точками a и b всегда принадлежит интервалу – p/2 £ Q£ p/2 и, следовательно, cos(Q) всегда ³ 0 и скалярное произведение n_вн * (b – a) неотрицатель-
но (для внешней (наружной) нормали скалярное произведение n_нар * (b – a) всегда неположительно).

Параметрическое представление отрезка имеет вид:

P(t) = P₁ + (P₂ – P₁) ×t; 0 £ t £ 1.

Если f – граничная точка выпуклой области R, а n – внутренняя нормаль к одной из ограничивающих эту область плоскостей, то для любой конкретной величины t (т.е. для любой точки отрезка P₁P₂) из условия n * (P(t) – f) < 0 следует, что вектор (P(t) – f)

направлен вовне области R, из условия n *(P(t) – f) = 0 следует, что вектор (P(t) – f) принадлежит плоскости, которая проходит через f, и перпендикулярен нормали, из условия n * (P(t) – f) > 0 следует, что вектор (P(t) – f) направлен внутрь области R (рис. 6.6).

Из всех, условий взятых вместе, следует, что бесконечная прямая пересекает замкнутую область (выпуклую двумерную) ровно в двух точках и уравнение n *(P(t) – f) = 0 имеет только одно решение и точка P(t) будет точкой пересечения отрезка с граничной плоскостью.

Из всего вышесказанного и вытекает алгоритм Кируса-Бека.

Параметрическое описание отрезка (как уже отмечалось выше) имеет вид:

P(t) = P₁ + (P₂ – P₁) ×t; 0 £ t £ 1.

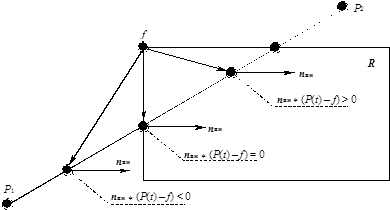
Рис. 6.6. Исходные данные для алгоритма Кируса-Бека

Скалярное произведение внутренней нормали на вектор, начинающийся в произвольной точке отрезка и заканчивающийся в другой точке, лежащей на той же границе окна (n_i * (P(t) – f_i );
i = 1,2…), будет положительным, равным нулю или отрицательным в зависимости от того, будет ли избранная точка отрезка лежать с внутренней стороны границы, на самой границе или с ее внешней стороны. Это справедливо для любого ребра. Подставим P(t) для нахождения пересечения:

n_i * [P₁ + (P₂ – P₁) ×t – f_i] = 0.

Или в другой форме:

n_i * [P₁ –f_i] +n_i * [P₂ – P₁] × t = 0.

Вектор (P₂ – P₁) – определяет ориентацию отрезка, а вектор (P₁ – f_i) пропорционален расстоянию от первого конца отрезка до избранной граничной точки. Обозначим D = (P₂ – P₁) – директриса или ориентация отрезка, а w_i = (P₁ – f_i) – весовой множитель, тогда:

t ×(n_i *D) + w_{i *} n_i = 0,

t = –(w_i *n_i) / (n_i *D); D ¹ 0; i = 1, 2, 3, …

Равенство D нулю означает, что P₂ = P₁, т.е. вырождение отрезка в точку и при этом, если w_i *n_i < 0, то точка вне окна отсечения, если w_i *n_i = 0, то точка находится на границе окна отсечения, если w_i *n_i > 0, то точка внутри окна отсечения. Вычисляем t, если значение лежит за пределами интервала 0 £ t £ 1, то можно его проигнорировать. Может получиться более двух значений t в допустимом интервале. Эти значения следует разбить на две группы: нижнюю и верхнюю в зависимости от того, к началу или концу отрезка будет ближе вычисленная точка. Необходимо найти наибольшую из нижней группы и наименьшую из верхней группы. При этом, если n_i *D > 0, то найденное значение t рассматривается в качестве возможного нижнего предела, иначе – верхнего. Блок-схема алгоритма приведена на рис. 6.7.

Для успешной реализации алгоритма Кируса-Бека необходимо знать, выпуклый многоугольник или нет, и определить уравнение внутренней нормали.