Определение натуральной величины отрезка прямой способом прямоугольного треугольника.

Пусть требуется определить расстояние между двумя точками А и В, заданными своими проекциями.

Пусть дан отрезок прямой в пространстве (рис. 73). А₁В₁ – его горизонтальная проекция. Проведем через точку А прямую, параллельную А₁В₁, и отметим точку В’. В прямоугольном треугольнике АВ’В катет АВ’ равен горизонтальной проекции А₁В₁ отрезка АВ, катет ВВ’ равен разности концов расстояний точек В и А до П₁, α – угол, который образует прямая АВ с горизонтальной плоскостью проекций. Таким образом, чтобы на комплексном чертеже (рис. 73, а) найти истинную величину отрезка АВ, мы должны при катете А₁В₁ построить прямоугольный треугольник, равный треугольнику АВ’В. Для этого в точке В₁ восстанавливаем перпендикуляр к А₁В₁ и на нем откладываем отрезок В₁В₀, равный разности расстояний концов отрезка АВ до П₁, т.е. отрезок Δh. Гипотенуза А₁В₀ прямоугольного треугольника А₁В₁В₀ есть искомая величина. Если аналогичные построения выполнить на фронтальной проекции А₂В₂, то в качестве второго катета следует взять разность глубин.

Итак, натуральная величина отрезка прямой равна гипотенузе прямоугольного треугольника, у которого один катет равен проекции отрезка, а второй катет – соответственно разности высот или глубин.

Рис. 73 Рис. 73 а

Перпендикулярность двух прямых, прямой и плоскости.

Решение многих метрических задач связано с проведением перпендикулярных прямых и плоскостей и основывается на следующей теореме.

Теорема. Если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то прямой угол на эту плоскость проекций проецируется в виде прямого же угла (рис. 74).

Рис. 74

Дано: ; .

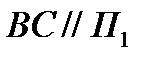Требуется доказать: 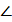А₁В₁С₁ = 90⁰.

Доказательство:

ВС АВ по условию, ВС ВВ₁ по построению (т.к. ВС 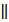П₁, а ВВ₁ П₁). Следовательно ВС плоскости Γ (АВ ∩ ВС).

ВС 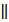В₁С₁, поэтому В₁С₁ Γ.

Следовательно, В₁С₁ будет перпендикулярна прямой А₁В₁ = Γ П₁, т.е. 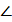А₁В₁С₁ = 90⁰.

Из доказанной теоремы вытекает следствие: если прямая n перпендикулярна плоскости Δ = h f, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости (n₁ h₁), а фронтальная проекция n₂ перпендикулярна фронтальной проекции f₂ фронтали этой плоскости. В самом деле, так как h 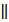П₁, а f 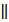П₂, то на основании предыдущей теоремы n₁ будет перпендикулярна h₁, а n₂ будет перпендикулярна f₂ (рис. 75).

Рис. 75

Задача. Найти расстояние от точки D до плоскости ΔАВС.

Решение задачи состоит из трех этапов:

1. На основании предыдущего следствия из точки D (D₁, D₂) проводим перпендикуляр n: n₁ h₁ и n₂ f₂ (рис. 76).

2. Строим точку К пересечения этого перпендикуляра с плоскостью АВС (первая основная позиционная задача).

3. Находим натуральную величину отрезка DK (D₁К₁, D₂К₂) способом прямоугольного треугольника.

Рис. 76

Развертки поверхностей.

Разверткой поверхности Ф называется плоская фигура Ф’, все точки которой находятся во взаимно однозначном соответствии с точками поверхности и удовлетворяющая следующим свойствам:

1) Длина некоторой линии на поверхности Ф равна длине соответствующей ей линии на развертке Ф’;

2) Угол α между двумя линиями на поверхности равен углу α’ между соответствующими им линиями на развертке;

3) Площадь некоторой замкнутой фигуры на поверхности равна площади соответствующей ей фигуре на развертке.

Поверхности, удовлетворяющие этим трем свойствам, называются развертывающими. К развертывающимся поверхностям относятся многогранные, конические, цилиндрические и торсовые поверхности.

Развертки многогранников.

Разверткой многогранника будет плоская фигура, получаемая последовательным совмещением всех граней многогранника в одну плоскость. Таким образом, построение развертки многогранника сводится к нахождению натуральных величин его граней – плоских многоугольников, что, в свою очередь, сводится к определению натуральных величин его ребер.

Пример: построить развертку треугольной пирамиды SABC, заданной ее комплексным чертежом (рис. 77).

Рис. 77

Рассмотрим грань SAB. Так как S₁A₁ || OX, то S₂A₂ равна натуральной величине. Отрезок А₁В₁ есть истинная величина стороны АВ треугольника SАВ. Способом вращения найдем истинную величину ребра SВ. Итак, в треугольнике SАВ имеем:

|SA| = |S₂A₂|, |AB| = |A₁B₁|, |SB |= |S_{2 2}|.

По трем сторонам строим SAB. Пристраиваем к нему к стороне SB следующий SBC, найдя предварительно истинную величину ребра SC и т. д. Достроив основание пирамиды АВС, получим полную развертку пирамиды SABC (рис. 78). Точки, расположенные внутри контура развертки, находятся во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки (например, точки N и N₀).

Рис. 78