Четыре основные задачи, решаемые заменой плоскостей
Проекций
Задача 1.Прямую общего положения преобразовать в прямую уровня (параллельную плоскости проекций).
Алгоритм преобразования (рис.4.5):
1) П4||a или П5||a
2) ^ - проецирование ортогонально новой плоскости проекций;
3) r - const - сохранение расстояний.
Т.к. а||П4 или ||П5 , то длина отрезка АВ может быть найдена по чертежу:
|АВ|=|А4В4|=|А5В5|
a - угол наклона прямой а к горизонтальной пл.пр.
b - угол наклона прямой а к фронтальной пл. пр.
| На прямой общего положения а задаем отрезок АВ |АВ| Ì а |  | |
| 1 вариант П2ÞП4^П1 П4 || а х14 || а1 | 2 вариант П1ÞП5^П2 П5 || а х25 || а2 | |
Рисунок 4.5
Задача 2.Прямую уровня сделать проецирующей прямой (рис. 4.6 и 4.7) .
| горизонталь h | фронталь f |
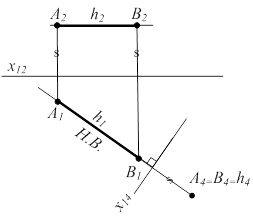 |  |
| П2 Þ П4 ^ П1 П4 ^ h x14 ^ h1 | П1 Þ П5 ^ П2 П5 ^ f x25 ^ f2 |
| Рисунок 4.6 | Рисунок 4.7 |
Алгоритм преобразования (рис.4.6):
1) П4 ^ h;
2) ^ - проецирование ортогональное;
3)r - const .
Задача 3. Плоскость общего положения сделать проецирующей плоскостью в новой системе проекций (рис. 4.8).
Для решения этой задачи новую плоскость проекций нужно расположить перпендикулярно данной плоскости общего положения и перпендикулярно одной из плоскостей проекций. Это возможно, если направление проецирования совпадает с направлением соответствующих линий уровня пл. общего положения. Тогда все линии уровня изобразятся точками на новой плоскости проекций и дадут вырожденную в прямую проекцию плоскости.
S(АВС) - общего положения П2 Þ П4 ^ П1  П4 ^ S h Ì S (h É A) П4 ^ h x14 ^ h1 П4 ^ S h Ì S (h É A) П4 ^ h x14 ^ h1 | 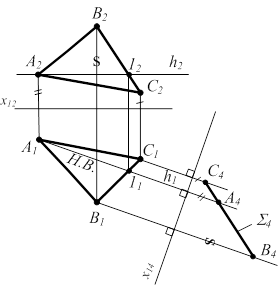 |
Рисунок 4.8
П4^S(^h1)
1) П2 ® П4 ^ S
2) ^ - проецирование ортогональное;
3) r - const .
Если плоскость проходит через перпендикуляр к другой плоскости, то она перпендикулярна ей. Т.е., если x14^h1, то S^П4 или плоскость вырождается в прямую S4 .
Задача 4. Ввести новую плоскость проекций так, чтобы проецирующая плоскость стала бы плоскостью уровня в новой системе проекций (параллельна новой плоскости проекций) (рис. 4.9).
Решение этой задачи позволяет определить величины плоских фигур.
Новую плоскость проекций нужно расположить параллельно заданной плоскости.
S(АВС)^П1 ; П2 Þ П4^П1 Т.е. преобразование только такое:  П2 Þ П4 ^П1 , и одновременно П4 || S Þ х14 || S1 Следовательно: DАВС = DА4В4С4 П2 Þ П4 ^П1 , и одновременно П4 || S Þ х14 || S1 Следовательно: DАВС = DА4В4С4 | 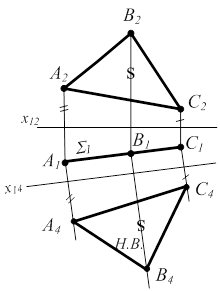 |
Рисунок 4.9
Алгоритм преобразования:
1) П4 ... || S
2) ^ - проецирование ортогонально новой плоскости;
3) r - const - сохранение расстояний.
Если выполнить 1 и 2 задачи друг за другом на одном чертеже, прямая общего положения может преобразоваться в проецирующую прямую.
Последовательное решение 3 и 4 задач на одном чертеже позволяет плоскость общего положения преобразовать в плоскость уровня.
Вопросы для самоконтроля:
1) В чем суть способа замены плоскостей проекций?
2) Приведите четыре основных алгоритмов замены плоскостей проекций.
3) Выполнить 1 и 2 задачи друг за другом, чтобы отрезок АВ прямой общего положения с рисунка 2.1 преобразовать в проецирующую прямую.
4) Последовательным решением 3 и 4 задач плоскость D(АВС) общего положения с рисунка 2.5 преобразовать в плоскость уровня.
Метрические задачи
Метрические задачи можно разделить на три группы.
1 группа задач: определение расстояний от точки до другой точки, прямой, плоскости или поверхности; от прямой до другой прямой или плоскости; от плоскости до плоскости.
2 группа задач: определение углов между пересекающимися или скрещивающимися прямыми; между прямой и плоскостью; между плоскостями (двугранные углы).
3 группа задач: определение величины плоской фигуры или части поверхности (развертка, сечение).
Эти задачи решаются значительно проще, если геометрические элементы занимают частное положение относительно плоскостей проекций. Поэтому при решении метрических задач используются способы преобразования комплексного чертежа.
Рассмотрим решения метрических задач.
Задача 1. Расстояние от точки до точки (длина отрезка).
Рассмотрим три способа построения натуральной величины отрезка для решения метрических задач 1 группы.
а) С помощью построения прямоугольного треугольника(рис. 5.1):
ÐA1B1B′1 = 90°  |B1B′1| = |B2 B12| - |A2A12| |АВ| = |А1В′1| |B1B′1| = |B2 B12| - |A2A12| |АВ| = |А1В′1| |  |
Рисунок 5.1
б) Вращением отрезка вокруг проецирующей прямой(рис. 5.2):
i Î A i ^ П1 - ось вращения А1В1 = R – радиус вращения т.В  А′1В′ 1|| x12 |АВ|=|А2В′2| А′1В′ 1|| x12 |АВ|=|А2В′2| | 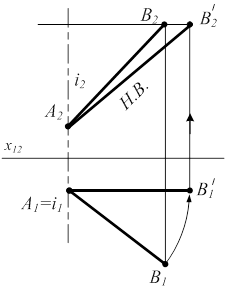 |
Рисунок 5.2
в) Заменой плоскостей проекций(рис. 5.3):
 |АВ| = |А4В4| |АВ| = |А4В4| |  |
Рисунок 5.3
Задача 2. Расстояние от точки до прямой измеряется отрезком перпендикуляра, проведенного из точки к прямой. Отрезок этого перпендикуляра виден в натуральную величину в том случае, если он проведен к проецирующей прямой (рис. 5.4).
| 1) П2 Þ П4 || AB Þ x14 || A1B1 2) П1 Þ П5 ^ AB Þ x45 ^ A4B4 3) |К505| = |К0| - искомое расстояние (К404 || x45 , т.к. в этой системе проекций найденное расстояние является прямой уровня или горизонталью) | 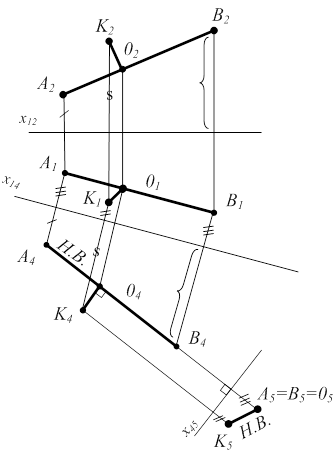 |
Рисунок 5.4
Задача 3. Расстояние от точки до плоскости измеряется отрезком перпендикуляра, опущенного из точки на плоскость. Отрезок этого перпендикуляра виден в натуральную величину, если плоскость занимает проецирующее положение, т.е. вырождается в прямую (рис. 5.5).
| 1) h Î å(ABC) 2) П2 Þ П4^h ; x14^h1 3) |К404|=|К0| - искомое расстояние (К101 || x14 ; 02012 =04014) | 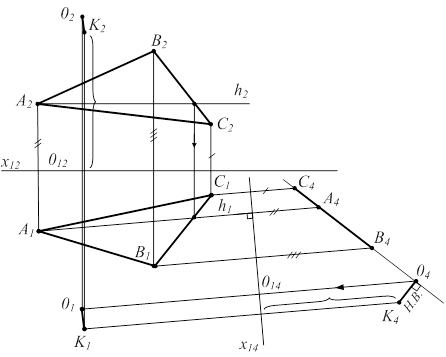 |
Рисунок 5.5
Задача 4. Расстояние между параллельными прямыми измеряется отрезком перпендикуляра между ними. Этот отрезок виден в натуральную величину, если прямые проецирующие, т.е. вырождаются в точку (рис. 5.6) .
| 1) П2 Þ П4 || a ; b или x14 || a1 ; b1 2) П1 Þ П5 ^a ; b или x45 ^a4 ; b4 3) |К505 |= |К0| - искомое расстояние (К404 || x45 ; К4 - произвольное положение на прямой а) |   |
Рисунок 5.6
Задача 5. Расстояние между скрещивающимися прямыми измеряется отрезком перпендикуляра, когда одна из прямых занимает проецирующее положение, т.е. вырождается в точку (a5 на рис.5.7)
а и b - скрещивающиеся прямые общего положения  1) П2 Þ П4 || a или x14 || a1 2) П1 Þ П5 ^a или x45 ^a4 3) |К505 | = |К0| - искомое расстояние К505 ^b5 К404 || x45 1) П2 Þ П4 || a или x14 || a1 2) П1 Þ П5 ^a или x45 ^a4 3) |К505 | = |К0| - искомое расстояние К505 ^b5 К404 || x45 | 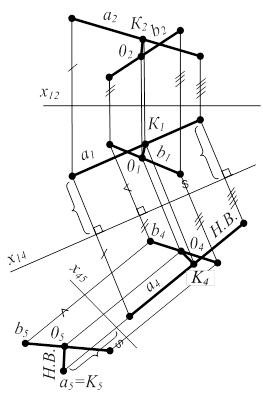 |
Рисунок 5.7
Задача 6. Расстояние от прямой до параллельной ей плоскости измеряется отрезком перпендикуляра, опущенного из любой точки прямой на плоскость. Эти отрезки перпендикуляров видны в натуральную величину, когда плоскость занимает проецирующее положение, т.е. вырождается в прямую. Взять на заданной прямой любую точку и решение задачи сводится к определению расстояния от точки до плоскости.
Для определения параллельности прямой и плоскости на комплексном чертеже используется признак параллельности: прямая параллельна плоскости, если в плоскости есть прямая, параллельная данной.
Задача 7. Расстояние между параллельными плоскостямиизмеряется отрезком перпендикуляра между ними. Этот отрезок виден в натуральную величину, если плоскости занимают проецирующее положение, т.е. вырождаются в прямые (т.е. в свои следы).
Для определения параллельности двух плоскостей на комплексном чертеже используется известный признак параллельности плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.
Расстояние между параллельными плоскостями общего положения определяется заменой плоскостей проекций (решением 3 задачи способа): пл. П2 заменяется на пл. П4 перпендикулярную параллельным плоскостям. Новая ось чертежа располагается перпендикулярно горизонтальным проекциям горизонталей заданных плоскостей. Искомое расстояние определяется отрезком между следами плоскостей на новой плоскости проекций.
Задача 8. Истинная величина плоских углов определяется методом замены плоскостей проекций, для чего плоскость угла преобразуется в плоскость уровня. Последовательно решаются 3 и 4 основные задачи замены плоскостей проекций.
Задача 9. Величина угла между скрещивающимися прямыми определяется, как угол между двумя пересекающимися прямыми, параллельными данным прямым.
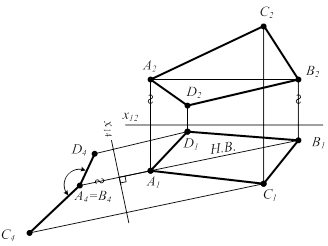
Задача 10. Величина двугранного угла определяется, как угол между двумя проецирующими плоскостями, когда линия пересечения плоскостей - ребро двугранного угла занимает проецирующее положение, т.е. вырождается в точку (рис.5.8а).
 | 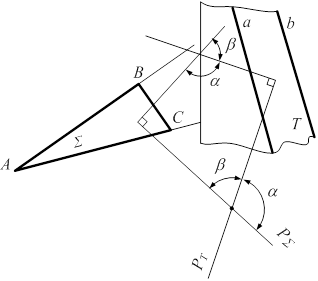 |
| а) | б) |
Рисунок 5.8
Если ребро не задано, то определяется угол между перпендикулярами, проведенными к данным плоскостям из произвольной точки пространства. В плоскости этих перпендикуляров получаем два угла, которые соответственно равны линейным углам двух смежных двугранных углов (рис.5.8б).
Задача 11. Величина плоской фигуры определяется методом замены плоскостей проекций, последовательным решением 3 и 4 основных задач. Плоскость преобразуется первоначально в проецирующую, относительно плоскостей проекций, а затем в плоскость уровня.
Вопросы для самоконтроля:
1) Опишите все группы метрических задач.
2) Опишите алгоритм преобразования чертежа для нахождения кратчайшего расстояния между скрещивающимися прямыми общего положения.
3) Опишите алгоритм преобразования чертежа для нахождения (измерения) углов треугольника, занимающего общее положение.
Позиционные задачи
