Вычисление широты по длине дуги меридиана
Поставим задачу, обратную только что решённой: найти широту по заданной длине дуги меридиана. Эта задача решается методом обращения тригонометрических рядов.
Формулы обращения тригонометрических рядов:
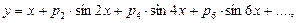 |
(82)
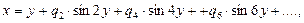 (83)
(83)
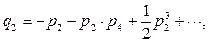 |
(84)
 |
(85)
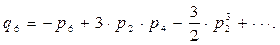 |
(86)
- 32 -
Найдя численные значения коэффициентов по элементам эллипсоида Красовского, получим ряд для вычисления широты в радианах в следующем виде:
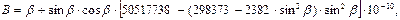 (87)
(87)
 где
где
(88)
Погрешность результата вычислений по формуле (87) не превосходит

и соответствует точности вычислений по формуле (80).
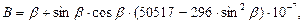 При пониженных требованиях к точности применяют более простую формулу
При пониженных требованиях к точности применяют более простую формулу
(89)
по которой значение широты определяется погрешностью, выраженной в градусной мере, менее 0,005".
Вычисление длины дуги параллели
Параллель на эллипсоиде является окружностью, поэтому вычисление длины дуги параллели сводится к определению длины дуги окружности ∆Y с центральным углом, равным разности долгот l =∆L = L2 - L1 конечных точек дуги.

Рис. 21. Длина дуги параллели
- 33 -
Радиус параллели r определяется формулой
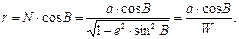 |
(90)
Длина дуги параллели ∆Y, имеющей широту В и разность долгот l конечных точек, определяется формулой
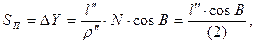 |
(91)
где


- радиан в секундах дуги.
Значение радиуса кривизны первого вертикала вычисляется по формуле
(92)

Отсюда легко получить формулу вычисления разности долгот l двух точек параллели на широте В.
 |
(93)
Для контроля вычислений длину дуги параллели следует определить, как разность длин дуг Y2 и Y1, отсчитываемых от меридиана с долготой L1 - 30' (рис. 21). Значения величин Y2 и Y1 получим, применяя формулу (91):
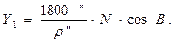 | |||
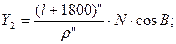 | |||
Искомую длину дуги параллели получим по формуле
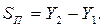 |
Примечание. Точность формулы (91) зависит от разности долгот l. Если l < 1°, то длину дуги параллели получим с ошибкой ± 0,001 м.
- 34 -
Примеры
Вычисления длин линий и площадей фигур на поверхности эллипсоида
Пример 1. Вычисление длины дуги меридиана между двумя точками с широтами В2 = 49°29'58,938'' и B1 = 45°30'17,221'', пользуясь формулой Симпсона
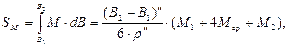 |
(94)
где:
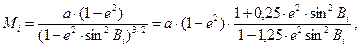
(95)
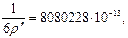 |
В1 и В2 - широты концов дуги меридиана; М1, М2, Мср - значения радиусов кривизны меридиана в точках с данными широтами и с широтой
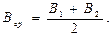 |
(96)
Для контроля вычислений длину дуги меридиана SМ следует вычислить как сумму длин дуг Х1 и Х2 меридиана от точки с широтой Вср до точек с широтами В1 и В2. На основании (93) будем иметь (рис. 21)
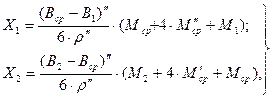 |
(97)
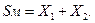 |
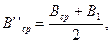
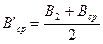 где M'ср и M''ср - значения радиусов кривизны меридиана в точках с широтами
где M'ср и M''ср - значения радиусов кривизны меридиана в точках с широтами
и которые
определяются по формуле (94).
- 35 -
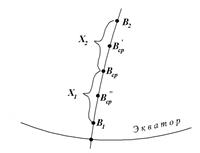 |
Рис. 21. Вычисление длины дуги меридиана
Примечание. При расстояниях между точками до 500 км формула (93) обеспечивает точность вычислений 1 - 2 см. Если дуга меридиана превышает 500 км, то для вычисления длины дуги следует разделить её на части, не превышающие 500 км, и применить формулу (93) к каждой части в отдельности.
Таблица 1
Вычисление длины дуги меридиана между двумя точками по формулам Симпсона
Схема решения
| Формулы | Результаты вычислений | Формулы | Результаты вычислений |
| a e2 | 6 378 245,0 м 0,006 693 42 | a e2 | 6 378 245,0 м 0,006 693 42 |
| a(1-e2) | 633 5552,717 м | 1,25e2sin2 B1 | 0,004 257 10 |
| 1/6 ρ" | 8 080 228·10-13 | 1,25e2sin2 B2 | 0,004 837 77 |
| B2 | 49°29'58,938" | 1,25e2sin2 Bср. | 0,004 548 32 |
| B1 | 45°30'17,221" | 1+0,25e2 sin2 B1 | 1,000 851 42 |
| Bср. | 47 30 08,080 | 1+0,25e2 sin2 B2 | 1,000 967 56 |
| 0,25e2 | 0,001 673 36 | 1+0,25e2 sin2 Bср. | 1,000 909 66 |
| 1,25e2 | 0,008 366 78 | 1 - 1,25e2 sin2 B1 | 0,995 742 90 |
| sinB1 | 0,713 308 97 | 1 - 1,25e2 sin2 B2 | 0,995 162 23 |
| sinB2 | 0,760 402 63 | 1 - 1,25e2sin2 Bср. | 0,995 451 68 |
| sinBср. | 0,737 303 80 | M1 | 6 368 056,324 м |
| sin2 B1 | 0,508 809 69 | M2 | 6 372 511,409 м |
| sin2 B2 | 0,578 212 16 | Mср. | 6 370 290,021 м |
| sin2 Bср. | 0,543 616 89 | (B2 - B1)" | 14 381,717" |
| 0,25e2 sin2 B1 | 0,000 851 42 | (B2 - B1)"/6 ρ" | 0,011 620 755 |
| 0,25e2 sin2 B2 | 0,000 967 56 | S, м | 444 165,343 м |
| 0,25e2 sin2 Bср. | 0,000 909 66 |
- 36 -
Таблица 2
