Умножение обыкновенной дроби на дробь.

Чтобы перемножить обыкновенные дроби, необходимо умножить числитель на числитель (получим числительпроизведения) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей: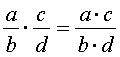

Например:

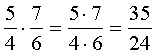
Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможностьсокращения дроби. Если получится сократить дробь, то вам легче будет дальше производить расчеты.

Обратите внимание! Здесь не нужно искать общий знаменатель!!

Деление обыкновенной дроби на дробь.

Деление обыкновенной дроби на дробь происходит так: переворачиваете вторую дробь (т.е. меняете числитель и знаменатель местами) и после этого дроби перемножаются.

Формула деления обыкновенных дробей:

1. Биссектриса угла

Биссектрисой является геометрическое место точек, равноудаленное от сторон угла.

Если говорить проще, то биссектриса – это линия, разделяющая угол пополам.

Биссектрисой угла - луч, выходящий из вершины угла и делящий его на два других равных угла.

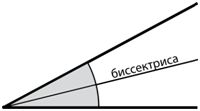
Слово «биссектриса» в переводе с французского языка обозначает, как надвое рассекающая или равноделящая угол пополам.

Билет №16

1. Деление десятичной дроби на десятичную дробь\

Чтобы разделить одну десятичную дробь на другую, переносим запятую вправо и в делимом, и в делителе на столько знаков, сколько их в делителе после запятой, то есть на три знака. Таким образом, 0,1218 : 0,058 = 121,8 : 58. Деление на десятичную дробь заменили делением на натуральное число. Делим уголком. Имеем: 0,1218 : 0,058 = 121,8 : 58 = 2,1.

1. Треугольник

Треугольник -это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки - его сторонами.

Сумма всех углов в треугольнике равна 180°.

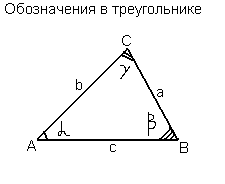
Вершины треугольника обычно обозначаются заглавными латинскими буквами (A, B, C), величины углов при соответственных вершинах — греческими буквами (α, β, γ), а длины противоположных сторон — прописными латинскими буквами (a, b, c).

Виды треугольников:

(по величине углов)

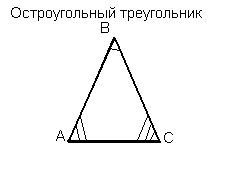
Остроугольный треугольник - это треугольник, в котором все три угла острые, т.е. меньше 90°.

Прямоугольный треугольник - это треугольник, содержащий прямой угол.

Две стороны, образующие прямой угол, называются катетами (АС и АВ), а сторона, противолежащая прямому углу, называется гипотенузой (ВС).

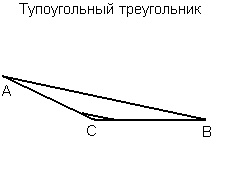
Тупоугольный треугольник - это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°.

(по числу равных сторон)

Равносторонний (правильный) треугольник - это треугольник, у которого все стороны и все углы равны (каждый угол равен 60°).

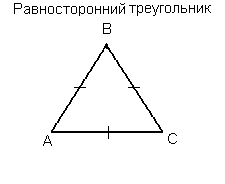
Равнобедренный тругольник - это треугольник, у которого два угла и две стороны равны.

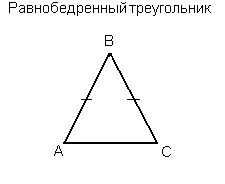
Основные свойства треугольников. В любом треугольнике:

Против большей стороны лежит больший угол, и наоборот.